 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
КОРРЕЛЯЦИЯ
Согласование в системе из двух наборов случайных величин  и
и  может быть обнаружено в рамках корреляционного анализа, в основе которого лежит гипотеза о связи между двумя признаками. Один из признаков – факторный (условно определяющий), а другой – результативный.
может быть обнаружено в рамках корреляционного анализа, в основе которого лежит гипотеза о связи между двумя признаками. Один из признаков – факторный (условно определяющий), а другой – результативный.
Проведенная прямая называется прямой регрессии или прямой, построенной методом наименьших квадратов. Последний термин связан с тем, что сумма квадратов расстояний (вычисленных по оси Y) от наблюдаемых точек до прямой является минимальной. Заметим, что использование квадратов расстояний приводит к тому, что оценки параметров прямой сильно реагируют на выбросы.
Регрессионный анализ заключается в определении аналитического выражения связи зависимой случайной величины Y (называемой результативным признаком) с независимыми случайными величинами X1, X2, …, Xm (называемые факторами).
Форма связи результативного признака Y с факторами X1, X2, …, Xm получила название уравнения регрессии.
Различают регрессии:
ü линейную и нелинейную (квадратичная, экспоненциальная, логарифмическая и т.д.),
ü парную и множественную (многофакторную) регрессии.
Исследования изменений статистических показателей с течением времени приводят к статистическим закономерностям, выраженным в виде рядов динамики.
Так, например, результатом таких исследований, проведенных органами статистики, явилась таблица, касающаяся динамики среднемесячной заработной платы в России за 1995 год. Проведение подобных исследований за последующие годы может определить тенденцию развития страны.
Аналогично можно использовать ряды динамики не только в макроэкономике, но и по отношению к небольшим предприятиям и организациям. На рисунке представлен ряд динамики выпуска продукции (в денежном выражении) некоторым предприятием. Скачкообразный характер распределения переменной (млн. руб.) во времени не позволяет сразу оценить тенденцию развития предприятия. Для определения закономерности в работе (стабильности, повышения или снижения показателей, ритмичности и т.п.) используется метод выравнивания ряда динамики, основанный на усреднении данных по укрупненным интервалам. Ряд, построенный по средним значениям в укрупненных интервалах, будет характеризоваться меньшей «колеблемостью» (флуктуациями) признака.
Таким образом, имеется средняя линяя развития – линия тренда. Скорость роста характеризуется коэффициентом роста, то есть тангенсом угла наклона линии тренда к оси времени.
 В практике статистического изучения временных рядов различают следующие основные типы развития явлений во времени:
В практике статистического изучения временных рядов различают следующие основные типы развития явлений во времени:
1. Равномерное развитие
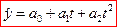 2. Равноускоренное (равнозамедленное) развитие
2. Равноускоренное (равнозамедленное) развитие
 |
3. Развитие с переменным ускорение (замедлением)
 4. Развитие с замедлением роста в конце периода
4. Развитие с замедлением роста в конце периода
Трендовыми моделями можно пользоваться для краткосрочных и среднесрочных прогнозов.
Поиск по сайту: