 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
I. ОСНОВЫ МОЛЕКУЛЯРНОЙ СТАТИСТИКИ 3 страница

Определения вероятности (2.3) и (2.14) совершенно эквивалентны. При решении задач следует выбирать наиболее удобное из них для конкретных условий.
Статистические постулаты
Молекулярная статистика как научная теория опирается на два основополагающих допущения, не имеющих в настоящее время доказательств, и поэтому называемых постулатами. Несмотря на это все последующие положения, законы, следствия и выводы теории имеют строгие логические доказательства и экспериментальные подтверждения.
Постулаты имеют свои исторически сложившиеся названия. Первый кратко именуют постулатом равновероятности. Второй постулат называют эргодической гипотезой.
Прежде всего, дадим развернутые (двухчастные) формулировки этих постулатов (см. схему 2.4.1), а затем прокомментируем их содержания.
Комментарий к постулату равновероятности
Как можно экспериментально установить, что система находится в равновесии? Для этого надо убедиться в том, что все наблюдаемые макроскопические параметры системы не зависят от времени. Рассмотрим микроканонический ансамбль систем.
Для любой частицы, входящей в каждую систему ансамбля, нет никаких предпочтений для нахождения в какой либо конкретной ячейке пространства по сравнению с другой. Все ячейки физически эквивалентны, все местоположения частицы равновозможны. Вследствие этого, системы статистического ансамбля в некоторый момент времени будут равномерно распределены по всем доступным микроскопическим состояниям.
С течением времени каждая система будет совершать переходы между различными доступными состояниями. Законы механики позволяют доказать, что такой динамический процесс не может изменить равномерное распределение систем по микросостояниям.
Равномерное распределение остается, таким образом, неизменным во времени. Другими словами, вероятность нахождения системы в каждом из доступных состояний не зависит от времени. Это стационарное состояние изолированной системы по определению является равновесным. При этом среднее значение любого измеряемого макроскопического параметра системы не будет зависеть от времени.
Обратите внимание на вторую часть постулата. В ней заключено предупреждение о возможности обнаружить изолированную систему в неравновесном состоянии. Однако, благодаря своей изолированности система обречена в обозримом будущем оказаться в равновесии.
Схема 2.4.1.
Эргодическая гипотеза:
І. Начиная свое движение из любого возможного микроскопического состояния, статистическая система обязательно достигнет состояния, сколь угодно близкого к любому другому состоянию, совместимому с пространственными ограничениями и с законом сохранения энергии.
ІІ. Вероятность по ансамблю равна вероятности по времени:
 Среднее по ансамблю равно среднему по времени:
Среднее по ансамблю равно среднему по времени:

|
| Постулат равновероятности доступных микроскопических состояний изолированной системы в состоянии термодинамического равновесия: І. Если изолированная статистическая система находится в состоянии термодинамического равновесия, то все доступные ей микроскопические состояния равновероятны. ІІ. Если микроскопические состояния изолированной статистической системы не равновероятны, то система не находится в состоянии термодинамического равновесия, но на пути к нему. |
| Статистические постулаты |
Комментарий к эргодической гипотезе
В первой части гипотезы постулируется (предполагается) свойство статистической системы, которое собственно и называется эргодичностью. Вторая часть формулировки является следствием первой части и решает вопрос об усреднении микроскопических параметров.
Микроскопические параметры, характеризующие отдельные молекулы системы, постоянно меняются во времени случайным образом. Можно ли рассчитать средние значения этих параметров с помощью применения формальной процедуры? В качестве примера рассмотрим усреднение квадрата координаты определенной частицы,  . По определению среднего по времени следует записать:
. По определению среднего по времени следует записать:

Изменение координаты будем рассматривать как результат перехода частицы из одной ячейки конфигурационного пространства в другую:

где  – число скачков в течении времени
– число скачков в течении времени 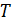 :
:

При  частица много раз попадает в каждую ячейку, за время
частица много раз попадает в каждую ячейку, за время 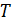 в -ой ячейке она проведет время
в -ой ячейке она проведет время
 , где сумма берется по всем
, где сумма берется по всем 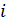 , соответствующим i -ой ячейке;
, соответствующим i -ой ячейке;
 ; с учетом вышеизложенного
; с учетом вышеизложенного

 – это выражение формально определяет вероятность по времени. Однако рассчитать эту вероятность невозможно, поскольку невозможно хронометрировать «судьбу» незримой частицы. Возникают вопросы:
– это выражение формально определяет вероятность по времени. Однако рассчитать эту вероятность невозможно, поскольку невозможно хронометрировать «судьбу» незримой частицы. Возникают вопросы:
• Равна ли вероятность по времени вероятности по ансамблю?
• Допустимо ли заменить «невозможную» процедуру усреднения по времени на процедуру усреднения по ансамблю?
Эргодическая гипотеза отвечает на эти вопросы утвердительно.
Впервые гипотеза была высказана в 1871г. Л.Больцманом, затем Дж.Максвелл в 1879г. проанализировал возможность замены средних по времени средними по ансамблю.
Вероятность макроскопического состояния
Если известны признаки интересующего нас макроскопического состояния системы (обозначим их 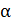 ), то можно, в принципе, зафиксировать и подсчитать все микросостояния
), то можно, в принципе, зафиксировать и подсчитать все микросостояния  , совместимые с этими признаками. Пусть
, совместимые с этими признаками. Пусть  общее число микроскопических состояний, доступных системе в соответствии с эргодической гипотезой. Тогда, исходя из постулата равновероятности микросостояний, согласно (2.3) получим формулу для вероятности макроскопического состояния
общее число микроскопических состояний, доступных системе в соответствии с эргодической гипотезой. Тогда, исходя из постулата равновероятности микросостояний, согласно (2.3) получим формулу для вероятности макроскопического состояния
 ,
, 
Число микроскопических состояний  , приводящее к данному макроскопическому состоянию, называется термодинамической вероятностью макросостояния. Задачей теории является нахождение
, приводящее к данному макроскопическому состоянию, называется термодинамической вероятностью макросостояния. Задачей теории является нахождение  и
и  , желательно не пересчитывая их. Лучшим вариантом, конечно было бы нахождение сразу вероятности
, желательно не пересчитывая их. Лучшим вариантом, конечно было бы нахождение сразу вероятности  , не зная
, не зная  и
и  и это порой возможно. Для этого существуют особые математические приемы. Некоторые из них мы рассмотрим в последующем.
и это порой возможно. Для этого существуют особые математические приемы. Некоторые из них мы рассмотрим в последующем.
Контрольные вопросы
1. Какие молекулярные системы называются идеальными? Приведите примеры.
2. Опишите модель системы идеальных спинов. Чему равно количество проекций спина на выделенное направление?
3. Что называется случайным событием? Дайте определения различным видам случайных событий.
4. Как определяется вероятность случайного события? В чем различие классического и статистического определений вероятности?
5. Что называется случайной величиной? Назовите основные числовые характеристики случайной величины. Запишите формулы для их нахождения.
6. Что называется плотностью вероятности? Запишите для нее условие нормировки.
7. Сформулируйте две теоремы теории вероятностей рассмотренных на лекции. Какая из них лежит в основе условия нормировки вероятности? Дайте математическое обоснование.
8. Что называется микроскопическим состоянием системы? Какие параметры используются для его описания в классических и квантовых системах?
9. Что называется микроканоническим статистическим ансамблем?
10. Как определяется вероятность микроскопического состояния по ансамблю и по времени?
11. Сформулируйте статистические постулаты. Поясните их смысл.
12. Дайте определение вероятности макроскопического состояния статистической системы?
ЛЕКЦИЯ 3
БИНОМИАЛЬНОЕ РАСПРЕДЕЛЕНИЕ И ЕГО ПРЕДЕЛЬНЫЕ СЛУЧАИ В ОПИСАНИИ МОЛЕКУЛЯРНЫХ СИСТЕМ
При описании статистических систем нас, конечно же, интересует пространственное распределение частиц. Наличие каких-либо силовых полей или их отсутствие определяет различные законы распределения вероятностей. Начнем исследование с простейшего случая – равновесного пространственного распределения частиц классического идеального газа в отсутствии силовых полей. Наша задача получить закон распределения вероятностей на основе базового определения вероятности макроскопического состояния изолированной системы (2.15).
3.1. Вывод закона распределения вероятностей
Описание системы
Рассмотрим изолированную систему, представляющую классический идеальный газ (рис. 3.1). Введем обозначения:
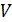 – объем, занимаемый газом; n –число частиц, находящихся в нем;
– объем, занимаемый газом; n –число частиц, находящихся в нем;
 – число ячеек, которые могут занимать частицы
– число ячеек, которые могут занимать частицы  ;
;
 некоторый фиксированный объем, часть
некоторый фиксированный объем, часть  ,
,  – число ячеек в объеме
– число ячеек в объеме  . Говоря об объеме
. Говоря об объеме  , мы имеем в виду
, мы имеем в виду

|
| Рис. 3.1. |
мысленно выделенное подпространство, не имеющее материальных границ (Рис. 3.1), поэтому в объеме V1 может находиться случайное число частиц  . Применение модели классического идеального газа требует выполнения условий:
. Применение модели классического идеального газа требует выполнения условий:  .
.
Актуальные свойства модели системы
• Пространство, занимаемое газом однородно и изотропно (нет выделенных мест и направлений).
• Частицы отличимы друг от друга (например, пронумерованы).
Последнее неожиданное допущение фиксирует факт отсутствия пространственной конкуренции между молекулами классического идеального газа 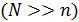 . Предположение о различимости частиц означает, что два микросостояния, в которых частицами заняты одни и те же ячейки, различны, если, например, две частицы поменялись местами в каких-то ячейках.
. Предположение о различимости частиц означает, что два микросостояния, в которых частицами заняты одни и те же ячейки, различны, если, например, две частицы поменялись местами в каких-то ячейках.
Следует обратить внимание на то, что рассматриваемые частицы совершенно одинаковы, поэтому свойства двух микросостояний, в которых частицы обменялись местами, должны быть абсолютно идентичными. Однако, мы считаем эти микросостояния различными, поскольку системе требуется определенное время для того, чтобы пройти эти «одинаковые» микросостояния. Различимость частиц в дальнейшем заставит нас выбрать «нужные» формулы комбинаторики для подсчета числа микросостояний системы.
Постановка задачи
Какова вероятность  макроскопического состояния системы, при котором в объеме
макроскопического состояния системы, при котором в объеме  находится
находится  частиц?
частиц?
Вывод закона
• По определению вероятность макроскопического состояния системы 
• Полное число микросостояний  рассчитаем, как число размещений
рассчитаем, как число размещений 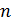 различимых частиц по
различимых частиц по 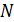 ячейкам
ячейкам  .
.
• Число размещений  частиц в объеме
частиц в объеме  по
по 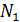 ячейкам:
ячейкам:

• Число состояний, доступных для остальных  частиц в объеме
частиц в объеме 

Каждое из микросостояний 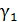
комбинирует со всеми микросостояниями  в силу их независимости
в силу их независимости
 .
.
• Поскольку частицы различимы, то фиксированное число молекул  , определяющее макросостояние, можно выбрать не одним способом. Количество способов – это число сочетаний, которыми можно выбрать
, определяющее макросостояние, можно выбрать не одним способом. Количество способов – это число сочетаний, которыми можно выбрать  различных частиц из
различных частиц из 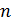 различных частиц
различных частиц

• Окончательно  – общее число микросостояний, посредством которых реализуется интересующее нас макросостояние.
– общее число микросостояний, посредством которых реализуется интересующее нас макросостояние.
Ответ:

Трудно представить, что такая громоздкая формула может найти хоть какое-нибудь применение.
Будем работать дальше в надежде на  .
.
Математические преобразования больших чисел.
Введение общепринятых обозначений
Для преобразования больших чисел обычно используют формулу Стирлинга.
Формула Стирлинга
 или или  при условии, что
при условии, что  . .
|
Эта формула позволяет существенно упростить (3.1), а именно

Введём общепринятые обозначения:
 – вероятность нахождения частицы в
– вероятность нахождения частицы в  ,
,
 – вероятность нахождения частицы в остальной части объёма,
– вероятность нахождения частицы в остальной части объёма,

– условие нормировки одночастичной вероятности.
Формула для вероятности макросостояния.
Закон Бернулли, или биномиальное распределение.
Используя общепринятые обозначения, представим (3.2) в виде

Это и есть окончательная формула для вероятности макросостояния.
Для полученного распределения выполняется условие нормировки вероятностей:

Это выражение совпадает с формулой бинома Ньютона.
В соответствии с (3.3)
 .
.
Следовательно

Благодаря связи с биномом Ньютона формула (3.4) получила свое распространенное название – биномиальное распределение. Другое название этого распределения – закон Бернулли, в честь ее автора известного европейского математика Якоба Бернулли. Заметим, что Бернулли получил выражение (3.4) иным способом, на основе теоремы умножения вероятностей независимых событий для любых значений 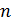 и
и  , не обязательно больших.
, не обязательно больших.
Биномиальное распределение справедливо для многих случайных событий, имеющих два возможных исхода. При этом обязательным условием выполнения закона является то, что вероятность реализации одного из исходов в единичном испытании должна быть постоянной  .
.
Биномиальное распределение отвечает на вопрос: какова вероятность осуществления  определённых исходов в
определённых исходов в 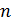 независимых испытаниях при известном значении
независимых испытаниях при известном значении 
Приведём примеры.
Какова вероятность того, что из 50 новорождённых 20 мальчиков? Какова вероятность того, что из 1000 новых одинаковых приборов на складе 5 бракованных?
В первом случае вероятность  приближенно можно считать равной
приближенно можно считать равной 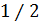 , а в последнем – постоянное значение
, а в последнем – постоянное значение  определяется уровнем технологии производства данных приборов (обычно
определяется уровнем технологии производства данных приборов (обычно  ).
).
3.2. Графическое представление биномиального распределения.
Графические представления биномиального распределения для разных значений n и p приведены на рис. 3.2:  ; б)
; б)  ; в) n
; в) n  ,
,  ,
,  ; г) г)
; г) г)  ,
,  ,
,  .
.

а


| б | в |

г
Рис. 3.2.
В предельном случае, когда  ,
,  , гистограмма переходит в непрерывную кривую в форме симметричного колокольчика (рис. 3.2, б).
, гистограмма переходит в непрерывную кривую в форме симметричного колокольчика (рис. 3.2, б).
Основные характеристики биномиального распределении.
Важными числовыми характеристиками распределения вероятностей являются наиболее вероятное значение числа частиц  , среднее значение
, среднее значение  , дисперсия и ряд других связанных с ними параметров. Формулы нахождения этих величин в зависимости от
, дисперсия и ряд других связанных с ними параметров. Формулы нахождения этих величин в зависимости от  приведены на схеме 3.2.1.
приведены на схеме 3.2.1.
Схема 3.2.1.
Cреднее значение m, 
|
Максимальное значение вероятности  отвечает условию отвечает условию
 Решение этого уравнения:
Решение этого уравнения:
 . .
|
 - среднее значение;
- среднее значение;
 . .
|
Наиболее вероятное значение 
|
Дисперсия, как мера флуктуации 
|
| Наиболее вероятная концентрация частиц в объеме V1 |
Относительное стандартное отклонение 
|

 ; ;  .
Если .
Если  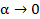 то.
Если то.
Если  , ,

|

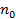 – концентрация, соответствующая равномерному распределению частиц по всему объему. – концентрация, соответствующая равномерному распределению частиц по всему объему.
|
| Характеристики биномиального распределении |


 – характеризует абсолютную растянутость графических кривых (ширину «колокольчика», см.рис. 2)
Если – характеризует абсолютную растянутость графических кривых (ширину «колокольчика», см.рис. 2)
Если  , а , а  тогда тогда  , следовательно , следовательно

|
Относительные флуктуации числа частиц в пространстве возрастают с уменьшением области, в которой эти флуктуации рассматриваются. В макроскопических системах флуктуации незначительны, поэтому можно считать, что  .
.
3.3. Предельные случаи биномиального распределения
В теории вероятностей анализ предельных форм биномиального распределения базируется на строгих доказательствах. Этому вопросу посвящены специальные теоремы.
На схеме 3.3.1 приведены результаты этих доказательств, имеющие важное значение для описания статистических систем  ).
).
Схема 3.3.1.
| Предельные случаи биномиального распределения |
Распределение Пуассона(закон редких событий):  . . 
 – вероятность редких событий (см. рис. 3.2, в, г), – вероятность редких событий (см. рис. 3.2, в, г),
 .
Например: технические катастрофы, биологические мутации, вылет частиц при радиоактивном распаде ядра, эффузия – молекулярное истечение газа из сосуда через небольшое отверстие в тонкой стенке. .
Например: технические катастрофы, биологические мутации, вылет частиц при радиоактивном распаде ядра, эффузия – молекулярное истечение газа из сосуда через небольшое отверстие в тонкой стенке.
|
Распределение Гаусса(нормальное распределение):  , ,   – распределение плотности вероятности, где m непрерывно изменяющаяся величина( – распределение плотности вероятности, где m непрерывно изменяющаяся величина( ) (см. рис. 3.2, б)).
Например: распределение молекул по компонентам скорости в состоянии теплового равновесия, распределение попаданий в мишень (прицельная стрельба), закон ошибок в метрологии. ) (см. рис. 3.2, б)).
Например: распределение молекул по компонентам скорости в состоянии теплового равновесия, распределение попаданий в мишень (прицельная стрельба), закон ошибок в метрологии.
|
В предельных случаях биномиальное распределение приобретает более простую математическую структуру. При решении конкретных задач, полезно, прежде всего, установить, относится ли рассматриваемая ситуация к какому-либо предельному случаю. Если относится, то следует применить соответствующую формулу, что значительно упростит решение.
Среди примеров, относящихся к области применимости распределения Пуассона, особое внимание обратим на явление эффузии. Это явление заключается в следующем.
Газ, находящийся в сосуде при низком давлении  , меленно истекает в окружающее сосуд разряженное пространство через отверстие, размеры которого много меньше средней длины свободного пробега молекул
, меленно истекает в окружающее сосуд разряженное пространство через отверстие, размеры которого много меньше средней длины свободного пробега молекул  . Параметр
. Параметр  равен среднему расстоянию, которое проходит молекула между двумя последовательными столкновениями. Количество частиц
равен среднему расстоянию, которое проходит молекула между двумя последовательными столкновениями. Количество частиц  , покидающих сосуд за малый интервал времени
, покидающих сосуд за малый интервал времени 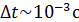 , является случайной величиной, подчиняющейся закону редких событий
, является случайной величиной, подчиняющейся закону редких событий  . В дальнейшем мы рассмотрим различные аспекты этого процесса, включая возможности его практического применения в экспериментальных исследованиях.
. В дальнейшем мы рассмотрим различные аспекты этого процесса, включая возможности его практического применения в экспериментальных исследованиях.
Поиск по сайту: