Продолжение 53

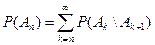сходится, т.к. слагаемые меньше 1, Þ предел его остатка равен 0: .

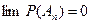Примеры моделей, реализующих систему аксиом:

1. Дискретное вероятностное пространство:

W={w₁, w₂,…} – счетное множество. Рассмотрим последовательности чисел P₁, …,P_n, P_k³0: 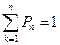. В качестве алгебры A рассмотрим совокупность всех подмножеств W и для любого АÎ А, А={w_i1, w_i2,…} по определению положим .

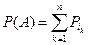Утверждаем, что так введенная определенная функция множеств Р является вероятностью.

Первые две аксиомы очевидны, а Р₃ является следствием свойства о перестановке слагаемых абсолютно сходящегося ряда.

Рассмотрим частный случай дискретного вероятностного пространства. W={w₁, w₂,…, w_n} состоит из конечного числа исходов, а соответствующие им числа P₁, …,P_n выберем одинаковыми, P₁, …,P_n=1. Тогда если А={w_i1, w_i2,…, w_ik} – некое событие из исходов, то .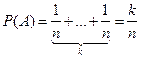

Данная вероятность называется классической. Применяется к случайным экспериментам с конечным числом равновозможных исходов. Вероятность отдельного исхода w_i равна 1/n.

Пример: Подбрасываются две игральные кости. Какова вероятность появления на верхних гранях одинакового числа очков?

Решение: естественно считать исходом пару чисел (i,j), i,j = 1…6. A={(1,1),(2,2),…,(6,6)} P(A)= .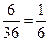

Поиск по сайту: