АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Частные производные функции двух переменных

Читайте также:
  1. I Психологические принципы, задачи и функции социальной работы
  2. I. Деньги и их функции.
  3. I. Функции эндоплазматической сети.
  4. II. Основные задачи и функции
  5. II. Основные задачи и функции
  6. II. Разделы социологии: частные социальные науки
  7. III. Предмет, метод и функции философии.
  8. IV. Конструкция бент-функции
  9. Ms Excel: мастер функций. Логические функции.
  10. SALVATOR создает Знания-Образы, когнитивные имитационные модели сознания, расширяющие человеческие возможности и защитные функции.
  11. V2: ДЕ 29 - Введение в анализ. Предел функции на бесконечности
  12. V2: ДЕ 32 - Дифференциальное исчисление функции одной переменной. Производная

Частные и полные приращения функции двух переменных.

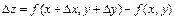- полное приращение;

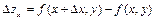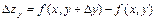и - частные приращения.

Частные производные функции двух переменных.

Частной производной по х от функции 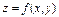называется производная, вычисленная в предположении, что у – постоянная. (производная по у вычисляется при постоянной х)

;

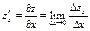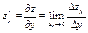
Частными производными второго порядка функции 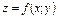называются частные производные от её частных производных первого порядка.

1) 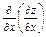= = 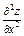= 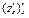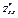; 2) = = =

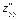
Смешанные производные: 3) 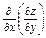= = 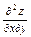= 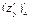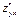; 4) = = =

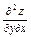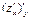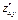
Если смешанные производные непрерывной функции двух переменных непрерывны, то они равны между собой. =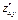

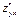
Определение локального экстремума функции двух переменных.

Функция 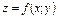имеет локальный максимум (минимум) в точке М0(х0,у0), если значении функции в этой точке больше (меньше), чем её значение в любой другой точке М(х,у) некоторой окрестности точки М0.

(точка. М0 – максимум, если 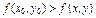для любых точек её окрестности.)

(Точка М0 – минимум, если 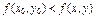для любых точек её окрестности.)


1 | 2 | 3 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.008 сек.)