 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Элементы теории. Метод золотого сечения — метод поиска значений действительно-значной функции на заданном отрезке
Метод золотого сечения — метод поиска значений действительно-значной функции на заданном отрезке. В основе метода лежит принцип деления в пропорциях золотого сечения. Наиболее широко известен как метод поиска экстремума в решении задач оптимизации.
Этот метод также относится к методам исключения интервалов. Он отличается от метода деления интервала пополам тем, что единичный интервал делится двумя пробными точками на три части (рис. 9.1). Каждая пробная точка отстоит от конца интервала на одну и ту же величину j [7]» 0,61803.
Пусть задана функция f (x): [ a, b ] → R, f (x) Î C ([ a, b ]). Тогда для того, чтобы найти определённое значение этой функции на заданном отрезке, отвечающее критерию поиска (пусть это будет минимум), рассматриваемый отрезок делится в пропорции золотого сечения в обоих направлениях, то есть выбираются две точки х (1) и x (2) такие, что:

Таким образом: 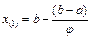 и
и 
То есть точка х (1) делит отрезок [ a, x (2)] в отношении золотого сечения. Аналогично x (2) делит отрезок [ x (1), b ] в той же пропорции. Это свойство и используется для построения итеративного процесса.

Рис. 9.1. Иллюстрация выбора промежуточных точек метода золотого сечения.
Алгоритм применения этого метода следующий:
- на первой итерации заданный отрезок делится двумя симметричными относительно его центра точками и рассчитываются значения в этих точках;
- после чего тот из концов отрезка, к которому среди двух вновь поставленных точек ближе оказалась та, значение в которой максимально (для случая поиска минимума), отбрасывают;
- на следующей итерации в силу показанного выше свойства золотого сечения уже надо искать всего одну новую точку;
- процедура продолжается до тех пор, пока не будет достигнута заданная точность.
1. Определим величину j = 0,61803×(b - a).
2. Определим х (1) = b - j; x (2) = a + j.
3. Подсчитаем значения f (х (1)) и f (x (2)).
4. Сравним f (х (1))и f (x (2)). Если f (х (1)) < f (x (2)), исключим интервал (x (2), b). Положим b = x (2). Определим L = b - a. Если L > λ, перейдем к п.1. Если L £ λ, решение найдено.
5. Если f (х (1)) > f (x (2)), исключаем интервал (а, х (1)). Положим а = х (1). Определим L = b - a. Если L > ɛ, перейдем к п.1. Если L £ λ, решение найдено.
6. Если f (х (1)) = f (x (2)), исключаем интервалы (a, х (1)) и (x (2), b). Положим а = х (1), b = x (2). Определим L = b - a. Если L > λ, перейдем к п.1. Если L £ ɛ, решение найдено.
Достоинством методов исключения интервалов является то, что они основаны лишь на вычислении значений функций. Не требуется, чтобы функции были дифференцируемыми, более того, допустимы случаи, когда функцию нельзя даже записать в аналитическом виде. Единственным требованием является возможность определения значений функции в заданных точках х с помощью прямых расчетов или имитационных экспериментов. Метод же золотого сечения выделяется среди методов исключения интервалов тем, что он требует наименьшего числа оцениваний значений функции для достижения одной и той же заданной точности.
Выполнение работы в среде MS EXCEL
Реализация этого метода в MS EXCEL аналогична реализации предыдущего метода. Исходными данными также служат определенные интервалы поиска и заданное значение точности поиска ɛ. Таблица расчетных данных должна содержать, согласно алгоритму расчета, графы расчета величин a, b, t, L, х (1), x (2), f (х (1)), f (x (2)). Все величины, кроме a и b, рассчитываются по приведенным в алгоритме формулам, а величины a и b – по формулам, содержащим логические функции EXCEL. При этом формулы, введенные на второй итерации, должны быть составлены таким образом, чтобы при копировании на последующие итерации они обеспечивали бы правильность расчета без редактирования. Расчет заканчивается на той итерации, для которой L < λ.
Пример выполнения представлен в табл. 9.1.
Таблица 9.1
f (x) = (100- x)2 λ= 0,1 j = 0,61803
| Итерация | a | b | τ | х (1) | x (2) | f (х (1)) | f (x (2)) | L |
| 65,000 | 185,000 | 74,164 | 110,836 | 139,164 | 117,417 | 1533,825 | 120,000 | |
| 65,000 | 139,164 | 45,836 | 93,328 | 110,836 | 44,513 | 117,417 | 74,164 | |
| 65,000 | 110,836 | 28,328 | 82,508 | 93,328 | 305,978 | 44,513 | 45,836 | |
| 82,508 | 110,836 | 17,508 | 93,328 | 100,016 | 44,513 | 0,000 | 28,328 | |
| 93,328 | 110,836 | 10,820 | 100,016 | 104,149 | 0,000 | 17,210 | 17,508 | |
| 93,328 | 104,149 | 6,687 | 97,461 | 100,016 | 6,446 | 0,000 | 10,820 | |
| 97,461 | 104,149 | 4,133 | 100,016 | 101,594 | 0,000 | 2,541 | 6,687 | |
| 97,461 | 101,594 | 2,554 | 99,040 | 100,016 | 0,922 | 0,000 | 4,133 | |
| 99,040 | 101,594 | 1,579 | 100,016 | 100,619 | 0,000 | 0,383 | 2,554 | |
| 99,040 | 100,619 | 0,976 | 99,643 | 100,016 | 0,128 | 0,000 | 1,579 | |
| 99,643 | 100,619 | 0,603 | 100,016 | 100,246 | 0,000 | 0,060 | 0,976 | |
| 99,643 | 100,246 | 0,373 | 99,873 | 100,016 | 0,016 | 0,000 | 0,603 | |
| 99,873 | 100,246 | 0,230 | 100,016 | 100,104 | 0,000 | 0,011 | 0,373 | |
| 99,873 | 100,104 | 0,142 | 99,961 | 100,016 | 0,002 | 0,000 | 0,230 | |
| 99,961 | 100,104 | 0,088 | 100,016 | 100,049 | 0,000 | 0,002 | 0,142 | |
| 99,961 | 100,049 | 0,054 | 99,995 | 100,016 | 0,000 | 0,000 | L<l |
Контрольные вопросы
1. Какой принцип лежит в основе метода золотого сечения?
2. Чем метод золотого сечения отличается от метода деления интервала пополам?
3. Чему равна пропорция золотого сечения?
4. Каков алгоритм применения метода золотого сечения?
5. Что является достоинством методов исключения интервалов?
6. Какое требование является единственным при применении метода золотого сечения?
7. В каких точках интервала сравниваются значения функции при использовании метода золотого сечения?
8. Чем метод золотого сечения выделяется среди методов исключения интервалов?
9. Что является исходными данными при реализация метода золотого сечения в MS EXCEL?
10. Каким образом должны быть составлены формулы введенные на второй итерации при реализация метода золотого сечения в MS EXCEL?
11. На какой итерации заканчивается расчет при реализация метода золотого сечения в MS EXCEL?
Поиск по сайту: