Формула Вульфа – Брегов

Направления, в которых получаются дифракционные максимумы, определяются условием, чтобы разность хода двух волн, отразившихся от соседних атомных слоев, была кратна l.

, (m =1, 2, …). (9.16)

Дифракция рентгеновских лучей от кристаллов используется для исследования спектрального состава рентгеновского излучения и для изучения структуры кристаллов. Наблюдение осуществляется с помощью фотопластинки.

Контрольные вопросы:

1. В чем отличие явления дифракции света от интерференции?

2. Позволяет ли принцип Гюйгенса рассчитать амплитуду результирующей волны в любой точке пространства?

3. В чем отличие дифракции Френеля от дифракции Фраунгофера?

4. С помощью какого прибора можно изучить спектральный состав излучения?

5. Рассчитайте амплитуду результирующей волны при дифракции Фраунгофера на круглом отверстии.

6. Как исследовать дифракцию рентгеновских волн?

ГЛАВА 10. Поляризация света

10.1. Поляризация света

10.2. Поляризация при отражении и преломлении света. Закон Брюстера. Степень поляризации

10.3. Поляризация при двойном лучепреломлении

10.4. ных источников. Опыт Юнга________________________________________________________________________________________________Анализ поляризации света. Закон Малюса

10.5. Поляризационные приборы: призма Николя, стопа Столетова, поляроидные пленки

10.6. Вращение плоскости поляризации. Искусственная оптическая анизотропия. Интерференция поляризованных лучей

10.1. Поляризация света

Поляризацией называется упорядоченное колебание вектора напряженности электрического поля Е или вектора напряженности магнитного поля Н в электромагнитной волне. Различают плоско поляризованные и эллиптически поляризованные волны.

Электромагнитная волна называется плоско поляризованной, если вектор Е колеблется в одной плоскости, называемой плоскостью поляризации. Перпендикулярная плоскость называется плоскостью колебаний (рис. 10.1).

Телевизионные передачи осуществляются с помощью поляризованных электромагнитных волн. Приемные антенны телевизоров располагаются в плоскости поляризации, т.е. в плоскости изменения вектора Е.

Если вектор Е при движении электромагнитной волны описывает эллипс, то электромагнитная волна называется эллиптически поляризованной (рис. 10.2).

Правая поляризация соответствует вращению вектора Е по часовой стрелке, если смотреть против направления распространения волны (рис. 10.3).

Левая поляризация соответствует вращению вектора Е против часовой стрелки.

Поляризация света является результатом сложения двух взаимно-перпендикулярных когерентных колебаний.

Рис. 10.1.

Рис. 10.2.

Рассмотрим колебания электрического вектора Е, являющегося результирующим вектором при сложении напряженностей и двух волн.

Если колебания происходят в одном направлении, то результирующая амплитуда в случае некогерентных волн:

.

Если волны когерентны, то результат сложения зависит от разности фаз волн d = j₂ - j₁ и возникает интерференция:

. (10.1)

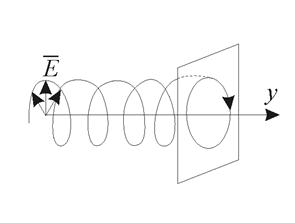
Рис. 10.3.

Пусть теперь электрические колебания взаимно перпендикулярны (рис. 10.4):

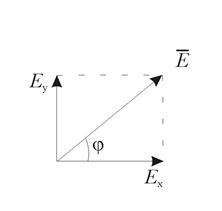
Рис. 10.4.

Результирующая напряженность является суммой векторов:

Е = Е _х + Е _y.

Тангенс угла j между направлениями векторов Е _х и Е _y.

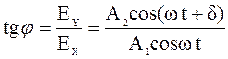. (10.2)

Результирующее колебание зависит от разности фаз d точно так же, как результат сложения двух механических взаимно перпендикулярных колебаний зависит от разности фаз.

1. Если 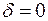, p, то находим:

= const. (10.3)

Результирующее колебание вектора Е совершается в фиксированном направлении. В этом случае волна является плоскополяризованной.

2. Если , то

. (10.4)

Угол между вектором Е и осью х изменяется со временем, конец вектора Е описывает эллипс, следовательно, световая волна является эллиптически поляризованной.

При A₁ = A₂ эллипс превращается в окружность – получается свет, поляризованный по кругу.

Две когерентные плоскополяризованные световые волны, плоскости колебаний которых взаимно перпендикулярны, при наложении друг на друга дают эллиптически поляризованную световую волну.

Естественный свет не обладает определенной поляризацией, так как электромагнитные волны, излучаемые источником света, колеблются в различных направлениях и с различной частотой.

Моделью естественного света является пучок электромагнитных волн, в котором некогерентные колебания происходят в двух взаимно перпендикулярных направлениях.

Поляризованный свет можно получить двумя способами: при отражении и преломлении света и при двойном лучепреломлении.

10.2. Поляризация при отражении и преломлении света. Закон Брюстера. Степень поляризации

При падении естественного света на прозрачный диэлектрик отраженная и преломленная волна является частично поляризованными.

Отраженная волна поляризована преимущественно в плоскости, перпендикулярной к плоскости падения, а преломленная – в плоскости падения (рис. 10.5).

Рис. 10.5.

Естественный свет можно представить в виде двух волн, плоско поляризованных во взаимно перпендикулярных плоскостях, одна из которых выбрана лежащей в плоскости падения, а другая перпендикулярна плоскости падения света.

Шотландский физик Д. Брюстер установил закон зависимости угла падения света, при котором отраженный свет полностью поляризован, от относительного показателя преломления .

Закон Брюстера

При падении под углом отраженный свет полностью поляризован, а преломленный свет частично поляризован с максимальной степенью поляризации.

. (10.5)

При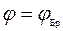

.

Степень поляризации света находится по формуле:

, (10.6)

где и - интенсивность света в плоскости падения и перпендикулярно плоскости падения.

Для определения степени поляризации отраженного света при :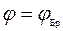

.

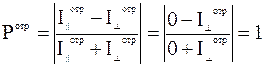Степень поляризации естественного света:

,

так как .

Степень поляризации преломленного света , при 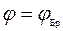она близка к 1.

Степень поляризации отраженного и преломленного лучей при различных углах падения света на диэлектриках можно получить с помощью формул Френеля.

Естественный свет можно представить в виде двух плоско поляризованных во взаимно-перпендикулярных направлениях волн. Выберем плоскости поляризации так, чтобы одна из них совпадала с плоскостью падения. Составляющие вектора напряженности электрического поля, лежащие в плоскости падения для падающей, отраженной и прошедшей волн обозначим: , соответственно.

Перпендикулярные к ним составляющие обозначим: . Каждая из шести составляющих имеет определенную интенсивность 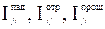и .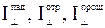

Коэффициенты отражения z и пропускания d для параллельной и перпендикулярной составляющих:

Равенство означает, что отраженный свет содержит только составляющую вектора Е в перпендикулярной плоскости падения, т.е. полностью поляризован. Это возможно при условии: , т.е. при .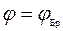

Для любого значения наряду с параллельной составляющей во вторую сферу проникает и перпендикулярная составляющая света.

Степень поляризации света, прошедшего во вторую среду:

.

Аналогично, в общем случае для степени поляризации отраженного света:

.

10.3. Поляризация при двойном лучепреломлении

Двойное лучепреломление происходит при прохождении света через кристаллы, не обладающие кубической решеткой. Это явление было открыто в 1670 г. монахом Бартолиусом и изучалось Х. Гюйгенсом и И. Ньютоном. Если посмотреть, например, на текст через такой кристалл, то получится двойное изображение. Такие кристаллы называются анизотропными, т.к. их оптические, а так же механические, тепловые и электрические свойства не одинаковы вдоль различных направлений.

Анизотропные кристаллы разделяются на одноосные и двуосные. Рассмотрим одноосные кристаллы, имеющие выделенное направление, вдоль которого обыкновенный и необыкновенный лучи проходят не разделяясь. Это направление называется оптической осью. Любая прямая, параллельная данному направлению, является оптической осью кристалла.

Плоскость, проходящая через оптическую ось, называется главной плоскостью кристалла.

Примером одноосного кристалла является исландский шпат, кварц, турмалин.

Обыкновенный и необыкновенный лучи полностью поляризованы, причем плоскость поляризации обыкновенного луча ^ к главному сечению, следовательно, его плоскость колебаний лежит в главной плоскости кристалла. Плоскость поляризации необыкновенного луча лежит в главной плоскости кристалла.

Луч в кристалле разделяется на два луча - обыкновенный и необыкновенный (рис. 10.6).

Рис. 10.6.

Луч, который подчиняется обычному закону преломления, называется обыкновенным.

Обыкновенный луч подчиняется обычному закону преломления . щием иевенно. ктрического поля______________________________________________________________________________________________Для другого луча, называемого необыкновенным, отношение и зависит от угла падения луча на кристалл. Это явление связано с различным значением диэлектрической проницаемости кристалла вдоль различных направлений в нем.

Обыкновенный и необыкновенный лучи распространяются в различных направлениях и с разными скоростями. Плоскость поляризации в обыкновенном луче перпендикулярна главной плоскости кристалла.

Главная плоскость кристалла проходит через направляющий вектор луча и главную оптическую ось кристалла.

Скорость обыкновенного луча во всех направлениях одинакова (рис. 10.7).

Рис. 10.7.

Скорость необыкновенного луча в направлениях 2 и 3 отличается от скорости в направлении главной оптической оси (рис. 10.8).

, .

где , - показатели преломления для обыкновенного и необыкновенного лучей.

В двуосном кристалле оба луча являются необыкновенными. Любая прямая, параллельная данному направлению, является оптической осью кристалла. Обыкновенный и необыкновенный лучи полностью поляризованы, причем плоскость поляризации обыкновенного луча ^ к главному сечению, следовательно, его плоскость колебания лежит в главной плоскости кристалла. Плоскость поляризации необыкновенного луча лежит в главной плоскости кристалла.

Рис. 10.8.

Объяснение двойного лучепреломления и поляризации света стало возможно только с помощью электромагнитной теории света Д. Максвелла.

Причина превращения естественного света в плоско поляризованный заключается в анизотропии оптической решетки, т.е. различном взаимном расположении атомов или ионов в разных направлениях кристалла.

В одноосных кристаллах диэлектрическая проницаемость зависит от направления - вдоль оптической оси и - в направлениях перпендикулярных к ней.

Скорость распространения света вдоль этих направлений так же различна. Для обыкновенного луча:

,

где , отсюда находим:

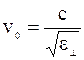. (10.7)

Для необыкновенного луча:

,

где 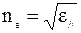, отсюда следует:

. (10.8)

Пусть источник света находится внутри кристалла. Волновой поверхностью обыкновенных лучей будет сфера.

Волновой поверхностью необыкновенных лучей будет эллипсоид вращения, т.к. колебания вектора Е в необыкновенном луче происходит в главной плоскости кристалла, причем вектор Е образует с оптической осью разные углы в зависимости от направления луча. Для луча 1 скорость , а для луча 2 скорость .

Поиск по сайту: