 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Закон Кирхгофа в интегральной форме для серых тел
При данной температуре сильнее излучают те серые тела, которые обладают большим коэффициентом поглощения:
 ,
,
где  - интегральная энергетическая светимость абсолютно черного тела;
- интегральная энергетическая светимость абсолютно черного тела;
А - коэффициент, учитывающий степень черноты тела.
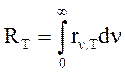 - интегральная энергетическая светимость реального тела.
- интегральная энергетическая светимость реального тела.
12.4. Закон Рэлея-Джинса. Формула Планка
Зависимость спектральной плотности энергетической светимости абсолютно черного тела от температуры и частоты была получена Рэлеем и Джинсом

 kT,
kT,
где  - число степеней свободы;
- число степеней свободы;
kT - средняя энергия, приходящаяся на одну колебательную степень свободы.
В области больших частот теоретические значения не соответствовали полученным экспериментальным результатам. Противоречие между существовавшими представлениями о характере теплового излучения и опытом было столь значительно, что получило название «ультрафиолетовой катастрофы».
М. Планк нашел выход из создавшегося противоречия. Он предположил, что атомы излучают и поглощают энергию дискретно. Энергия одного кванта излучения e = hn, где h - постоянная Планка, h = 6.62×10-32 Дж×с.
Формула Планка
 .
.
В формуле Планка, как и ранее, число степеней свободы системы было равно  , но средняя энергию осциллятора имела вид
, но средняя энергию осциллятора имела вид
 .
.
Планк Макс Карл Людвиг (1858 – 1947), немецкий физик – теоретик, основоположник квантовой теории. Родился в Киле. Окончил Мюнхенский университет.
Вывод формулы Планка
Фотоны являются частицами с целым спином, поэтому они подчиняются статистике Бозе-Эйнштейна, т.е. в элементе объема может быть сколько угодно фотонов данной частоты и поляризации. Совокупность таких фотонов, распространяющихся в данном направлении, называется квантовым осциллятором. Осциллятор может находиться в основном состоянии или в 1, 2, 3, и т.д. возбужденных состояниях.
Согласно каноническому распределению Гиббса, в условиях термодинамического равновесия вероятность P(n) нахождения осциллятора в n-ом возбужденном состоянии равна:
 ,
,
где а не зависит от n.
Полная вероятность обнаружить осциллятор в одном из состояний:

Среднее превышение энергии такого осциллятора над нулевой энергией

Формула Планка хорошо согласуется с результатами экспериментов во всем диапазоне частот и температур. При малых частотах формула Планка совпадает с формулой Рэлея-Джинса.
Если hn << kT, то
 ,
,
отсюда следует, что
 .
.
Из формулы Планка можно вывести закон Стефана-Больцмана:
 .
.
Сделаем замену переменных в интеграле:  , тогда
, тогда  и
и  .
.
Найдем интеграл:
 .
.
Получим закон Стефана-Больцмана:
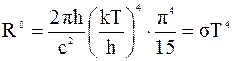 ,
,
где 
 .
.
Излучение нагретого тела, находящегося в равновесных условиях, может значительно отличаться от теплового.
Строго равновесное состояние может быть достигнуто, если тело помещено в оболочку, т.е. полость с непрозрачными стенками, температура которой 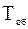 равна температуре тела
равна температуре тела  . Если
. Если 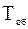 ¹
¹  , то излучение нельзя считать тепловым.
, то излучение нельзя считать тепловым.
12.5. Люминесценция и люминесцентный анализ
Поиск по сайту: