 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Черчение
1. Короев Ю. И. Строительное черчение и рисование.— М., 1983.
2. Строительное черчение и рисование / Б. В. Будасов, В. П. Каминский, Г. Б. Базилевский, В. В. Владиславский; Под ред. Б. В. Будасова. - М., 1981.
3. Федоренко В. А., Шошин А. Н. Справочник по машиностроительному черчению. - М., 1986.
4. Семенов В. Н. Унификация и стандартизация в проектной документации в строительстве. - Л., 1985.
5. Семенов В. Н., Тумаркин П. И. Состав и содержание строительных изделий // На стройках России. - 1985 - № 9, 10, 11; 1986 - № 2, 3, 5, 6, 7, 12; 1987 - №1.
6. Государственные стандарты ЕСКД. - М., 1984.
7. Государственные стандарты СПДС. - М., 1977 - 1988.
РАБОЧИЙ ПЛАН ИЗУЧЕНИЯ НАЧЕРТАТЕЛЬНОЙ ГЕОМЕТРИИ И ЧЕРЧЕНИЯ
| Номер | Наименование темы | Литература* | Контрольная работа | ||||
| условной недели | темы | [1] | [2] | лист | задача | неде-ля сдачи | |
| 1...7 2, 3 4,5 8... 16 9,10 11,12 17... 18, 19 20, 21 23,24 28, 29 33, 48 41, 42 43..45 46..48 | б 19. .1 .2 .3 .4 .5 | Контрольная работа 1 Начертательная геометрия Титульный лист и содержание Работа над ошибками Введение. Центральные и параллельные проекции Точка, прямая, плоскость в ортогональных проекциях Позиционные и метрические задачи Способы преобразования проекций Многогранники Контрольная работа 2 Кривые линии Поверхности Пересечение поверхности плоскостью и прямой Взаимное пересечение поверхностей Развертки поверхностей Плоскости касательные к поверхностям Аксонометрия. Основные положения и теоремы Проекции с числовыми отметками. Точка, прямая, плоскость Проекции с числовыми отметками. Поверхности. Контрольная работа 3 Титульный лист и содержание Работа над ошибками Тени в ортогональных и аксонометрических проекциях Перспектива и тени в перспективе Черчение Стандарты чертежей Геометрические построения: алгоритмизация геометрических построений сопряжения, уклоны Изображения: основные виды виды, разрезы, сечения оптимизация изображений аксонометрические проекции технический рисунок Контрольная работа 4 Титульный лист и содержание Работа над ошибками Разъемные и неразъемные соединения Чертежи машиностроительных изделий: деталировка сборочного чертежа эскиз детали Чертежи строительных изделий: спецификация строительного изделия сборочный чертеж строительного изделия рабочий чертеж строительной единицы рабочий чертеж детали Чертежи узлов строительных конструкций Контрольная работа 5 Строительные чертежи. Чертежи архитектурных решений здания: фасад план разрез с узлами конструкций | с. 5—8 § 4-16 § 17-24 § 28-35 § 25-27 § 37-39 § 40-48 § 49-50 § 51-54 § 57-58 § 55 § 60-65 § 74-78 § 79-81 § 82-90 § 71-73 § 1-7 § 8-12 § 15-23 81, 85-89 § 24-30 § 31-40 § 38-40 56-60 § 169 § 50-54 | Гл. 2, § 1, 2, 5 Гл. 3, § 1-15 Гл. 3, § 16-20 Гл. 3, §9 Гл. 7, § 1-4, 8 Гл. 6, § 1-7 Гл. 7 § 1-5 Гл. 8 § 1, 2 Гл. 10 § 1-3 Гл. 11 § 1-4 Гл. 12 § 6 Гл. 8 §3 Гл. 9 § 4-8 Гл. 10 §3 Гл. 9, § 9 Гл. 10 §3 Гл. 12 §2 Гл. 13 § 1-5 - Гл.14 § 3-9 Гл. 14 § 1-5 Гл. 14 § 6—8 Гл. 16 § 1-7, 9 Гл. 16 §8 § 4-10 § 11-14 § 15-22, § 2-35 § 36-49 § 71-75 § 76—81 § 51—69 | - - 1. 4, 5 4,5 б | 1, 2 - 1, 2 1,2,3 1, 2 1, 2 1, 2,3 1, 2 1, 2 - 1,2, 3, 1,2,3, 1, 2 1,. 2 1, 2 1...5 1...5 1,2 1,2 1,2 1,2 1,2,3 1,2,3 |
* В квадратных скобках указаны номера учебников. Номера учебников по начертательной геометрии и черчению совпадают.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ИЗУЧЕНИЮ НАЧЕРТАТЕЛЬНОЙ ГЕОМЕТРИИ
При изучении курса начертательной геометрии рекомендуется внимательно ознакомиться с программой, приобрести необходимую учебную литературу, организовать рабочее место и обратить особое внимание на рабочий план, который является первым помощником студентов я организации самостоятельного изучения курса, так как подсказывает, какую тему нужно изучить за неделю, какой проработать учебный материал и какое выполнить графическое задание. Правильно построенные самостоятельные занятия позволяют сэкономить время и получить хорошие результаты. При самостоятельной организации учебного процесса следует руководствоваться следующим:
1) изучать начертательную геометрию строго последовательно и систематически;
2) проработанные теоретические положения обязательно подкреплять практическим решением задач. С этой целью рекомендуется перерешать задачи на с. 46-52.
3) уделять серьезное внимание ответам на вопросы, предложенные данными методическими указаниями;
4) вместо механического конспектирования отдельных положений и примеров учебника рекомендуется письменно отвечать на вопросы курса, помещенные на с. 44-46, так как это приучает самостоятельно мыслить и кратко формулировать сущность изучаемых вопросов;
5) проявлять максимальную самостоятельность в занятиях, так как начертательную геометрию заучить нельзя, ее надо понимать;
6) научиться совмещать текст и чертеж книги, привлекая на помощь свое пространственное воображение, допуская в отдельных случаях простейшие модели;
7) приучить себя укладываться в сроки, рекомендуемые рабочим планом, и своевременно отсылать и передавать на рецензирование контрольные работы.
ПРИНЯТЫЕ ОБОЗНАЧЕНИЯ
1. Точки, расположенные в пространстве, - прописными буквами латинского алфавита А, В, С, D.. или цифрами 1, 2, 3, 4,...
2. Прямые и кривые линии в пространстве — строчными буквами латинского алфавита а, b, с, d,...
3. Плоскости - строчными буквами греческого алфавита a, β, γ, δ...
4, Поверхности - прописными буквами греческого алфавита Ф, Ө, Λ, Σ
5. Основные операции над геометрическими образами:
а) совпадение двух геометрических образов ≡, например a ≡ b, А1 ≡ В1;
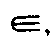
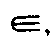
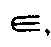б) взаимная принадлежность геометрических образов или, например а a, β В,
в) пересечение двух геометрических образов ∩, например t ∩ a, a ∩ β;
г) результат геометрической операции =, например К= а ∩a.
6. Способ задания геометрического образа указывается в скобках рядом с его буквенным обозначением, Например:
а(А, В) прямая задана двумя точками А и В;
a(А, В, С) ----плоскость задана тремя точками А, В и С;
β(а, А) — плоскость задана прямой а и точкой А;
γ(а ∩ b) — плоскость задана пересекающимися прямыми а и b;
γ(i ii m) —плоскость задана параллельными прямыми i и m.
7. Углы - строчными буквами греческого алфавита φ, ψ, ω.
Прямой угол обозначается точкой внутри сектора
8. Особые прямые и плоскости имеют постоянные обозначения:
а) линии уровня: горизонталь - h,
фронталь - f
б) следы плоскости обозначаются той же буквой, что и плоскость, с добавлением подстрочного индекса, соответствующего плоскости проекций;
в) линии уклона - u;
касательная прямая - t;
нормаль - n;
оси вращения — i, j.
9. Последовательность геометрических образов - надстрочным индексом:
точек - А1, А2, А3,
прямых - а1, а2, а3,
плоскостей - a1, a2, a3.
10. Центр проецирования - прописной буквой латинского алфавита S.
11. Направление проецирования - строчной буквой латинского алфавита s.
12. Плоскость проекций при образовании комплексного чертежа - прописной буквой греческого алфавита П:
горизонтальная - П1;
фронтальная - П2;
профильная — Пз.
13. Новая плоскость проекций при замене плоскостей проекций - буквой П с добавлением подстрочного индекса: П4, П5.
14. Проекции точек, прямых и плоскостей - соответствующей буквой с добавлением подстрочного индекса, характеризующего плоскость проекций:
на плоскости П1 — А1, а1, a1,
«» П2 — А2, а2, a2,
«» П3 — А3, а3, a3.
15. Оси проекций на комплексном чертеже — х12, y13, у31, z23...
16. Плоскость проекций при образовании моночертежа (в аксонометрии, в перспективе и в проекциях с числовыми отметками) - прописной буквой греческого алфавита с добавлением значка «штрих» - ПI.
17. Аксонометрические оси — хI, уI. zI, начало аксонометрических осей - ОI.
18. Аксонометрические и перспективные проекции точек, прямых и плоскостей - буквами, соответствующими натуре, с добавлением значка «штрих»: АI, аI, aI.
19. Вторичные проекции - с добавлением подстрочного индекса: АI1, АI2, АI3, аI1, аI2, аI3, aI1, aI2, aI3.
20. Аксонометрические единицы по осям -
21. Треугольник следов — ХI, УI, ZI.
22. Показатели искажения — u, v, ω.
23, Приведенные показатели искажения -- U, V, W.
24, Главная точка картины в перспективе - Р.
25. Линия горизонта - h
26. Основание картины — 0102.
27. Дистанционная точка - D.
28. Проекции точек в проекциях с числовыми отметками - той же буквой, что и натура, с добавлением числа, характеризующего расстояние точки до плоскости проекции, - А15, В-20, С0.
29. Масштаб уклона плоскости - той же буквой, что и плоскость, с добавлением индекса i; изображается двойной линией тонкой и жирной, разделенной на интервалы.
30. Масштабы уклонов плоскостей одинакового уклона, но различного положения к плоскости уровня -- одной буквой с добавлением подстрочного индекса: a1i, a2i, a3i, β1i, β2i, β3i, γ1i, γ2i, γ3i.
КОНТРОЛЬНАЯ РАБОТА 1
(Листы 1...6. Листы 2, 4, 6 выполняют на обороте листов 1, 3, 5)
Таблица 2
| номер варианта | ||||||||||
| номер задачи |
Лист 1
Формат АЗ. Выполняются титульный лист и содержание контрольных работ по рис. 1.
Лист 2
Формат АЗ. Основная надпись по форме 4б (см. рис. 2). Выполняются графические задания, связанные с допущенными ошибками в рецензируемых листах. Объем и характер задач определяются преподавателем.
Лист 3
Формат АЗ. Основная надпись по форме 4а. Выполняются две задачи по формализации процесса графического решения позиционных и метрических задач. Пример оформления листа на рис. 7. На примере показана задача 1, но в зависимости от варианта может быть 1, 2 или З.
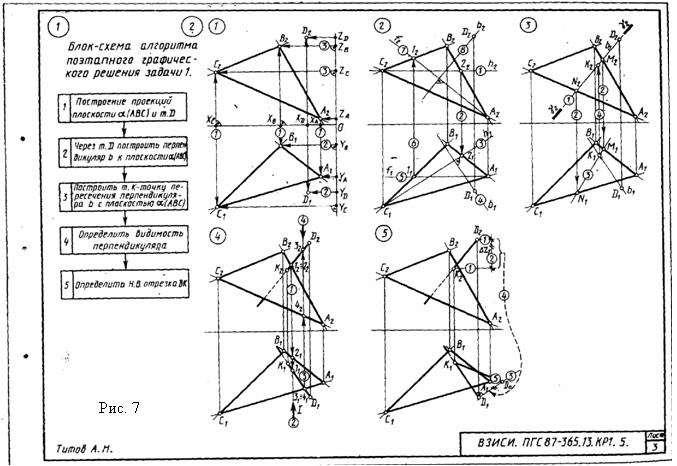
Задача 1. Построить блок-схему алгоритма поэтапного графического решения одной из трех задач листа 4 (см. условия задач к листу 4). Номер задачи для формализации в зависимости от варианта принимается по табл. 2, а исходные данные к ней - по табл., З.
Таблица 3
| Номер варианта | Значения координат, мм | ||||||||||||||
| ХА | YА | ZА | ХB | YB | ZB | ХC | YC | ZC | ХD | YD | ZD | ХE | YE | ZE | |
| б | 140. |
Указания к выполнению задачи 1. Представить решение задачи в виде определенной последовательности описаний элементарных графических задач; построение проекции плоскости а (А, В, С), построение к плоскости a(А, В, С) перпендикуляра, проходящего через т. D, и т. д. Каждая элементарная графическая задача оформляется блоком (прямоугольником с порядковым номером). Размеры блока 70х15 мм, расстояние между блоками 10 мм.
Задача 2. Осуществить поэтапное графическое выполнение задачи 1, 2 или 3 листа 4 в виде определенной последовательности решения элементарных графических задач с нанесением на изображение мнемонических знаков, раскрывающих порядок и характер выполнения элементарных графических процедур. Исходные данные те же, что и к задаче 1.
Указания к выполнению задачи 2. Каждую элементарную задачу оформляютотдельным эпюром в последовательности,указанной в блок-схеме. При построениипроекции тт. А, В, С, D, Е необходимочисловые значения их координат, принимаемые по табл., 3, уменьшить вдвое.
Мнемонические знаки принимают по табл. 4. Над каждой элементарной задачей размещают ее номер в кружке диаметром 7 мм (см. лист 3).
Лист 4
Формат АЗ. Основная надпись по форме 4 б. Выполнить три задачи на точку, прямую и плоскость в ортогональных проекциях, Пример выполнения листа см. на рис. 8. Задачи 1 и 2 совместить на одном чертеже в левой части листа, а задачу 3 расположить в правой части листа. Точку Е построить только для задачи З. Для левой в правой частей листа координатные оси показывать раздельно. В листе 4 и остальных листах контрольных работ обводку решенных задач выполнять цветной пастой шариковой ручки или тушью. Четко различать видимые и невидимые линии чертежа: видимые - сплошные толстые 0,6...0,8 мм; невидимые - штриховые 0,4 мм. Черной пастой обводят исходные данные, красной - полученный результат решения. Все промежуточные построения должны быть показаны на чертеже тонкими линиями 0,1...0,2 мм различными цветами (синим, зеленым, коричневым и т. д.) в зависимости от принадлежности к этапу решения задачи. Все вспомогательные построения не стирать и все точки чертежа обозначить.
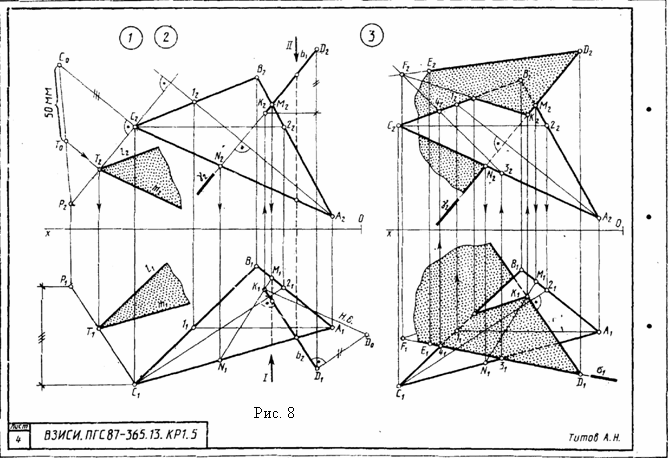
Задача 1. Дано: плоскость треугольника a(А, В, С) и точка D. Требуется определить расстояние от точки D до плоскости, заданной треугольником a(А, В, С). Определить видимость перпендикуляра, проходящего через точку D, и плоскости треугольникаa(А, В, С). Данные для выполнения задачи взять из та6л. 3, в соответствии с вариантом.
Указания к задаче 1. Задачу выполняют в такой последовательности: 1) из точки D опустить перпендикуляр, используя горизонталь h и фронталь f плоскости. При этом горизонтальная проекция перпендикуляра перпендикулярна горизонтальной проекции горизонтали h1, а фронтальная проекция перпендикуляра перпендикулярна фронтальной проекции фронтали f2; 2) определить точку пересечения перпендикуляра с плоскостью a(А, В, С), для чего перпендикуляр (прямую) заключают во вспомогательную, обычно проецирующую, плоскость (γ), находят линию пересечения плоскости a(А, В, С) и вспомогательной и отмечают точку К, в которой эта линия пересекается с перпендикуляром; 3) определяют натуральную величину (Н.В.) расстояния от точки D до плоскости a(А, В, С), применяя способ прямоугольного треугольника; 4) видимость проекции перпендикуляра определяют методом конкурирующих точек.
Таблица 4
| Содержание знаков | Изображение знаков |
| Порядок графической процедуры Параллельность Перпендикулярность Направление взгляда на П1 Направление взгляда на П2 Перенос | 
II
_|_
|
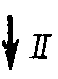
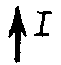
Задача 2. Дано: плоскость треугольника a(А, В, С). Требуется: построить плоскость, параллельную заданной и отстоящую от нее на 45...50 мм. Данные для выполнения задачи взять в табл. З.
Указания к задаче 2. Задачу выполняют в такой последовательности: 1) в заданной плоскости a(А, В, С) выбирают произвольную точку (в том числе вершину, на рис. 8 взята точка С) и из неё восстанавливают перпендикуляр к плоскости a(А, В, С), аналогично действию в первой задаче. В связи с тем, что задачи 1 и 2 совмещены на одном чертеже и направление перпендикуляра к плоскости a(А, В, С) уже выявлено - прямая b(D, К), то перпендикуляр через произвольно выбранную точку можно провести как прямую, параллельную перпендикуляру b(D, К). На эпюре одноименные проекции параллельных прямых параллельны; 2) определяют методом прямоугольного треугольника натуральную величину произвольного отрезка перпендикуляра, который ограничивают произвольной точкой Р; 3) на натуральной величине произвольного отрезка перпендикуляра находят точку Т, расположенную на заданном расстоянии 4...5 мм от плоскости, и строят проекции этой точки на проекциях перпендикуляра; 4) через точку Т строят искомую плоскость, соблюдая условие параллельности плоскостей: если плоскости параллельны, то две пересекающиеся прямые одной плоскости параллельны двум пересекающимся прямым другой плоскости. На эпюре одноименные проекции пересекающихся прямых параллельны.
Задача 3. Дано: плоскость треугольника a(А, В, С) и прямая а (D, Е). Требуется: через прямую а (D, Е) провести плоскость, перпендикулярную плоскости треугольника a (А, В, С), построить линию пересечения этих двух плоскостей, определить видимость. Данные для выполнения задачи взять из табл. 3.
Указания к выполнению задачи 3. Задача содержит следующие действия: 1) строят плоскость, перпендикулярную плоскости a (А, В, С). Плоскость, перпендикулярная другой плоскости, должна проходить через перпендикуляр к этой плоскости. Искомая плоскость, перпендикулярная плоскости a (А, В, С), должна содержать в себе заданную прямую а (D, Е) и перпендикуляр, опущенный из любой точки этой прямой на заданную плоскость a (А, С, В); (например, из точки В); 2) строят линию пересечения двух плоскостей: заданной плоскостью треугольника a (А, В, С) и построенной, перпендикулярной ей. Задачу на определение линии пересечения двух плоскостей можно решить двумя способами: первый - построить точки, пересечения двух прямых одной плоскости с другой плоскостью, т. е. использовать два раза схему нахождения точки пересечения прямой с плоскостью; второй - ввести две вспомогательные секущие плоскости частного положения, которые одновременно пересекали бы плоскость a (А, В, С) и плоскость, перпендикулярную ей, построить на линии пересечения с заданными плоскостями. Две собственные точки пересечения этих линий определяют линию пересечения данных плоскостей. В примере выполнения листа 4 (рис. 8) в задаче 3 применен первый способ. Точки пересечения прямой а (В, Е) и перпендикуляра b (D, К) определяют линию пересечения плоскостей a (А, В, С) и искомой перпендикулярной к ней; 3) определяют видимость пересекающихся заданных плоскостей. Видимость плоскостей устанавливают с помощью конкурирующих точек скрещивающихся прямых, принадлежащих этим плоскостям.
При решении задач 1, 2, 3 нужно помнить следующие положения ортогональных проекций,
1. Две проекции точки определяют ее положение в пространстве (относительно плоскостей проекций), так как по двум проекциям можно установить расстояние от точки до всех трех основных плоскостей проекций.
2. Ортогональные проекции одной и той же точки располагаются на перпендикуляре к оси проекции, который называется линией связи.
3. Если одна проекция прямой параллельна оси проекции, то такая прямая параллельна одной из плоскостей проекций, Принадлежащий ей отрезок проецируется на одну плоскость в натуральную величину (горизонтальная, фронтальная, профильная прямые). Если обе проекции прямой параллельны одной из осей проекций, то такая прямая занимает проецирующее положение, Одна из ее проекций вырождается в точку.
4. Проекция отрезка прямой общего положения всегда меньше отрезка в натуре.
5. Одноименные проекции параллельных прямых взаимно параллельны.
6. Точки пересечения одноименных проекций пересекающихся прямых расположены на одной и той же линии связи. Точки пересечения одноименных проекций скрещивающихся прямых не расположены на одной и той же линии связи.
7. Прямой угол проецируется на плоскость также в прямой угол, если одна его сторона параллельна этой плоскости.
8. Горизонталь, фронталь и линии наклона плоскости являются главными линиями плоскости. Фронтальная проекция горизонтали параллельна оси Х, горизонтальная проекция параллельна горизонтальному следу плоскости. Горизонтальная проекция фронтали параллельна оси Х, фронтальная проекция - фронтальному следу плоскости. Линии наклона плоскости перпендикулярны фронталям, горизонталям или профильным прямым плоскости. Угол их наклона к соответствующей плоскости проекций определяет угол наклона плоскости к той же плоскости проекций.
9. Линия пересечения любой плоскости с горизонтальной плоскостью является горизонталью, с фронтальной - фронталью.
Лист 5
Формат АЗ. Основная надпись по форме 4а. Выполнить две задачи на способы преобразования проекций. Пример выполнения листа представлен на рис. 9.
Задача 1. Дано: треугольник АВС. Требуется: способом вращения вокруг осей, перпендикулярных плоскостям проекций, определить величину треугольника АВС. данные для выполнения задачи берут из табл. 5.
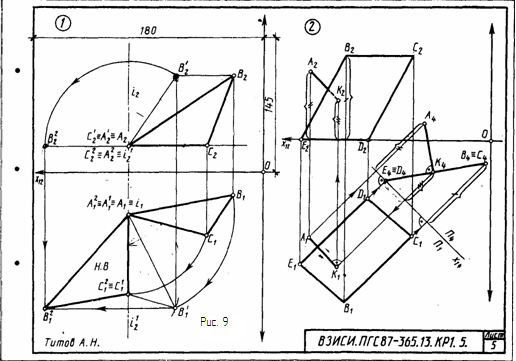
Указания к задаче 1. Соблюдая правила вращения геометрических фигур вокруг оси, перпендикулярной плоскости проекций, необходимо выполнить два действия: 1) привести треугольник АВС в положение проецирующей плоскости, т. е. перпендикулярной плоскости проекций. Признаком перпендикулярности заданной плоскости плоскостям проекций на эпюре является вырождение одной из проекций плоскости треугольника a (А, В, С) в прямую линию, для получения фронтально-проецирующей плоскости необходимо горизонталь плоскости a (А, В, С) вместе с системой всех точек треугольника АВС поставить в положение, перпендикулярное фронтальной плоскости проекций, а для получения горизонтально-проецирующей плоскости необходимо фронталь плоскости a (А, В, С) со всеми точками плоскости перевести в положение прямой, перпендикулярной горизонтальной плоскости проекций;
2) полученную проецирующую плоскость преобразовать в плоскость уровня, т. е. параллельную либо горизонтальной, либо фронтальной плоскости проекций, в зависимости от ее положения на первом этапе преобразования. Для этого выродившуюся в прямую линию проекцию треугольника АВС изобразить в положении, параллельном оси Х. Проекция треугольника АВС на одной из плоскостей проекций и будет являться натуральной величиной треугольника АВС.
При вращении фигур вокруг осей, перпендикулярных плоскостям проекций, необходимо учитывать следующее:
1. Линия перемещения точки (траектория) представляет собой окружность. Так как плоскость траектории параллельна плоскости проекций, то проекции точки перемещаются: одна - по окружности, другая по прямой, параллельной оси проекций,
2. Проекция фигуры на ту плоскость проекций, на которой ось вращения проецируется в точку, не изменяется ни по величине, ни по форме, изменяется только е положение относительно оси проекций.
З. Ось проекций не участвует в решении задач (как это имеет место при замене плоскостей проекций), поэтому на чертеж она может быть не проведена.
Таблица 5
| № варианта | Значения координат, мм | ||||||||
| ХА | YА | ZА | ХB | YB | ZB | ХC | YC | ZC | |
Задача 2. Дано: четырехугольник ЕВСD и точка А. Требуется: способом замены плоскостей проекций определит расстояние от точки А до плоскости a (Е, В, С, D), построить проекции этого расстояния на исходном эпюре и описать последовательность выполнений графических процедур решения задачи способом, показанным на листе З (см. рис. 7). Точки Е, В, С, D для всех вариантов имеют одинаковые координаты: Е(90, 60, 10), В(60, 90, 80), С(10, 60, 80), D(40, 30, 10).
Координаты точки А берут из табл. 6.
Таблица 6
| Варианты | ||||||||||
| Координаты точек | Значение координат, мм | |||||||||
| XA YA ZA |
Указания к задаче 2. Соблюдая правила построения геометрических фигур на знаменных плоскостях проекций, необходимо 1) преобразовать плоскость общего положения a (Е, В, С, D) в плоскость фронтально-проецирующую и построить проекцию точки А. Положение новой плоскости определяет новая ось проекций Х14, Она должна располагаться перпендикулярно горизонтальной проекции горизонтали плоскости a (Е, В, С, D), 2) определить расстояние от точки А до заданной плоскости. Оно равно отрезку перпендикуляра АК, опущенного из точки А на плоскость a (Е, В, С, D), выродившуюся на новой фронтальной плоскости проекций в прямую линию; 3) получив основание перпендикуляра (К4), построить его проекции на исходном чертеже задачи. Так как проекция отрезка А4К4 перпендикуляра b - натуральная величина отрезка, то, следовательно, его проекция на плоскость П1 будет параллельна оси Х14. Координату Z для плоскости П2 следует снять с плоскости проекций П4; 4) описание последовательности графических процедур при решении задачи выполнять по аналогии с примером, приведенным на рис. 7.
При изучении способа замены плоскостей нужно иметь в виду, что фигура не меняет своего положения в пространстве, плоскость же проекций П1 или П2 заменяют плоскостью, соответственно П5 или П4. Такую замену проводят последовательно, сначала заменяют одну плоскость, затем другую.
При построения проекции фигуры на новой плоскости проекций необходимо помнить, что происходит переход от одного эпюра к другому, на котором соответственные проекции точек также расположены на линиях связи. Координата точки на но плоскости проекций равна координате точки на заменяемой плоскости проекций.
Лист 6
Формат АЗ. Основная надпись по форме 4б. Выполнить две задачи на пересечение многогранных поверхностей и определение натуральной величины сечения многогранника плоскостью. Пример выполнения листа на рис. 10.
Задача 1. Дано: прямая четырехгранная пирамида и трехгранная горизонтальная призма. Требуется: вычертить три проекции пирамиды и призмы, построить линию пересечения этих многогранников и определить ее видимость, для всех вариантов стороны основания пирамиды Р1F1 = К1Е1 = 60 мм; К1Р1=Е1F1=70 мм; высота пирамиды 110 мм; высота вертикальной грани призмы 90 мм; длина всех ребер призмы 140 мм (рис. 10). Величины l, h, <a, а также значения координат точек Р и D берут из табл. 7 в соответствии с номером варианта.
Таблица 7
| № варианта | XP | YP | ZP | XD | YD | ZD | l | h | Угол a | Секущая грань |
| А СN М B DN М А СN М B DN М B DN М А СN М B DN М А СN М B DN М АСNМ |
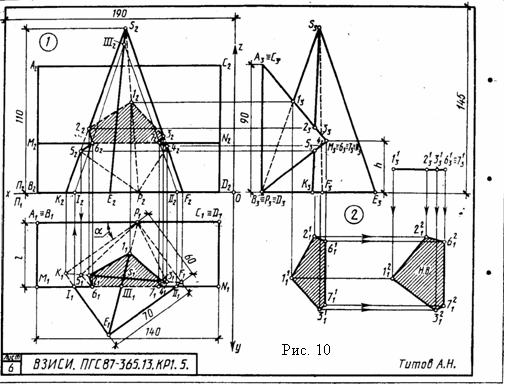
Указания к задаче 1. Вычерчивание пирамиды нужно начинать с точки Р, а призмы - с точки D. Основание пирамиды расположено в плоскости П1, ее ребра прямые общего положения. Одна из граней призмы - фронтальная плоскость (параллельная П2). Две других - профильнопроецирующие, поэтому ребра этих граней на плоскости П3 проецируются в точки.
Линия пересечения многогранников определяется по точкам пересечения ребер каждого из них с гранями другого многогранника или построением линий пересечения граней многогранников. Соединяя каждые пары точек одних и тех же граней отрезками прямых, получаем линии пересечения многогранников. Видимыми линиями пересечения многогранников будут те, которые принадлежат их видимым граням. Линия пересечения многогранников строится только с использованием фронтальных и горизонтальных проекций фигур. Профильные проекции фигур применить для проверки правильности определения точек пересечения ребер с гранями и их последовательного соединения.
Задача 2. Дано: прямая четырехгранная пирамида и одна грань призмы. Требуется: способом плоскопараллельного перемещения определить натуральную величину сечения пирамиды с гранью призмы. Исходные данные берут из табл. 7.
Указания к задаче 2. Для выполнения данной задачи используют результат решения задачи 1, выделяя из него часть линии пересечения, которая относится к указанной для варианта грани по табл. 7. Профильную проекцию пирамиды с заданной секущей гранью призмы принимают за фронтальную проекцию и к ней достраивают горизонтальную проекцию сечения пирамиды гранью по уже имеющейся горизонтальной проекции в задаче 1, но соответственно развернув его в проекционной связи (см. рис. 10). Так как секущая грань занимает положение проецирующей плоскости то, чтобы получить натуральную величину сечения, достаточно произвести одно перемещение. Способом плоскопараллельного перемещения проецирующую плоскость грани ставим в положение плоскости уровня (параллельное горизонтальной плоскости проекций).
При способе плоскопараллельного перемещения все точки фигуры перемещаются в плоскостях, параллельных какой-либо одной плоскости проекций. Поэтому проекция траекторий точек на вторую плоскость проекций представляют собой прямые линии, параллельные оси проекций. Как и про вращении вокруг осей, перпендикулярных плоскостям проекций, при плоскопараллельном перемещении одна проекция фигуры не меняется ни по величине, ни по форме.
КОНТРОЛЬНАЯ РАБОТА 2
(Листы 7...12. Листы 8, 10, 12 соответственно выполняются на обороте листов 5, 7, 9, 11)
Лист 7
Формат АЗ. Основная надпись по форме 4а. Выполнить три задачи на пересечение поверхности плоскостью и прямой. Пример выполнения листа на рис. 11. Задачи 1 и 2 выполняют в левой части листа, одна под другой, а задачу 3 в правой части листа.
Задача 1. Дано: пирамида и прямая l. Требуется: определить точки пересечения прямой l с поверхностью трехгранной пирамиды. Все варианты задач имеют два одинаковых параметра: высоту пирамиды 70 мм и диаметр вспомогательной окружности 60 мм, в которую вписывается треугольное основание произвольного расположения (по усмотрению студента). Положение прямой общего положения, которая пересекает пирамиду, также устанавливается студентом самостоятельно.
Указания к задаче 1. Чтобы решить задачу, необходимо: 1) заключить прямую во вспомогательную плоскость частного положения (фронтально - проецирующую или горизонтально - проецирующую); 2) построить линию пересечения пирамиды с этой вспомогательной плоскостью; 3) отметить точки пересечения проекций прямой с проекциями линии пересечения: 4) определить видимость
Так как плоскость, в которую заключается прямая, частного положения, то одна из проекций фигуры сечения пирамиды совпадает с проекцией секущей плоскости, выродившейся в линию. Вторую проекцию сечения достраивают по точкам фигуры сечения, которые лежат непосредственно на ребрах. Задача может иметь одно из трех решений: прямая пересекает пирамиду в двух точках, в одной точке (касается) и не пересекает поверхность.
Задача 2. Дано: основание конуса - окружность диаметра 60 мм, высота конуса 70 мм и прямая l. Требуется: определить точки пересечения прямой l с поверхностью прямого кругового конуса. Положение прямой студент выбирает самостоятельно, учитывая характеристику прямой, указанную в табл. 8.
Указания к задаче 2. Чтобы решить задачу, необходимо выполнить действия, аналогичные перечисленным в указаниях к задаче 1. При этом следует напомнить, что выбирать нужно такие вспомогательные секущие плоскости, которые дают наипростейший контур сечения конуса: окружность и треугольник. Так, например, для задачи 2, помещенной на рис. 11, вспомогательная секущая плоскость является плоскостью общего положения, которая проходит через вершину конуса и задана двумя пересекающимися прямыми (заданной прямой и произвольной прямой, проходящей через вершину конуса и точку К данной прямой). Такая плоскость дает сечение в виде треугольника. Если через горизонтальную прямую провести горизонтальную плоскость, сечение будет иметь форму окружности. После определения точек пересечения прямой с конусом не забудьте установить видимые отрезки прямой.
Таблица 8
| № варианта | Характеристика прямой l |
| Нисходящая общего положения Фронтальная под углом к П1 45° Горизонтально-проецирующая Горизонтальная под углом к II2 30° Фронтально-проецирующая Восходящая общего положения Горизонтальная под углом к П2 45° Фронтально-проецирующая Фронтальная под углом к П1 30° Горизонтально-проецирующая |
Задача 3. Построить три проекции линии пересечения сложной поверхности с фронтально - проецирующей плоскостью и способом совмещения (вращения вокруг линии уровня) определить натуральную величину этого сечения. Данные для вычерчивания комбинированной поверхности берут и табл. 9. Таблица 9
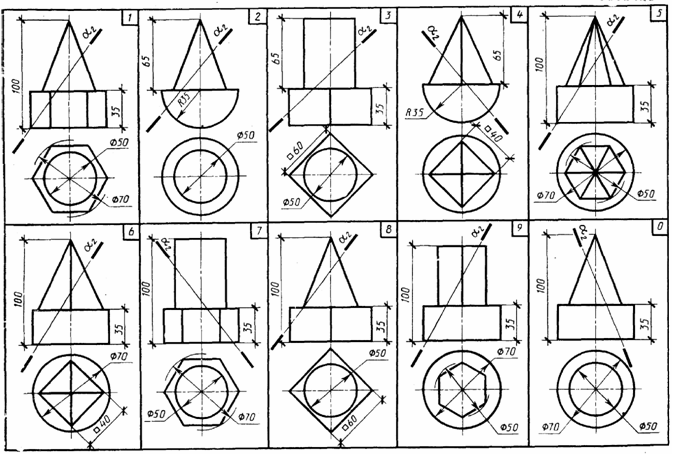
Указания к задаче 3. Задачу размещают на правой стороне листа (см. рис. 11). Высота всей комбинированной поверхности равна 100 мм, нижняя ее часть - 35 мм. Размеры диаметров оснований поверхностей и вспомогательных окружностей, а также стороны многоугольников приведены в табл. 9. Положение секущей плоскости для своего варианта студент назначает самостоятельно. Задачу решают в два этапа: 1) строят проекции сечения; 2) определяю натуральную величин сечения указанным способом.
Так как в данном задании для пересечения предложена плоскость частного положения фронтально - проецирующая, то решение задачи сводится к построению проекций ряда точек фигуры сечения заданной поверхности как точек, расположенных на образующих или направляющих линиях этой поверхности. Первоначально крайние и промежуточные точки сечения назначаются на следу секущей плоскости. Натуральную величину сечения определяют по тем же точкам, которые были установлены на первом этапе. За ось вращения плоскости сечения выбирают фронталь плоскости сечения, совпадающую с его осью симметрии. Для того чтобы избежать наложения изображений, фронталь следует размещать на свободном поле чертежа параллельно следу секущей плоскости. Каждая точка сечения будет вращаться вокруг оси в плоскости, перпендикулярной ей. Радиус вращения отображен в натуральную величину на горизонтальной плоскости проекций и соответствует расстоянию от точки до продольной оси симметрии (оси вращения).
Лист 8
Формат АЗ. Основная надпись по форме 4 б. Выполнить две задачи на пересечение многогранных и кривых поверхностей и построение разверток поверхностей. Пример выполнения листа на рис. 12.
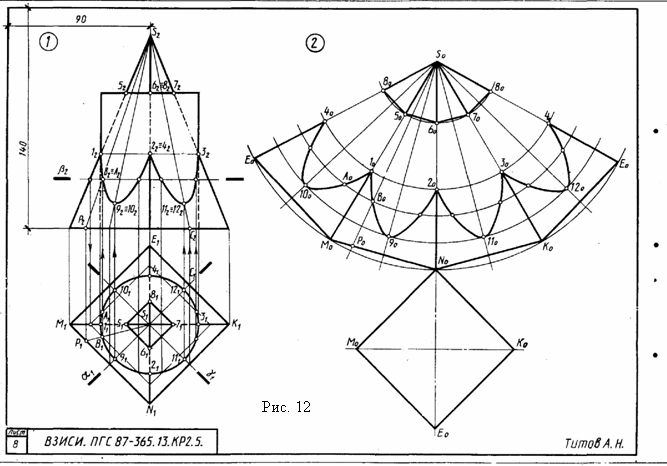
Задача 1. Дано: многогранник и кривая поверхность. Требуется: способом вспомогательных секущих плоскостей построить линию пересечения многогранной и кривой поверхностей, выделив ее видимые и не видимые участки. Данные для задачи берут из табл. 10.
Указания к задаче 1. Задачу выполняют на левой половине листа в такой последовательности: 1) намечают расположение вспомогательных секущих плоскостей частного положения (уровня) или проецирующих; 2) с их помощью определяют характерные и промежуточные точки линии пересечения поверхностей; 3) полученные точки соединяют плавными кривыми или прямыми линиями, установив предварительно последовательность расположения точек на линии пересечения поверхностей. Видимую часть линий контура, в том числе и линии пересечения, обводят сплошной основной, а невидимую - штриховой линиями. При решении задач на взаимное пересечение поверхностей следует помнить следующие положения.
1. Чтобы построить точку, принадлежащую линии пересечения поверхностей, нужно обе поверхности рассечь вспомогательной плоскостью (иногда вспомогательной поверхностью) и, найдя линии пересечения вспомогательной плоскости с заданными поверхностями, отметить общие для них точки. Плоскость следует выбирать так, чтобы линии ее пересечения с поверхностями проецировались в простейшие фигуры (окружности или прямые). Использование нескольких вспомогательных плоскостей позволяет определить ряд точек линий пересечения. Соединять можно только те точки, которые расположены в одной грани многогранника.
2. Когда боковая поверхность цилиндра или призмы занимает относительно плоскости проекций проецирующее положение (образующие поверхности перпендикулярны этой плоскости проекций), то одна проекция линии пересечения поверхностей становится известной без дополнительных построений - она совпадает с проекцией поверхности.
З. Если линия, принадлежащая поверхности, видна не полностью, то точки перехода от видимой части линии пересечения к невидимой располагаются на очерке поверхности. Видимая часть линии пересечении поверхностей должна быть видимой как на одной поверхности, отдельно взятой, так и на другой.
4. Чтобы найти верхнюю или нижнюю точку линии пересечения, соответствующей грани с конусом, нужно взять такую вспомогательную плоскость, которая должна проходить через вершину конуса перпендикулярно этой грани призмы. (Для прямой призмы перпендикулярно ребрам основания)
Задача 2. Дано: две пересекающиеся поверхности - многогранник и кривая поверхность и линия их пересечения. Требуется: построить полную развертку одной из пересекающихся поверхностей и нанести на ней линию их пересечения. Поверхность для построения развертки студент выбирает сам из двух поверхностей задачи 1 в соответствии со своим вариантом.
Таблица 10
Линия пересечения поверхностей наносится по результату решения задачи 1.
Указания к задаче 2. Задачу выполняют на правой половине листа в такой последовательности; 1) в кривую поверхность вписывают многогранник; 2) определяют натуральные величины всех ребер вписанного многогранника; 3) на плоскости чертежа строят одну из граней поверхности по натуральным величинам ребер и к ней последовательно пристраивают остальные грани, пользуясь смежными ребрами; 4) соответствующие вершины граней соединяют плавными кривыми линиями.
При развертывании многогранной поверхности выполняют только вторую и третью операции. Линия пересечения поверхностей наносится на развертку с помощью ее характерных точек. Для каждой такой точки в ортогональных проекциях определяют положение образующей и направляющей линий поверхности, на пересечении которых расположена взятая точка. Строят эти линии (образующую и направляющую) на развертке и в их пересечении отмечают искомую точку линии пересечения поверхностей (рис. 12).
Лист 9
Формат АЗ. Основная надпись по форме 4 а. Выполнить две задачи на построение линии пересечения п
верхностей различными способами. Пример выполнения листа представлен на рис. 13.
о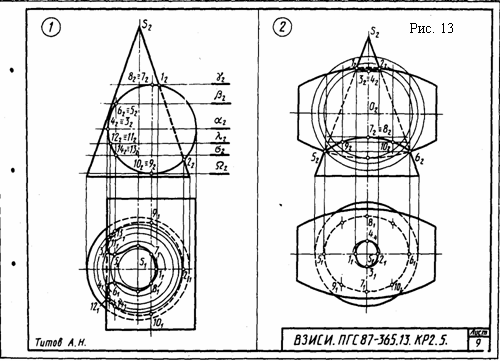 
Задача 1. Дано: две пересекающиеся кривые поверхности. Требуется: способом вспомогательных секущих плоскостей построить линию их пересечения, выделив видимые и невидимые участки. Данные варианта задачи берут из табл. 11. Таблица 11
Указания к задаче 1. Задачу выполняют с левой стороны листа в такой последовательности: 1) определяют точки пересечения очерковых образующих одной поверхности с другой, а затем второй поверхности с первой; 2) определяют наивысшие и наинизшие точки линии; 3) определяют промежуточные точки линии пересечения; 4) все найденные точки пересечения последовательно соединяют кривой линией, учитывая видимость.
При выборе вспомогательных секущих плоскостей необходимо помнить, что они должны пересечь одновременно обе поверхности и дать наипростейшие фигуры сечения. Для всех вариантов заданий вспомогательно - секущими плоскостями могут быть выбраны плоскости уровня; для одних - горизонтальные, для других - вертикальные или те и другие. Точками пересечения поверхностей являются точки пересечения контуров фигур сечения поверхностей, лежащих в одной и той же вспомогательно - секущей плоскости. Каждая секущая плоскость может определить от одной до четырех точек линии пересечения в зависимости от характера пересекающихся поверхностей, их расположения относительно друг друга и положения самой секущей плоскости.
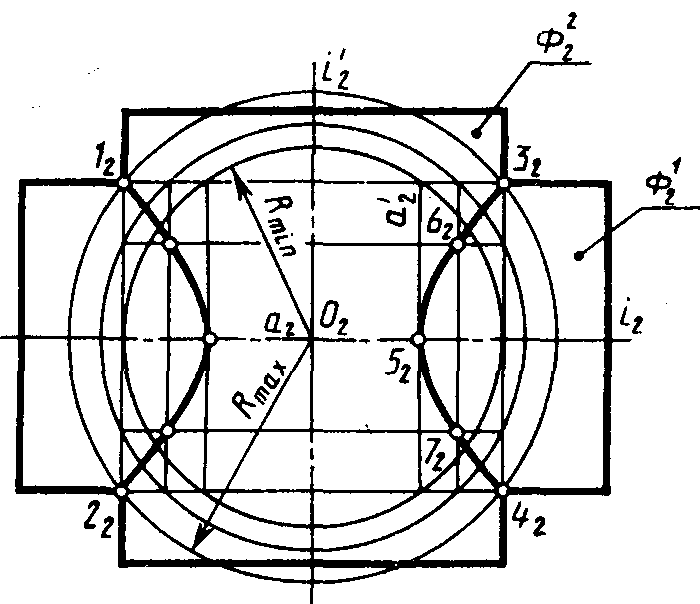
Задача 2. Дано: две пересекающиеся поверхности вращении. Требуется: способом секущих концентрических сфер построить линию их пересечения и определить ее видимость. Данные варианта задачи берут из табл. 12. Таблица 12
| Рис. 15 |
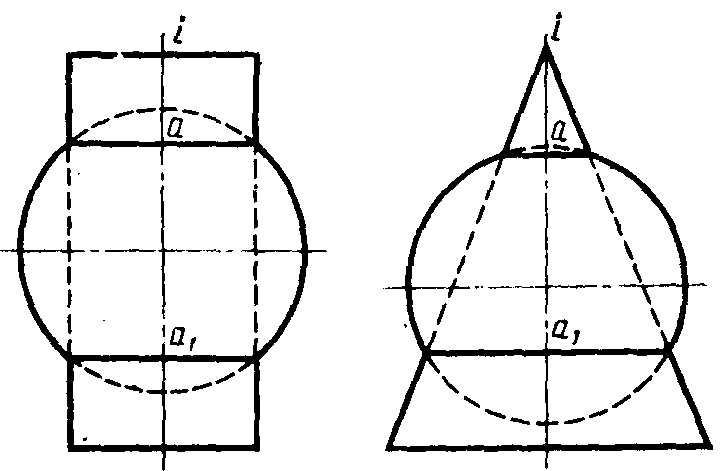
| Рис. 14 |
Поиск по сайту: