Численное дифференцирование

К численному дифференцированию приходится прибегать в том случае, когда функция f (x), для которой нужно найти производную, задана таблично, или же функциональная зависимость x и f (x) имеет сложное аналитическое выражение. В первом случае методы дифференциального исчисления просто неприменимы, а во втором случае их использование вызывает значительные трудности.

Во всех этих случаях вместо функции f (x) рассматривают интерполирующую функцию j(х) и считают производную от f (x) приближенно равной производной от j(х). Естественно, что производная от f (x) будет найдена с некоторой погрешностью.

Существуют два основных источника возможного появления значительных погрешностей при численном дифференцировании. Функцию f(x) можно записать в виде

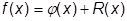, (28.1)

где j(х) – интерполирующая функция, а R (x) – остаточный член интерполяционной формулы. Предполагая, что f (x) и j(х) имеют производные k -того порядка, можно найти эти производные, дифференцируя тождество (5.1) k раз:

. (28.2)

Так как за приближенное значение принимается величина , то величина погрешности численного дифференцирования будет равна .

При замене f (x) интерполирующей функцией j(х) предполагается, что остаточный член (то есть величина R (x)) мал, но из этого совсем не следует, что мало . Производные от малой функции могут быть весьма большими. Особенно это относится к производным высших порядков. Данная ситуация иллюстрируется на рис.28.1.

Даже в случае, когда интерполяционный многочлен хорошо аппроксимирует табличную функцию, его производные могут ничего не иметь общего с производными аппроксимируемой функции.

Вторая причина обусловлена использованием табличных данных, полученных экспериментальным путем. Эти значения всегда содержат некоторую погрешность, так называемый шум. Если продифференцировать эти значения, то наличие экспериментальных погрешностей значительно увеличит погрешность определения производной истинной функции.

Поиск по сайту: