Векторная форма

89. В дифференциальной форме закон Фарадея можно записать в следующем виде:

(в системе СИ)

90. или

(в системе СГС).

91. В интегральной форме (эквивалентной):

(СИ)

92. или

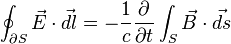(СГС)

93. Здесь — напряжённость электрического поля, — магнитная индукция, — произвольная поверхность, — её граница. Контур интегрирования подразумевается фиксированным (неподвижным).

94. Следует отметить, что закон Фарадея в такой форме, очевидно, описывает лишь ту часть ЭДС, что возникает при изменении магнитного потока через контур за счёт изменения со временем самого поля без изменения (движения) границ контура (об учете последнего см. ниже).

В этом виде закон Фарадея входит в систему уравнений Максвелла для электромагнитного поля (в дифференциальной или интегральной форме соответственно)^[2].

95. Если же, скажем, магнитное поле постоянно, а магнитный поток изменяется вследствие движения границ контура (например, при увеличении его площади), то возникающая ЭДС порождается силами, удерживающими заряды на контуре (в проводнике) и силой Лоренца, порождаемой прямым действием магнитного поля на движущиеся (с контуром) заряды. При этом равенство продолжает соблюдаться, но ЭДС в левой части теперь не сводится к (которое в данном частном примере вообще равно нулю). В общем случае (когда и магнитное поле меняется со временем, и контур движется или меняет форму) последняя формула верна так же, но ЭДС в левой части в таком случае есть сумма обоих слагаемых, упомянутых выше (то есть порождается частично вихревым электрическим полем, а частично силой Лоренца и силой реакции движущегося проводника).

Некоторые авторы, например, М. Лившиц в журнале «Квант» за 1998 год^[3] отрицают корректность применения термина закон Фарадея или закон электромагнитной индукции и т. п. к формуле в случае подвижного контура (оставляя для обозначения этого случая или его объединения со случаем изменения магнитного поля, например, термин правило потока)^[4]. В таком понимании закон Фарадея — это закон, касающийся лишь циркуляции электрического поля (но не ЭДС, создаваемой с участием силы Лоренца), и в этом понимании понятие закон Фарадея в точности совпадает с содержанием соответствующего уравнения Максвелла.

Однако возможность (пусть с некоторыми оговорками, уточняющими область применимости) совпадающей формулировки «правила потока» с законом электромагнитной индукции нельзя назвать чисто случайной. Дело в том, что, по крайней мере для определенных ситуаций, это совпадение оказывается очевидным проявлением принципа относительности. А именно, например, для случая относительного движения катушки с присоединенным к ней вольтметром, измеряющим ЭДС, и источника магнитного поля (постоянного магнита или другой катушки с током), в системе отсчета, связанной с первой катушкой, ЭДС оказывается равной именно циркуляции электрического поля, тогда как в системе отсчета, связанной с источником магнитного поля (магнитом), происхождение ЭДС связано с действием силы Лоренца на движущиеся с первой катушкой носители заряда. Однако та и другая ЭДС обязаны совпадать, поскольку вольтметр показывает одну и ту же величину, независимо от того, для какой системы отсчета мы её рассчитали.

Если проводник перемещается в постоянном магнитном поле, то в нём также появляется ЭДС

индукции. Однако причиной теперь служит не вихревое электрическое поле (оно не возникает

— ведь магнитное поле постоянно), а действие силы Лоренца на свободные заряды проводника.

Рассмотрим ситуацию, которая часто встречается в задачах. В горизонтальной плоскости

расположены параллельные рельсы, расстояние между которыми равно l. Рельсы находятся в

8вертикальном однородном магнитном поле B~. По рельсам движется тонкий проводящий стер-

жень P N со скоростью ~v; он всё время остаётся перпендикулярным рельсам

Возьмём внутри стержня положительный свободный заряд q. Вследствие движения этого заряда вместе со стержнем со скоростью ~v на заряд будет действовать сила Лоренца: F = qvB. Направлена эта сила вдоль оси стержня, как показано на рисунке (убедитесь в этом сами — не забывайте правило часовой стрелки или левой руки!). Сила Лоренца F~ играет в данном случае роль сторонней силы: она приводит в движение свободные заряды стержня. При перемещении заряда q от точки N к точке P наша сторонняя сила совершит работу: A = Fl = qvBl. (Длину стержня мы также считаем равной l.) Стало быть, ЭДС индукции в стержне окажется равной: Ei = A q = vBl

Поиск по сайту: