АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Статические моменты

Читайте также:
  1. Выборочные моменты
  2. Гетеростатические теории личности: ориентация на согласие
  3. Многообразие типов и видов деятельности. Опредмечивание и распредмечивание как моменты деятельности.
  4. Моменты инерции некоторых однородных тел
  5. Моменты оперативного приема
  6. Моменты распределения.
  7. Моменты случайной величины
  8. Область видимости. Локальные переменные. Глобальные переменные. Статические локальные переменные.
  9. Осевые моменты инерции некоторых тел
  10. Основные требования ИР. Статические и динамические потери
  11. Положительные моменты привлечения краткосрочных кредитов
  12. Понятие производства: его сущность и предпосылки. Простые моменты процесса труда

Если m = 1, n = 0, тогда получим характеристику

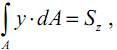
которая называется статическим моментом относительно оси z, или, при

m = 0, n = 1,

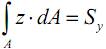
статическим моментом относительно оси y.

Статический момент относительно данной оси – сумма произведений элементарных площадей dA на их расстояние до данной оси, взятая по всей площади сечения А.

На основании теоремы Вариньяна (из курса теоретической механики) следует, что

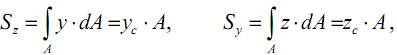
а для сложного сечения (состоящего из нескольких простых, каждое из которых имеет площадь Ai и координаты собственного центра тяжести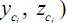

Статический момент относительно какой-либо оси равен произведению всей площади фигуры на расстояние от ее центра тяжести до этой оси.

Отсюда можем получить формулы для определения координат центра тяжести сечения:

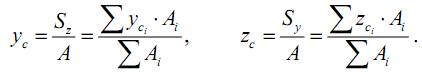
Как видим, относительно осей, проходящих через центр тяжести сечения, статические моменты равны нулю, а сами эти оси называются центральными. Размерность статических моментов – м3 в системе СИ.

 


1 | 2 | 3 | 4 | 5 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.002 сек.)