ЭЛЕМЕНТЫ МЕХАНИКИ ЖИДКОСТЕЙ И ГАЗОВ

1. Определение усилий, действующих на тела, движущиеся в жидкости или газе, например определение силы лобового сопротивления самолёта для расчета мощности его двигателя, определение силы торможения парашюта, расчёт ветровой нагрузки телебашен, линий электропередач и т.д.

2. Определение наиболее выгодных форм тел, например формы крыльев самолёта, корпуса подводной лодки, лопаток турбины и т.п.

3. Определение режима течения в каналах, трубах. Если, например, ламинарный режим изменяется на турбулентный, то изменяются и уравнения, описывающие течения, и конечные решения.

4. Изучение распространения механических волн, например распространения ультразвуковых волн при локации кораблей и подводных лодок, изучение закономерностей ударных волн, возникающих при взрыве атомных бомб, от самолётов, движущихся со скоростями больше скорости звука в атмосфере.

2. Понятие о сжимаемости и вязкости. Пусть имеется деформируемое тело длиной L, которое мы в некоторый момент начнём толкать слева направо со скоростью (рис. 5.1). Придёт ли всё тело сразу в движение со скоростью ? Нет. Левый конец начнёт двигаться сразу. По телу от левого конца к правому побежит волна упругого воздействия со скоростью звука . В течение времени правый конец не будет «знать», что левый конец двигается, и будет стоять. За это время левый конец пройдёт расстояние . Тело станет короче на величину , т.е. сожмётся на эту величину. Относительное сжатие тела будет:

.

Отношение обозначают числом и называют числом Маха по имени австрийского физика и философа Эрнста Маха (1838 – 1916). Видно, что сжимаемость равна отношению скорости движения к местной скорости звука – числу Маха. Чем больше скорость звука в веществе, тем меньше его сжимаемость. Скорость звука в воздухе примерно равна 330, в воде – 1400 и в металлах – 4000 – 7000 м/c.

Условно считают, что если , то жидкость несжимаемая, а если , то жидкость сжимаемая. Например, если пуля летит со скоростью примерно 800 м/с в воде, то . Поэтому вода для летящей пули – сжимаемая жидкость.

Вязкость. Все реальные жидкости являются вязкими. Вязкость (внутреннее трение) проявляется в том, что при движении в жидкости тело встречает сопротивление. Из опыта известно: чтобы поддерживать постоянным течение жидкости в трубе, необходимо наличие между концами трубы разности давлений. Необходимость сил давления указывает на то, что эти силы уравновешиваются какими-то силами, тормозящими движение. Этими силами являются силы внутреннего трения на границе со стенкой трубы и на границах между слоями. Более быстрый слой стремится увлечь за собой более медленный слой, действуя на него с силой , направленной по течению. Одновременно более медленный слой стремится замедлить движение более быстрого слоя, действуя на него силой , направленной против течения (рис. 5.2). Экспериментально установлено, что модуль силы внутреннего трения, приложенной к площадке S, лежащей на границе между слоями, определяется формулой:

где коэффициент пропорциональности, зависящий от природы жидкости и её состояния (например температуры); производная скорости жидкости по радиусу, показывающая, как быстро изменяется в данном месте скорость течения в направлении оси r, перпендикулярной к площадке S.

Под идеальной жидкостью понимают жидкость, в которой нет сил внутреннего трения, т.е. вязкость равна нулю (более строго говорят, что жидкость не оказывает сопротивления деформации сдвига).

Поле скоростей. Движение жидкости характеризуется совокупностью функций скоростей, с которыми проходят через каждую точку отдельные частицы жидкости. Совокупность векторов , заданных для всех точек пространства течения жидкости, называется полем вектора скорости. Это поле наглядно можно изобразить с помощью линий тока. Линия тока – такая линия, в каждой точке которой в данный момент времени вектор скорости направлен по касательной.

Поверхность тока – совокупность линий тока, проходящих через некоторую кривую (рис. 5.3). Часть жидкости, ограниченная замкнутой поверхностью тока, называется трубкой тока. Если скорость в каждой точке пространства остаётся постоянной (), то течение жидкости называется стационарным (установившимся).

3. Уравнение неразрывности. Пусть имеется достаточно тонкая трубка тока (скорость во всех точках поперечного сечения одинакова) несжимаемой жидкости. При стационарном течении трубка тока подобна стенкам жёсткой трубы. Поэтому через сечение S за время пройдёт объём жидкости 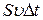, а в единицу времени .

Возьмём 2 сечения трубки тока (рис. 5.4). Если жидкость несжимаемая, то количество её между этими сечениями остаётся неизменным. Отсюда следует, что объёмы жидкости, протекающие в единицу времени через сечения и , должны быть одинаковыми: . Это равенство справедливо для любой пары произвольно взятых сечений. Следовательно, для несжимаемой жидкости при стационарном течении произведение в любом сечении данной трубки тока имеет постоянное значение:

Это утверждение носит название теоремы о неразрывности струи. Она применима даже к газам, если их сжимаемостью можно пренебречь (). Примеры: 1) в узком месте река течёт быстро, в широком – медленно; 2) пожарный брандспойт имеет сужающийся наконечник, чтобы скорость воды была больше и струя летела дальше.

Поиск по сайту: