|
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Об’ємів тіл обертання
План.
1. Площі плоских фігур. 2.Об’єми тіл обертання.
1. Площі плоских фігур.
На практиці доводиться обчислювати площі фігур, які не є криволінійними трапеціями. Щоб обчислити площу фігури, обмежену кількома лініями, то знаходять криволінійні трапеції, переріз або об’єднання яких є дана фігура, обчислюють площі кожної з них і знаходять суму або різницю площ цих криволінійних трапецій.
Площа криволінійної трапеції
  y y=f(x) y y=f(x)
          a b х
a b х
| |||
    Обчислення площ Обчислення площ
 y=f(x) y=f(x)
   y=g(x) y=g(x) 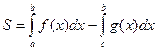 a c b x
a c b x
| |||
a b
y=f(x)
| |||
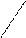     y=f(x) y=g(x) y=f(x) y=g(x)
     
 a b c x a b c x
| |||
     y=f(x)
a b x y=f(x)
a b x       
 y=g(x) y=g(x)
|
2.Об’єми тіл обертання.
Поняття інтеграла може бути використане для виведення формули об’ємів тіл.
Розглянемо практичний приклад. Нехай нам треба знайти об’єм лимона, що має неправильну форму, і тому використати відомі формули для знаходження об’ємів неможливо. Поступим так. Розріжем лимон на тоненькі дольки. Кожну дольку приблизно можна вважати циліндром, радіус якого можна виміряти. Об’єм циліндра можна знайти за відомою формулою. Склавши об’єми маленьких циліндрів, ми одержимо приблизно об’єм всього лимона. Наближення буде тим точніше, чим тонкіше розрізати лимон.

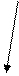 S(x)
S(x)

 z
z
 | |||
 | |||

 0 a x b
0 a x b


 x y
x y
Використаємо аналогічну процедуру для обчислення об’ємів тіл обертання.
Нехай тіло, об’єм якого треба обчислити, розміщене між двома паралельними площинами. Введем систему координат так, щоб вісь абсцис була перпендикулярна цим площинам. Позначимо S(x) – площу перерізу тіла площиною, перпендикулярною осі абсцис і яка перетинає її в точці х, функція S(x) неперервна на відрізку  .
.
Розділимо відрізок  на n рівних відрізків: х0=а, х1, х2, …. хn-1, xn=b і через ці точки проведемо площини, перпендикулярні осі ОХ. Площини розріжуть дане тіло на n шарів. Об’єм даного тіла дорівнює сумі об’ємів шарів з основами S(x0), S(x1), S(x2), …S(xn-1) і висотою
на n рівних відрізків: х0=а, х1, х2, …. хn-1, xn=b і через ці точки проведемо площини, перпендикулярні осі ОХ. Площини розріжуть дане тіло на n шарів. Об’єм даного тіла дорівнює сумі об’ємів шарів з основами S(x0), S(x1), S(x2), …S(xn-1) і висотою  .
.

Точність цього наближення тим вища, чим більше n, тт. тонкі прошарки. Природно вважати, що об’єм даного тіла дорівнює границі об’єму Vn, n 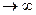 , V=
, V=  .Сума Vn є інтегральною сумою для неперервної на відрізку
.Сума Vn є інтегральною сумою для неперервної на відрізку  функції S(x),
функції S(x),  .
.
Виведемо формулу об’єму тіл обертання. Нехай криволінійна трапеція обмежена відрізком  осі абсцис, графіком функції y=f(x), невід’ємної і неперервної на вказаному відрізку, прямими х=а, х=b, обертається навколо осі абсцис. При обертанні цієї трапеції утворюється тіло, об’єм якого можна обчислити за формулою
осі абсцис, графіком функції y=f(x), невід’ємної і неперервної на вказаному відрізку, прямими х=а, х=b, обертається навколо осі абсцис. При обертанні цієї трапеції утворюється тіло, об’єм якого можна обчислити за формулою 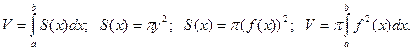
Таблиця: Площі плоских фігур.
На практиці доводиться обчислювати площі фігур, які не є криволінійними трапеціями. Щоб обчислити площу фігури, обмежену кількома лініями, то знаходять криволінійні трапеції, переріз або об’єднання яких є дана фігура, обчислюють площі кожної з них і знаходять суму або різницю площ цих
криволінійних трапецій.
Площа криволінійної трапеції
  y y=f(x) y y=f(x)
          a b х
a b х
| |||
    Обчислення площ Обчислення площ
 y=f(x) y=f(x)
   y=g(x) y=g(x) 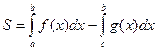 a c b x
a c b x
| |||
a b
y=f(x)
| |||
     y=f(x) y=g(x) y=f(x) y=g(x)
     
 a b c x a b c x
| |||
     y=f(x)
a b x y=f(x)
a b x       
 y=g(x) y=g(x)
|
Лекція 34: Інтеграл у фізиці та техніці. диференціальні рівняння.
План.
1. Інтеграл у фізиці та техніці:
-переміщення точки за проміжок часу;
-робота змінної сили;
-маса неоднорідного стержня;
-заряд, що проходить через поперечний переріз провідника за проміжок часу.
2.Поняття диференціального рівняння.
3.Диференціальне рівняння показникового зростання.
4.Диференціальне рівняння гармонічних коливань.
1. Інтеграл у фізиці та техніці.
Таблиця «Похідні та інтеграли у фізиці».
| № | величини | спів- відношення | похідна | інтеграл |
| S-переміщення v-швидкість | 
| 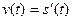
| 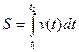
| |
| А-робота F-сила |  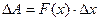
| 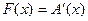
| 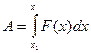
| |
| А-робота N-потужність | 
| 
| 
| |
 -маса стержня -маса стержня
 -густина -густина
| 
| 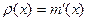
| 
| |
| q-електричний заряд І-сила струму | 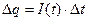
| 
| 
| |
| Q-кількість теплоти с-теплоємність | 
| 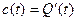
| 
|
1. Нехай точка рухається по прямій (вісь Ох) і ми знаємо швидкість точки. Як знайти переміщення точки за проміжок часу  ?
?
Розглянемо проміжок часу  і будемо вважати швидкість на цьому проміжку сталою, отже,
і будемо вважати швидкість на цьому проміжку сталою, отже,  , звідси
, звідси 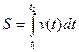 .
.
2.Нехай тіло рухається по осі ОХ, в кожній точці якої прикладена сила  . Обчислимо роботу, яку треба виконати при переміщенні із точки х1 в точку х2. На маленькому проміжку шляху від х до х+
. Обчислимо роботу, яку треба виконати при переміщенні із точки х1 в точку х2. На маленькому проміжку шляху від х до х+ 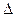 х вважаємо силу постійною, яка дорівнює
х вважаємо силу постійною, яка дорівнює  . Тоді
. Тоді 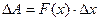 , отже,
, отже, 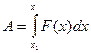 .
.
3.Розглянемо задачу обчислення маси неоднорідного стержня, якщо відома його густина  . Вважаючи, що на малому проміжку
. Вважаючи, що на малому проміжку 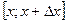 густина стала. маємо
густина стала. маємо  , тт.
, тт.  .
.
4.Поставимо задачу обчислити заряд q, що переноситься за проміжок часу  через переріз провідника. Нехай задано закон зміни струму
через переріз провідника. Нехай задано закон зміни струму  в залежності від часу. На малому проміжку часу
в залежності від часу. На малому проміжку часу  можна вважати силу струму постійною
можна вважати силу струму постійною 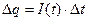 , отже,
, отже,  .
.
2.Поняття диференціального рівняння.
Задача про знаходження шляху  за заданою швидкістю
за заданою швидкістю  зводиться до розв’язування рівняння
зводиться до розв’язування рівняння  , де
, де  -задана функція,
-задана функція,  - шукана.
- шукана.
Це рівняння містить похідну невідомої функції. Такі рівняння називають диференціальними.
Наприклад: Розв’язати диференціальне рівняння 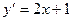 .
.
Розв’язання:
Треба знайти функцію, похідна якої дорівнює 2х+1, тт. знайти первісну функції 2х+1. 
Розв’язок диференціального рівняння визначається неоднозначно. До диференціального рівняння додається умова, із якої ця стала С визначається однозначно.
Наприклад: Знайти розв’язок диференціального рівняння  , у(0)=0.
, у(0)=0.
Розв’язання:

3.Диференціальне рівняння показникового зростання.
Розв’язування багатьох фізичних, біологічних, технічних задач зводиться до розв’язування диференціального рівняння 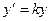 , к- задане число. Розв’язками цього рівняння є функції
, к- задане число. Розв’язками цього рівняння є функції 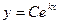 , С- стала, що визначається умовами задачі.
, С- стала, що визначається умовами задачі.
Задача: Швидкість  розмноження бактерій пов’язана з їх масою в момент часу
розмноження бактерій пов’язана з їх масою в момент часу 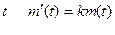 , де
, де 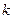 - додатне число, що залежить від виду бактерій і зовнішніх умов. Розв’язком цього рівняння є функція
- додатне число, що залежить від виду бактерій і зовнішніх умов. Розв’язком цього рівняння є функція  . С можна знайти з умови, що в момент часу
. С можна знайти з умови, що в момент часу  маса бактерій
маса бактерій 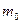 - відома. Тоді
- відома. Тоді 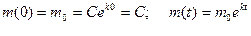 .
.
Задача: Якщо  -швидкість радіоактивного розпаду в момент часу
-швидкість радіоактивного розпаду в момент часу  , то
, то
 . де к –число, залежне від виду радіоактивної речовини. Розв’язком цього рівняння є функція
. де к –число, залежне від виду радіоактивної речовини. Розв’язком цього рівняння є функція  . Слід зазначити, що на практиці швидкість розпаду радіоактивної речовини характеризується періодом піврозпаду, тт. проміжком часу протягом якого розпадається половина даної речовини. Нехай Т- період піврозпаду, при t=T маємо
. Слід зазначити, що на практиці швидкість розпаду радіоактивної речовини характеризується періодом піврозпаду, тт. проміжком часу протягом якого розпадається половина даної речовини. Нехай Т- період піврозпаду, при t=T маємо  .
.
4.Диференціальне рівняння гармонічних коливань.
В житті часто зустрічаються процеси, які періодично повторюються: коливальний рух маятника, струни, пружини, процеси, пов’язані з електричним струмом, магнітним полем. Розв’язування цих задач зводиться до розв’язування рівняння  - задане додатне число,
- задане додатне число,  . Функцію
. Функцію  називають другою похідною функції у(х).
називають другою похідною функції у(х).
Розв’язком цього рівняння є функція  . Сталі числа С1 і С2 визначаються умовами конкретної задачі. Рівняння
. Сталі числа С1 і С2 визначаються умовами конкретної задачі. Рівняння 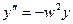 називають диференціальним рівнянням гармонічних коливань, а
називають диференціальним рівнянням гармонічних коливань, а  - розв’язком гармонічних коливань.
- розв’язком гармонічних коливань.
Таблиця «Похідні та інтеграли у фізиці».
| № | величини | спів- відношення | похідна | інтеграл |
| S-переміщення v-швидкість | 
| 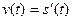
| 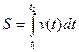
| |
| А-робота F-сила |  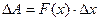
| 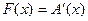
| 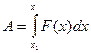
| |
| А-робота N-потужність | 
| 
| 
| |
 -маса стержня -маса стержня
 -густина -густина
| 
| 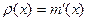
| 
| |
| q-електричний заряд І-сила струму | 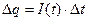
| 
| 
| |
| Q-кількість теплоти с-теплоємність | 
| 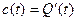
| 
|
1. Нехай точка рухається по прямій (вісь Ох) і ми знаємо швидкість точки. Як знайти переміщення точки за проміжок часу  ?
?
Розглянемо проміжок часу  і будемо вважати швидкість на цьому проміжку сталою, отже,
і будемо вважати швидкість на цьому проміжку сталою, отже,  , звідси
, звідси 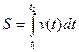 .
.
2.Нехай тіло рухається по осі ОХ, в кожній точці якої прикладена сила  . Обчислимо роботу, яку треба виконати при переміщенні із точки х1 в точку х2. На маленькому проміжку шляху від х до х+
. Обчислимо роботу, яку треба виконати при переміщенні із точки х1 в точку х2. На маленькому проміжку шляху від х до х+ 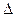 х вважаємо силу постійною, яка дорівнює
х вважаємо силу постійною, яка дорівнює  . Тоді
. Тоді 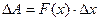 , отже,
, отже, 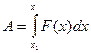 .
.
3.Розглянемо задачу обчислення маси неоднорідного стержня, якщо відома його густина  . Вважаючи, що на малому проміжку
. Вважаючи, що на малому проміжку 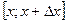 густина стала. маємо
густина стала. маємо  , тт.
, тт.  .
.
4.Поставимо задачу обчислити заряд q, що переноситься за проміжок часу  через переріз провідника. Нехай задано закон зміни струму
через переріз провідника. Нехай задано закон зміни струму  в залежності від часу. На малому проміжку часу
в залежності від часу. На малому проміжку часу  можна вважати силу струму постійною
можна вважати силу струму постійною 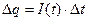 , отже,
, отже,  .
.
Лекція 35: Множини. Операції над множинами.
План.
1.Множина та її елементи.
2.Числові множини.
3.Множина комплексних чисел.
4.Порожня множина.
5.Способи задання множин.
6.Підмножина.
Під множиною в математиці розуміють сукупність деяких предметів чи об’єктів, що поєднані між собою деякою ознакою. множина, як математичне поняття не має означення. Множина – поняття первісне.
Наприклад: множина студентів групи.
Коли в математиці говорять про множину, то об’єднують деякі поняття чи предмети в одне ціле – множину, що складається з цих предметів. Засновник теорії множин Георг Кантор (1845-1918) виразив це такими словами: «Множина є об’єднання об’єктів, що мислиться як єдине ціле”.
Предмети, з яких складається множина, називаються її елементами. Для позначення множин використовують великі букви латинського алфавіту, а для позначення елементів-малі.
Якщо елемент належить множині позначають  , якщо – ні, то
, якщо – ні, то  .
.
Множину можна задати перерахуванням її елементів.
Наприклад: множина країн земної кулі.
Якщо множину задано списком, то вживають фігурні дужки для перерахування її елементів.
Не всі множини можна задати списком, якщо множина містить безліч елементів. Множина вважається заданою, якщо вказана властивість, яку мають всі її елементи і не мають цю властивість інші об’єкти. Така властивість називається характеристичною властивістю множини. Множину елементів, що мають характеристичну властивість позначають так: пишуть фігурні дужки, в них позначення елемента множини, після нього двокрапку, а потім – характеристичну властивість.
Наприклад:  означає, що множина А складається із всіх чисел, що задовольняють нерівність
означає, що множина А складається із всіх чисел, що задовольняють нерівність  .
.
Множина, що має певну кількість елементів (існує число, що виражає кількість елементів даної множини) називається скінченною, якщо множина має незліченну кількість елементів, то її називають нескінченною множиною.
Множину, яка не має жодного елемента називають порожньою.
Наприклад: множина перетину паралельних прямих.
Порожню множину позначають так:  Ǿ.
Ǿ.
Якщо кожен елемент множини В міститься в множині А, то множину В називають підмножиною множини А, і позначають так:  .
.
Наприклад: множина зірок нашої Галактики є підмножиною зірок Всесвіту.
Для математики важливу роль відіграють множини, що складаються з чисел, їх називають числові. Числові множини бувають  та комплексні числа С.
та комплексні числа С.


 Комплексні числа розглядаються як
Комплексні числа розглядаються як


 C розширення множини дійсних чисел.
C розширення множини дійсних чисел.
R
 | |||
 |
В Х\/І ст. на перших порах появи комплексні числа розглядались як засіб обчислень для знаходження дійсних коренів рівнянь ІІІ степеня.
2.Що таке уявна одиниця?
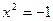 , число квадрат якого дорівнює 1, називається уявна одиниця і позначається х=і, отже, і2=-1.
, число квадрат якого дорівнює 1, називається уявна одиниця і позначається х=і, отже, і2=-1.
3.Запис комплексних чисел.
Вираз виду а+ві, де а і в- дійсні числа, а і – деякий символ, уявна одиниця називається комплексним числом.
Наприклад: 2+3і; -2-4і; -1+(-3)і.
а-дійсна частина, ві- уявна частина комплексного числа, в-коефіцієнт уявної частини.
Запис комплексного числа а+ві у вигляді суми дійсного числа а і чисто уявного числа ві називається алгебраїчною формою комплексного числа
a=Re z; b=Im z.
4.Рівні комплексні числа. Два комплексні числа називаються рівними, якщо рівні їх дійсні частини і коефіцієнти при уявних.
Якщо а+ві=с+dі, то а=с і в=d.
5.Спряжені комплексні числа.
Два комплексні числа а+ві та а-ві, у яких рівні дійсні частини, а коефіцієнти при уявних частинах-протилежні числа, називаються спряженими.
Наприклад: 7+8і та 7-8і.
6.Геометрична інтерпретація комплексних чисел.
Комплексні числа мають геометричну інтерпретацію. Кожному числу а+ві ставим у відповідність точку М(а;в) координатної площини. що називають комплексною, ОХ-її дійсна вісь, ОУ-уявна вісь.
Комплексне число а+ві можна розглядати як вектор  , де О(0;0), М(а;в).
, де О(0;0), М(а;в).
7.Дії над комплексними числами в алгебраїчній формі.
Для чисел z1=a+bі; z2=c+dі розглянемо арифметичні дії.
1) Додавання z1+z2=(a+bі)+(c+dі)= (a+c)+(b+d) і.
Наприклад: (2+(-1)і)+(-1+3і)=1+2і.
Властивості додавання-переставна і сполучна.
2) Віднімання z1-z2=(a+bі)-(c+dі)= (a-c)+(b-d) і.
Наприклад: (3+4і)-(1+2і)= (3-1)+(4-2)і=2+2і.
3) добуток z1z2=(a+bі)(c+dі)=ac+ad і+bc і+bd і2=(ac-bd)+(ad+bc) і.
Наприклад: (4-5і)(3+2і)=12+8і-15і+10=22-7і.
Властивості множення-комутативна, асоціативна, дистрибутивна.
4) Частка 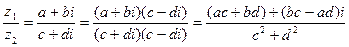 .
.
Наприклад:  .
.
5) Піднесення до степеня. Щоб піднести число і до степеня n ( ), треба показник степеня поділити на чотири і піднести і до степеня. Показник якого дорівнює остачі від ділення.
), треба показник степеня поділити на чотири і піднести і до степеня. Показник якого дорівнює остачі від ділення.
і0=1; і1=і; і2=-1; і3=і*і2=-і; і4=1.
Наприклад: і19=і3=-і.
6) Добування кореня квадратного з від’ємних чисел: 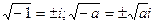 .
.
Лекція 36: Операції над множинами.
А
 АА
АА
В В

Перерізом множин А і В називається множина, що складається з усіх спільних елементів обох множин. Позначають 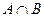 .
.
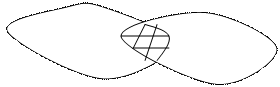 |
А В
Наприклад: А-множина прямокутників, В-множина ромбів, С-квадратів,

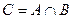 .
.
Об’єднанням множин А і В називають множину, що складається з усіх елементів, що входять хоча б до одної множини. Позначають  .
.
 |
А В
Наприклад: А-множина прямокутників, В-множина квадратів.  - множина прямокутників.
- множина прямокутників.
Різницею множин А і В називається множина всіх елементів А, що не входять до В. Позначається А\В.
 |
А В
Наприклад: А-множина студентів групи, В-множина дівчат, А\В- множина хлопців.
Лекція 37: Перестановки. Розміщення. Комбінації. Біном Ньютона.
Комбінаторика як наука займається дослідженням скінченних математичних структур, зокрема, множин. Під множиною розумітимемо сукупність об’єктів з певною ознакою.
Основні правила комбінаторики:
1.Якщо елемент а, що належить множині А, можна вибрати  способами із множини А, а елемент
способами із множини А, а елемент 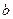 , що належить множині В, можна вибрати
, що належить множині В, можна вибрати  способами із множини В, то елемент Х, що належить одночасно обом множинам, можна вибрати
способами із множини В, то елемент Х, що належить одночасно обом множинам, можна вибрати  способами.
способами.
2.Якщо елемент а, що належить множині А, можна вибрати  способами із множини А, а елемент
способами із множини А, а елемент 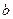 , що належить множині В, можна вибрати
, що належить множині В, можна вибрати  способами із множини В, то вибір пари
способами із множини В, то вибір пари  в указаному порядку можна виконати
в указаному порядку можна виконати 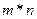 способами.
способами.
Поиск по сайту: