Экстраполяционные методы прогнозирования

Суть прогнозной экстраполяции заключается в нахождении закономерностей, присущих развитию объек­та в прошлом, и использовании этих закономерностей для построения прогноза.

Как уже было отмечено, инновационные процессы характеризуются нелинейностью и переломом сло­жившейся тенденции. По этой причине экстраполяционные методы непосредственно не могут быть использо­ваны для прогнозирования инноваций. В то же время без них практически невозможно обойтись при планиро­вании и прогнозировании поведения сложных систем. Прогноз значений отдельных параметров внешней среды, оперативный мониторинг - вот основные задачи, решаемые с помощью данной группы методов.

Методы прогнозной экстраполяции применимы к объектам, чьи характеристики имеют форму времен­ных (динамических) рядов.

В каждый момент времени на исследуемую характеристику воздействует большое количество факторов. Их совместное влияние формирует конкретное значение данного члена динамического ряда. Экстраполяцион­ные методы используют в том случае, когда нет возможности выявить существенные факторы и раздельно учесть влияние каждого из них. В общем случае, значение характеристики процесса в момент времени t можно представить выражением:

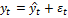, (2.2.3)

где 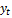– фактическое значение;

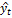– закономерная (неслучайная) составляющая;

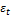– случайная составляющая.

Рассмотрим простейшие приемы прогнозирования, основанные на использовании средних характеристик динамического ряда.

Напомним, что существует ряд общепринятых показателей, характеризующих динамический ряд. Они могут быть трех видов: цепные; базисные; средние.

При расчете цепных показателей, каждый член ряда сравнивается с предыдущим, а при расчете базисных показателей члены ряда сравниваются с одним и тем же предшествующим уровнем, принятым за базу сравнения.

Среднее значение является как бы «типичным представителем» ряда и может быть вычислено как на ос­нове цепных, так и на основе базисных показателей. Средние значения могут быть использованы для приблизи­тельного («оценочного») прогнозирования исследуемой характеристики.

Рассмотрим основные средние показатели, характеризующие динамический ряд.

1) Средний уровень ряда:

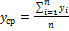, (2.2.4)

где n число членов ряда.

Этот показатель является «типичным представителем» стационарного ряда. Прогноз на к шагов вперед может быть рассчитан по формуле: .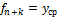

2) Средний абсолютный прирост:

(2.2.5)

где абсолютный прирост за период [t-1; t].

Процессы, характеризуемые постоянными приростами, могут быть описаны линейной функцией: 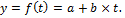Тогда – средняя скорость роста. Прогноз на k шагов перед может быть рассчитан по формуле: .

3) Средний цепной темп роста.

Цепной темп роста за период времени[t-1; t] равен:

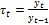(2.2.6)

Тогда для всего ряда получим соответствующий ряд цепных темпов роста: . Если бы все цепные темпы роста динамического ряда были бы одинаковы и равны , то, зная значение первого члена ряда , значения всех остальных можно было бы рассчитать по цепочке: Отсюда можно вывести фор­мулу для расчета среднего цепного темпа роста:

. (2.2.7)

Процессы, характеризуемые постоянным темпом роста и прироста, могут быть описаны экспоненциаль­ной функцией: , где b - мгновенный темп прироста. Прогноз на к шагов вперед может быть рассчитан по формуле: .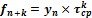

Средний цепной темп роста можно использовать для краткосрочного прогнозирования для получения приближенной точечной оценки характеристики процесса. Разумеется, такая оценка, строго говоря, не может считаться прогнозом. Но, тем не менее, этот метод, благодаря своей простоте и наглядности, часто используется именно с этой целью. Его применение может давать хорошие результаты при условии, если процесс развивается по экспоненте и период упреждения небольшой (один, два шага).

Главным недостатком метода является использование в расчетах только двух членов ряда - первого и по­следнего. От выбора этих значений может существенно зависеть точность прогноза. Указанный недостаток можно уменьшить, если в качестве первого и последнего членов ряда взять среднее значение соответственно нескольких первых и нескольких последних членов ряда. О достоверности (надежности) прогноза здесь гово­рить не приходится, поскольку нет возможности рассчитать доверительный интервал (прогноз точечный).

В экстраполяционном прогнозировании широкое применение находят различные методы сглаживания динамических рядов. Сглаживание динамических рядов используется, во-первых, для выявления общих тен­денций развития процессов. Во-вторых, эти процедуры лежат в основе многих методов краткосрочного прогно­зирования, как для условно-стационарных рядов, так и для нестационарных рядов.

Суть методов сглаживания заключается в замене фактических членов динамического ряда расчетными значениями, представляющими собой взвешенную сумму членов исходного ряда, т.е.:

, (2.2.8)

где 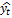– сглаженное значение члена ряда с номером t;

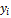– фактическое значение i-го члена ряда;

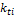– вес значимости i-го члена ряда, причем ;

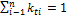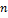– общее число членов исходного ряда.

Веса значимости {k_ti} характеризуют вклад каждого члена ряда в формирование нового (сглаженного) значения.

В результате этой процедуры мы получим новый динамический ряд {у_t}. Этот ряд отличается от исход­ного меньшим уровнем вариации, что говорит об уменьшении роли случайной составляющей в формировании значений ряда.

Рассмотрим два самых распространенных метода сглаживания:

♦ сглаживание по простой скользящей средней;

♦ сглаживание по экспоненциальной средней.

При сглаживании по простой скользящей средней сглаженное значение каждого члена ряда y_i рассчиты­вается как среднее арифметическое m ближайших к нему фактических значений, включая данное. Число m на­зывается периодом сглаживания.

Удобно брать нечетное значение периода сглаживания для того, чтобы номер сглаженного значения сов­падал с номером фактического значения. Например, m = 3, 5, 7, и т.д. Для удобства представим: m=2р+1.

Сглаженные значения рассчитывают по одной из двух формул:

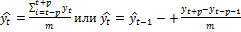. (2.2.9)

Метод сглаживания по простой скользящей средней имеет следующие особенности:

♦ члены ряда, участвующие в формировании сглаженного значения, имеют одинаковые веса, равные 1/m, остальные члены ряда - веса, равные нулю;

♦ степень сглаживания зависит от выбора константы т. Чем больше т, тем сильнее сглаживаются слу­чайные колебания, и выявляется общая тенденция развития процесса. С другой стороны, при большом т можно не заметить намечающегося изменения тенденции, а также сгладить неслучайные колебания, напри­мер, сезонные.

При краткосрочном прогнозировании для условно-стационарных рядов в качестве прогноза берут по­следнее сглаженное значение ряда: .

Недостатком данного метода является, во-первых, то, что в сглаживании участвуют не все члены ряда, а только т значений. Во-вторых, все эти значения имеют равные веса, хотя значимость более поздних наблюде­ний должна быть выше.

В методе сглаживания по экспоненциальной средней отсутствуют недостатки предыдущего метода. Во-первых, здесь в сглаживании участвуют все члены исходного ряда; во-вторых, более позднее наблюдение имеет вес, больший, чем у любого из предыдущих.

Прежде всего, необходимо выбрать параметр сглаживания а, который задает вес текущего наблюдения (0 < а < 1). Чем больше а, тем активнее текущее наблюдение влияет на результат сглаживание. На практике, наиболее часто выбирают а = 0,1; 0,2; 0,3. Сглаженное значение ряда u_t вычисляют по формуле:

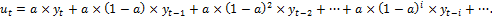(2.2.10)

Нетрудно заметить, что веса 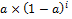с ростом i убывают по экспоненциальному закону, что и дало на­звание этому методу. Сумма весов стремится к 1.

Путем несложных подстановок можно получить итеративную формулу для расчета экспоненциальной средней:

(2.2.11)

В качестве и₀ можно выбрать, например, y₁ или среднее значение нескольких первых членов ряда. С уве­личением длины ряда вес и₀ будет быстро убывать, и этот член перестанет играть сколько-нибудь существенное значение в расчетах.

При краткосрочном прогнозировании характеристик, представленных условно-стационарными рядами значений, в качестве прогноза и_п+1 берут последнее сглаженное значение ряда и_n.

Метод экспоненциального сглаживания является более удобным и гибким по сравнению с методом сгла­живания по простой скользящей средней, поэтому он чаще используется на практике.

Формулу для расчета и_t можно преобразовать следующим образом:

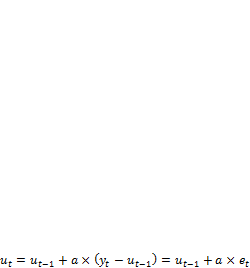, (2.2.12)

где е_t — ошибка прогноза.

На основе этой формулы предложен способ подбора параметра а, легко реализуемый с помощью ЭВМ. При этом способе рекомендуется брать такое значение а, которое минимизирует сумму квадратов ошибок {е_t}.

Метод экспоненциального сглаживания используется в прогнозировании не только для стационарных рядов, но и для рядов, чье среднее значение растет, уменьшается или подвержено сезонным колебаниям.

Рассмотрим методы адаптивного краткосрочного прогнозирования, использующие принцип сглаживания параметров.

Выделяют процессы, имеющие следующий характер:

♦ линейно-аддитивный;

♦ линейно-мультипликативный;

♦ сезонный.

Для линейно-аддитивных процессов характерно возрастание или убывание среднего значения характери­стики по линейному закону, т.е. абсолютные приросты за одинаковые промежутки времени остаются примерно одинаковыми.

Характер линейно-аддитивного процесса может быть выражен уравнением:

, (2.2.13)

где уt - фактическое значение характеристики в момент времени t;

— среднее процесса;

— скорость роста процесса;

— случайная ошибка.

Среднее процесса оценивается на каждом шаге значением , скорость роста — параметром , а про­гноз с периодом упреждения t рассчитывают по формуле:

, (2.2.14)

В методе адаптивного сглаживания Брауна для расчета значений , и , используют следующий способ, заключающийся в минимизации суммы взвешенных наименьших квадратов ошибок прогноза. Согласно этому способу:

(2.2.15)

где — вес ошибки в момент времени t - i.

Нетрудно заметить, что веса ошибок убывают с ростом срока их давности. На практике рекомендуется выбирать параметр = 0,8.

На основе использования метода взвешенных наименьших квадратов можно получить следующие итера­ционные уравнения для вычисления и :

(2.2.16)

; (2.2.17)

где - ошибка прогноза в момент времени t.

Выбор начальных значений , , и может осуществляться различными способами, например:

.

Кроме метода адаптивного сглаживания Брауна для краткосрочного прогнозирования линейно­аддитивных процессов используют и другие методы:

♦ метод Холта;

♦ метод Холта-Муира;

♦ метод двойного сглаживания Брауна;

♦ метод Бокса-Дженкинса.

Все эти методы приводят, в основном, к одним и тем же результатам. Однако практика показала, что ме­тод адаптивного сглаживания Брауна дает несколько более точный прогноз, по сравнению с остальными на­званными методами.

Линейно-мультипликативные процессы характеризуются линейным изменением во времени абсолютных приростов последовательных членов динамического ряда. Т.е. изменения значения показателя относительно среднего составляет за одинаковые промежутки времени примерно один и тот же процент. Абсолютное значе­ние случайной ошибки в среднем также возрастает с ростом среднего значения ряда.

Такая модель описывается уравнением:

, (2.2.18)

где y_t - фактическое значения характеристики в момент времени i.

e_t - мультипликативный коэффициент процесса;

p_t - значение случайной ошибки в момент времени t.

Разность (y_t-1 - e_t-1) представляет собой значение неслучайной составляющей характеристики в момент времени t - 1.

Метод Муира использует процедуру экспоненциального сглаживания для оценки параметров данного уравнения. При этом неслучайная составляющая оценивается значением и_t а параметр p_t значением r_t в соответ­ствии со следующими формулами:

, (2.2.19)

, (2.2.20)

где а - параметр экспоненциального сглаживания.

Начальные значения параметров могут быть выбраны следующим образом:

.

Тогда прогнозное значение характеристики с периодом упреждения вычислим по формуле:

(2.2.21)

Сезонный характер имеют процессы, отличающиеся циклическим изменением среднего значения в соот­ветствии с некоторым временным циклом. В большинстве случаев этот цикл равен одному году. Например, спрос на некоторые товары и услуги зависит от времени года (сезона).

Кроме чисто сезонных процессов, часто встречаются процессы, имеющие сезонно-линейный характер. При моделировании эти процессы рассматривают как комбинацию двух процессов - сезонного и линейного.

Сезонные колебания характеризуются коэффициентом сезонности. Коэффициент сезонности представля­ет собой отношение ожидаемого (прогнозируемого) значения показателя в данный момент времени к среднему значению этого показателя в соответствующие моменты времени для нескольких прошедших сезонных циклов. Желательно, чтобы число циклов при исследовании характеристик сезонности было не менее четырех.

Параметр L характеризует длину одного цикла. При годовом цикле: L = 12 (если измерение параметра производится раз в месяц).

Для прогнозирования процессов, которые можно представить комбинацией сезонной и линейно­аддитивной моделей, используется сезонно-декомпозиционная модель Холта—Винтера.

В этой модели необходимо оценить три фактора:

♦ среднее процесса (u_t);

♦ скорость роста (b_t);

♦ коэффициент сезонности (F_t).

Для нахождения соответствующих оценок используются следующие формулы:

, (2.2.22)

где - первый параметр экспоненциального сглаживания;

y_t — фактическое значение показателя в момент времени t;

F_t-L - оценка коэффициента сезонности на момент времени t - L, где L — длина цикла;

B_t-1 - оценка скорости роста в момент времени t - 1.

Оценка скорости роста:

, (2.2.23)

где a₂ — второй параметр экспоненциального сглаживания;

Оценка коэффициента сезонности:

, (2.2.24)

Где a₃ — третий параметр экспоненциального сглаживания;

y_t - фактическое значение показателя в момент времени t;

u_t - оценка среднего значения показателя в момент времени t;

F_t-_L - оценка коэффициента сезонности в момент времени t - L (предыдущий цикл), где L - длина цикла.

Тогда прогноз показателя у для периода упреждения а может быть рассчитан по формуле:

, (2.2.25)

В качестве параметров экспоненциального сглаживания а_}а2а₃ рекомендуется брать следующие значе­ния: a₁= 0,2; а₂ = 0,2; a₃ = 0,6.

Сезонно-декомпозиционная модель Холта-Винтера является самой простой из известных моделей данно­го типа, но, в то же время она не уступает другим моделям в прогностической точности.

Рассмотренные выше методы краткосрочного прогнозирования (в отличие от точечной оценки тенденций с помощью показателей динамики, таких, например, как средний цепной темп роста) могут быть проанализиро­ваны на предмет точности, надежности и практической значимости.

Напомним, что надежность (достоверность) прогноза задается уровнем требуемой доверительной веро­ятности Рдое.

Практическая значимость прогноза определяется шириной доверительного интервала прогноза при за­данной доверительной вероятности.

Точность прогноза - апостериорная характеристика степени близости реального значения к прогнозному.

При изучении социально-экономических процессов иногда бывает сложно выявить отдельные факторы, влияющие на изменение соответствующих показателей, или описать количественно характер этого влияния.

С другой стороны, в ходе развития процесса во времени могут наблюдаться устойчивые закономерности (тенденции), например, тенденция к росту, уменьшению или стабилизации значений показателя. В этом случае можно попытаться построить модель развития процесса в форме тренда.

Тренд это плавная кривая, описывающая в среднем изменение исследуемой характеристики во времени.

В общем случае значение показателя у в момент времени t можно представить в виде:

, (2.2.26)

где y_t = f(t) - значение неслучайной составляющей (тренда) в момент времени t;

е_t - реализация случайной составляющей в момент времени t.

Для аналитического описания формы тренда используют ряд простейших типовых функций, которые мы будем называть прогностическими. Перечислим самые распространенные из них:

Линейная функция: . Эта функция описывает процессы, характеризующиеся равномерным развитием во времени показателя у. Приросты показателя за равны промежутки времени одинаковы.

Парабола: . Процессы, описываемые этой функцией, отличаются неравномерным рос­том или спадом соответствующей характеристики в исследуемый период.

Экспонента: . Процессы, описываемые этой функцией, характеризуются ускоренным ростом или плавным затуханием соответствующего показателя у и постоянными темпами его роста (спада).

Степенная функция: . В зависимости от параметра b, процессы, описываемые этой функцией, характеризуются разной степенью неравномерности показателя во времени (ускоренный рост или спад).

Модифицированная экспонента: . Эта функция часто используется для описания процессов, характеризуемых насыщением, т.к. имеет асимптоту, равную k (уровень насыщения показателя у).

Логистическая кривая: . Эта кривая симметрична относительно точки перегиба и име­ет две асимптоты, равные к и 0. Также как и кривая Гомпертца используется для описания процессов, меняю­щих тенденцию и характеризуемых насыщением или затуханием.

Гипербола: . Кривая соответствует процессам с насыщением и (в зависимости от парамет­ра b) неравномерным ростом или спадом значений показателя у. Имеет асимптоту, равную а.

Логарифмическая кривая: . Данная кривая описывает процессы, приросты показателя кото­рых с течением времени убывают по логарифмическому закону.

Колебательная функция: Аналитическое выражение кривой включает в себя функции синуса и (или) ко­синуса. Если речь идет о кривой сезонности, описывающей изменение показателя в течение года, то аналитиче­ская форма кривой имеет вид ряда Фурье: , где k - номер гармоники ряда Фурье (k=1,2, 3,4).

Обычно, требуемая точность достигается применением первой гармоники (к = 1). Тогда уравнение имеет вид: . Поскольку в годовой динамике t означает номер месяца в году, то, исходя из величины (длина окружности), получим значения t, равные разным месяцам года.

Например, январь –t₁ =0; февраль -t₂ = /6; март -t₃ = /3 и т.д. (длина одного месяца равна /6).

Построение трендовой модели осуществляется в следующей последовательности:

♦ выбор формы кривой;

♦ оценка параметров;

♦ анализ качества модели.

Тренд в общем случае может быть описан комбинацией нескольких из рассмотренных выше прогности­ческих функций или, даже, одной из них.

Аналитическая форма кривой должна выбираться на основе качественного анализа исследуемого процес­са. Однако, на этом этапе может существовать некоторая неопределенность, не позволяющая сделать оконча­тельный выбор. Тогда рекомендуется использовать ряд формальных приемов для более четкого выявления за­кономерностей развития процесса. К ним относятся методы сглаживания динамических рядов и исключение нетипичных точек, появление которых явно связано либо с ошибками измерения, либо с маловероятным стече­нием обстоятельств. Если же этого недостаточно для решения вопроса о форме кривой, то можно использовать формальные методы, например, метод наименьших квадратов.

После того как проблема выбора формы тренда решена, необходимо найти (оценить) значения парамет­ров уравнения кривой на основе статистических данных, которые представлены в виде динамического ряда ис­следуемой характеристики у.

Но прежде, чем приступить к решению этой задачи, необходимо уяснить характер случайной состав­ляющей процесса - закон распределения и основные статистические показатели. При исследовании социально- экономических процессов, как правило, принимается следующая гипотеза: случайная составляющая подчиняет­ся нормальному закону распределения вероятностей с математическим ожиданием, равным нулю, постоянной дисперсией и независимостью любых двух последовательных значений друг от друга.

Можно доказать, что этим требованиям удовлетворяют оценки параметров, рассчитанных по методу наименьших квадратов. Этот метод заключается в подборе таких значений параметров, при которых сумма квадратов отклонений фактических значений динамического ряда от соответствующих значений, рассчитанных по уравнению кривой, была бы минимальной.

В том случае, если трендовая модель имеет форму нелинейной функции времени, система уравнений для нахождения параметров может получиться достаточно сложной. Метод наименьших квадратов в этом случае называют нелинейным методом наименьших квадратов, а при решении системы нелинейных уравнений исполь­зуют довольно трудоемкие математические методы.

Другой способ получения оценок параметров нелинейной модели заключается в приведении ее к линейно­му виду, посредством ряда несложных преобразований. Этот способ называется методом линеаризации модели.

Для получения оценок параметров линеаризованного уравнения применяют обычный метод наименьших квадратов, а затем осуществляют обратные преобразования.

Следует отметить, что линеаризация уравнения зачастую дает несколько смещенные оценки параметров (например, при логарифмировании). При высоких требованиях к точности следует пользоваться нелинейным методом наименьших квадратов.

После того как модель построена, необходимо оценить ее качество. Качество модели определяет ее при­годность для практического использования, т.е. степень адекватности реальному процессу.

Оценка качества модели включает: оценку значимости модели; анализ случайной составляющей.

Значимость трендовой модели определяется значимостью всех коэффициентов уравнения. Коэффициент считается значимым, если он существенно отличается от нуля.

Значимость коэффициента проверяется с помощью t-критерия Стьюдента. Расчеты, как правило, произво­дятся на ЭВМ.

Расчетное значение t-критерия (t_p) сравнивается со значением t_α, которое выбирается из соответствую­щей таблицы в зависимости от доверительной вероятности Р _дов, (или уровня значимости α = 1 - Р_дов) и числа степеней свободы v = п — т, где п — число наблюдений, a m - число параметров уравнения.

Если t_p>t_a, то коэффициент можно считать значимым с вероятностью Р_дов.

Рассмотрим пример: динамический ряд из 44 значений показателя у. Допустим, что для данного показа­теля построена модель в форме линейного тренда . Коэффициенты а и b рассчитаны по методу наи­меньших квадратов: а = 117,79; b = -0,2.

Тогда уравнение тренда: у = 117,79 - 0,2 t.

Расчетные значения t-критериев равны:

t_a = 194,48; t_b = 3,04.

Для доверительной вероятности Р_дов =0,95 (или уровня значимости 0,05) выбираем из таблицы значение критерия t_a для числа степеней свободы 42 (v = п - т = 44 - 2 - 42): t_α = 2,02.

Поскольку t_a> t_α и t_b> t_α, то оба коэффициента являются значимыми. Следовательно, значима сама ли­нейная модель.

Рассмотрим процедуру анализа случайной составляющей. Напомним, что случайная составляющая оце­нивается остатками {е_t} = {y_t-f(t)}

При анализе остатков проверяется выдвинутая выше гипотеза о том, какой характер должна иметь слу­чайная составляющая процесса.

Рассмотрим по порядку все перечисленные в этой гипотезе требования:

1) Нормальный закон распределения.

Подчиненность остатков нормальному закону распределения вероятностей может быть проверена целым рядом критериев, например, критерием Колмогорова. Но самый простой способ — визуальный, с помощью гис­тограммы.

2) Равенство нулю математического ожидания.

Это требование выполняется всегда, если для оценки параметров модели используется метод наимень­ших квадратов.

3) Постоянство дисперсии.

Постоянство дисперсии можно проверить с помощью критерия Фишера (F-критерия). Критерием Фише­ра исследуют гипотезу о равенстве двух дисперсий S₁ и S₂.

Если в качестве S₁ взять дисперсию первых п/2 членов ряда, а в качестве S₂ - дисперсию последних n/2 членов ряда, то с помощью F-критерия можно сделать вывод о равенстве или неравенстве этих дисперсий. Дис­персии рассчитываются по формулам:

Если F_p < F_a, то дисперсии S₁ и S₂ можно считать равными, и, следовательно, дисперсию остатков посто­янной. Здесь F_p и F_a — расчетное и табличное значения критерия, соответственно.

4) Отсутствие автокорреляции остатков.

Последнее требование к случайной составляющей состоит в том, что любые два ее последовательных значения должны быть независимы друг от друга (некоррелируемы). Это свойство проверяется с помощью кри­терия Дарбина-Уотсона.

Если с помощью критерия Дарбина-Уотсона мы обнаружили существенную автокорреляцию остатков, то следует пересмотреть решение о форме тренда.

Невыполнение хотя бы одного из рассмотренных выше требований к случайной составляющей говорит о непригодности построенной модели для практического использования.

Если мы смогли построить несколько моделей, оценка качества которых оказалась удовлетворительной, то дальнейшие исследования должны быть направлены на выбор наилучшей модели.

Формальный подход к решению этой проблемы состоит в следующем: наилучшей следует считать такую модель, для которой сумма квадратов остатков минимальна, по сравнению с другими моделями.

Часто используют и другие критерии: коэффициент корреляции и критерий Фишера. Однако, следует за­метить, что наилучшая модель, выбранная по критерию минимальной суммы квадратов остатков, окажется наи­лучшей и по другим упомянутым критериям.

Прогноз по трендовой модели строится в форме доверительного интервала. Среднее значение определя­ется по уравнению модели, а ширина доверительного интервала зависит от дисперсии случайной составляю­щей, периода упреждения и выбранной доверительной вероятности.

Например, доверительный интервал прогноза для линейного тренда на момент времени t_p может быть рассчитан по формуле:

, (2.2.27)

где S- среднеквадратическое отклонение остатков;

— значение, рассчитанное по уравнению тренда для момента времени t_p;

t_a — значение t-критерия Стьюдента, выбранное из таблицы для доверительной вероятности P_дов= 1 - а и числа степеней свободы v = n - 2;

n — количество наблюдений.

Поиск по сайту: