Случайные величины и законы их распределения

Случайной величиной называется величина, которая в результате опыта может принимать то или иное значение, но неизвестно заранее – какое именно.

Законом распределенияслучайной величины называется всякое соотношение, устанавливающее связь между возможными значениями этой величины и соответствующим им вероятностями. Пользуясь этим законом, можно рассчитать вероятность появления случайной величины, не выходящей по величине за определенные пределы, и наоборот – рассчитать значения пределов, внутри которых находится случайная величина с заданной вероятностью. Для дискретных (прерывных) случайных величин это могут быть функция распределения, ряд распределения, многоугольник распределения, а для непрерывных величин - функция распределения, плотность распределения, кривая распределения.

Числовой характеристикойслучайной величины называется параметр, в сжатой форме выражающий наиболее существенные особенности распределения данной случайной величины. Важнейшими из них являются: характеристика положения - математическое ожидание и характеристика рассеивания - дисперсия.

Математическим ожиданиемслучайной величины М(Х) называется центр рассеивания (среднее значение), около которого группируются возможные значения случайной величины x. Для дискретной случайной величины Х с частными значениями x_i и соответствующими им вероятностями p_i математическое ожидание равно_i:

Центрированной случайной величин ой называется отклонение случайной величины от ее математического ожидания:

.

Средним арифметическим значениемслучайной величины называется статистическая оценка математического ожидания при ограниченном количестве испытаний n:

.

Дисперсиейслучайной величины D(Х) называется математическое ожидание квадрата отклонения случайной величины x от его математического ожидания M(Х):

D(Х)=М[(x-M(Х)]²_,

Дисперсия характеризует степень разбросанности значений случайной величины относительно центра рассеивания (математического ожидания). Размерность дисперсии равна размерности квадрата случайной величины. Для дискретной случайной величины Х с частными значениями x_i и соответствующими им вероятностями p_i дисперсия равна:

;

Стандартом (стандартным отклонением) случайной величиныσ(Х) называется квадратный корень из дисперсии D(Х):

.

Он характеризует точность случайной величины, не зависит от количества измерений, а его размерность одинакова с размерностью случайной величины.

Среднеквадратической погрешностью ( СКП) случайной величины m(Х) называется статистическая оценка стандарта при ограниченном количестве n;

m(Х)=σ(Х) при n®¥.

Таким образом статистической оценкой истинного значения случайной величины X является его математическое ожидание М(Х) (среднее арифметическое значение x_ср), а статистической оценкой рассеивания случайной величины X – среднеквадратическая погрешность m(Х).

В судовождении используются следующие законы распределения:

- Нормальный закон распределения - наиболее часто встречающийся в практике судовождения закон распределения. Ему подчиняются абсолютное большинство случайных погрешностей измерений и вычислений навигационных величин;

- Закон равномерного распределения. В судовождении ему подчиняются погрешности снятия отсчетов со шкал приборов и погрешности округления чисел;

- Закон треугольника (закон Симпсона). В судовождении этому закону подчиняются погрешности выборки данных из таблиц;

- Закон распределения Рэлея. Ему подчиняются модули отклонений R случайной точки с координатами X и Y от начала координат, то есть длины случайного вектора с составляющимиX иY. В судовождении закон распределения Рэлея применяется для вычислении вероятности попадания случайной точкиС (места судна) при круговом ее распределении в круг заданного радиуса R_зад, центр которого совпадает с центром рассеивания;

- Закон распределения Стьюдента (закон t-распределения). В судовождении этот закон применяется для расчета математического ожидания, среднеквадратической погрешности,

величины доверительного интервала и доверительной вероятности при малом числе измерений (n<30).

- Закон распределения Смирнова (закон τ-распределения). В судовождении данный закон используются для выявления промахов при малом числе измерений (n<15) по критерию τ.

- Закон распределения размаха. В судовождении данный закон используются для выявления промахов при малом числе измерений (n<15) по размаху (разнице между максимальным х_max и минимальным х_min значениями случайной величины по результатам данной серии измерений);

- Закон распределения Фишера-Снедокора (закон F-распределения). В судовождении данный закон распределения используется для сравнения точности случайной величины, полученной в различных условиях.

- Закон χ²-распределения. В судовождении данный закон распределения используется для оценки того, насколько фактическое распределение рассматриваемой случайной величины Х соответствует тому или иному используемому для ее обработки закону распределения.

Если известно истинное значение навигационного параметра, то определение среднеквадратической погрешности его измерения выполняется способом абсолютной привязки:

,

где U_ист - истинное значение навигационного параметра;

U_i - результат измерения i - го навигационного параметра;

n - число измерений.

Если истинное значение измеряемого навигационного параметра неизвестно, то используется вероятнейшее значение U_внавигационного параметра.

За вероятнейшее значение U_визмеряемого навигационного параметра при равноточных наблюдениях принимают среднее арифметическое значение U_ср, определяемое по формуле:

;

Тогда определение среднеквадратической погрешности можно выполнить двумя способами:

- способом внутренней сходимости - по отклонению от вероятнейшего значения навигационного параметра;

- по размаху.

Среднеквадратическая погрешность единичного измерения навигационного параметра способом внутренней сходимости вычисляется по формуле Бесселя:

.

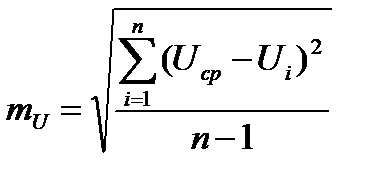Для получения СКП единичного измерения по размаху используется формула:

m_U=k_n×R

где R=U_max-U_min – размах, равный разности наибольшего и наименьшего из результатов измерений;

k_n - коэффициент, выбираемый из таблицы 4.5 МТ-2000 по числу измерений n.

Так как величины U_max и U_min случайные, следовательно и размах является случайной величиной. Он характеризует рассеивание измеренных величин.

Среднее арифметическое (вероятнейшее) значение навигационного параметра, полученное по ограниченному числу измерений, по сути также является случайной величиной. В общем случае оно содержит случайную погрешность, обусловленную неполной взаимной компенсацией случайных погрешностей отдельных измерений.

Среднеквадратическая погрешность вероятнейшего значения навигационного параметра m_Uв вычисляется по формуле:

.

При нормальном законе распределения случайных погрешностей вероятность того, что погрешность не выходит за пределы среднеквадратической погрешности m составляет 0,683 (68,3%).

Интервал, в пределах которого с заданной вероятностью находится истинное значение навигационного параметра, называется доверительным интервалом. Границы такого интервала называются доверительными границами. Вероятность того, что истинное значение навигационного параметра находится в заданном интервале, называется доверительной вероятностью Р.

Доверительный интервал, в пределах которого располагается истинное значение навигационного параметра с заданной вероятностью Р, определяется выражением:

U_в - t·m_Uв ≤ U_в ≤ U_в + t·m_Uв

В данном выражнии величина t есть некоторая безразмерная случайная величина. Если случайная величина U подчинена нормальному закону распределению, то величина t при малом числе измерений (n<30) подчинена распределению Стьюдента (t-распределению).

Величина t вычисляется по формуле:

;

где D_Uв - доверительный интервал.

При n<30 распределение Стьюдента значительно отличается от нормального, вследствие чего его роль особенно велика при анализе точности вероятнейших навигационных параметров, вычисленных по малому числу измерений. При ограниченном числе измерений использование нормального закона распределения неизбежно ведёт к завышению точности. При навигационных расчётах безопасности плавания завышение точности навигационной информации недопустимо. Поэтому в практических ситуациях для оценки надёжности вероятнейших навигационных параметров при малом числе измерений целесообразно пользоваться распределением Стьюдента.

Значения t, соответствующие различным Р и n, приведены в таблице 4.8 МТ-2000.

При n→∞распределение Стьюдента переходит в нормальное распределение, тогда t=z. При n≥30, или там, где не требуется высокая точность доверительных границ, доверительный интервал определяется выражением:

U_в - z·m_Uв ≤ U_в ≤ U_в + z·m_Uв,

где z – нормированная погрешность навигационного параметра:

.

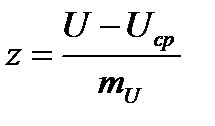Если в качестве доверительного интервала используется среднеквадратическая погрешность навигационного параметра m_U, тогда:

U_в - m_Uв ≤ U_в ≤ U_в +m_Uв

Неравноточными называются такие измерения, у которых различны их среднеквадратические погрешности. Такие измерения получаются тогда, когда они производятся в различных условиях, различными наблюдателями, различными по точности приборами или методами (например, в разных сериях производится различное количество наблюдений).

При обработке неравноточных измерений среднее арифметическое уже не будет являться вероятнейшим значением навигационного параметра, так как более точные измерения должны оказывать на конечный результат большее значение

Для обработки таких наблюдений используется численная величина, называемая весом наблюдений. Вес служит сравнительной оценкой качества отдельных или серии измерений. Если известна среднеквадратическая погрешность измерений, то вес является величиной, обратно пропорциональной квадрату среднеквадратической погрешности:

.

Вероятнейшим значением навигационного параметра U_в при неравноточных измерениях будет являться так называемое средневзвешенное (весовое среднее, весовая арифметическая середина) значение, которое вычисляется по формуле:

,

где U_i - результат i – го измерения;

p_i - вес i – го измерения;

n – количество измерений.

Таким образом при неравноточных измерениях вероятнейшее значение навигационного параметра U_в равно сумме произведений каждого результата измерений U_i на свой вес p_i, деленное на сумму весов всех измерений.

Иногда наименьший из весов p_i удобнее считать равным единице и вычислить веса остальных измерений относительно него.

Для оценки точности неравноточных измерений используется так называемая среднеквадратическая погрешность единицы веса, то есть среднеквадратическая погрешность такого измерения, вес которого принят за единицу.

Если истинное значение навигационного параметра неизвестно, то для вычисления среднеквадратической погрешности единицы веса m₍₁₎ используется формула:

,

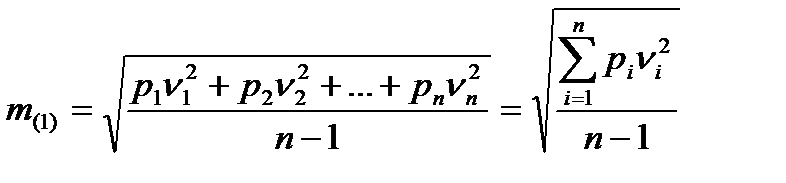где n_i - отклонение i-го измерения от вероятнейшего (средневзвешенного) значения:

n_i=U_в - U_i.

Среднеквадратическая погрешность вероятнейшего значения навигационного параметра m_Uв при неравноточных независимых наблюдениях вычисляется о формуле:

.

Среднеквадратическая погрешность единичного (отдельного) значения навигационного параметра m_Ui при неравноточных независимых наблюдениях вычисляется о формуле:

.

Поиск по сайту: