 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
ЛЕКЦИЯ 2 Синтез цифровых автоматов без памяти
Общая задача структурного синтеза комбинационных схем
Будем рассматривать синтез КС, реализующей одну ПФ. Процесс синтеза КС на элементах заданного базиса разбивается на следующие этапы:
1) Аналитическая запись ПФ в булевом базисе: в совершенной дизъюнктивной нормальной форме (СДНФ) или в совершенной дизъюнктивной нормальной форме (СКНФ).
2) Минимизация ПФ в булевом базисе.
3) Представление полученного после минимизации выражения в заданном базисе (переход к заданному базису).
4) Аналитическая запись ПФ в булевом базисе (запись в виде СДНФ или в СКНФ).
Минимизация ПФ в булевом базисе
Совершенные ДНФ и КНФ используются лишь для первоначального представления ПФ. Дело в том, что эти формы записи в ПФ не удобны для построения КС, поскольку при их реализации получаются схемы, содержащие элементы, которые можно исключить, если исходить из других форм ПФ. Поэтому при синтезе КС встает задача упрощения записи выражения для ПФ. Эта задача называется минимизацией ПФ.
В процессе минимизации СДНФ получается последовательно в начале сокращенная ДНФ, далее тупиковая и минимальная.
Существуют различные методы минимизации ПФ, из которых чаще всего используются методы Квайна, Мак-Класки, Блейка-Порецкого, диаграмм Вейча и карт Карно. В принципе все эти методы являются равновидностями метода Квайна.
Метод минимизации Блейка-Порецкого
Недостатком метода Квайна является то, что для его применения необходимо представить функцию в СДНФ. Процесс такого представления для функции с большим числом аргументов зачастую является весьма громоздкой задачей, т.е. было бы желательно найти возможность построения сокращенной ДНФ не по СДНФ, а по произвольной ДНФ данной функции. Идея построения сокращенной ДНФ по произвольной ДНФ была предложена в работах А. Блейка и П.С. Порецкого. Суть метода состоит в том, что в произвольной ДНФ осуществляют все операции обобщенного склеивания.
Если в ДНФ для данной функции f(А, В, С) входят две конъюнкции вида АС и B  , то имеет место следующее равенство:
, то имеет место следующее равенство:

Запишем функцию f (А, В, С) в следующем виде:

Из этого вытекает метод построения сокращенной ДНФ. Этот метод заключается в том, что если в ПФ есть конъюнкции с переменными С и  , то не изменяя исходную функцию необходимо пополнить ее новыми членами вида АВ. После этого надо провести поглощения и вновь повторить пополнение ДНФ. Этот процесс необходимо производить до тех пор, пока не будут возникать новые конъюнкции вида АВ. По окончании преобразований получаем сокращенную ДНФ.
, то не изменяя исходную функцию необходимо пополнить ее новыми членами вида АВ. После этого надо провести поглощения и вновь повторить пополнение ДНФ. Этот процесс необходимо производить до тех пор, пока не будут возникать новые конъюнкции вида АВ. По окончании преобразований получаем сокращенную ДНФ.
Пример 2.3. Найти сокращенную ДНФ для функции 3-х аргументов:

Метод минимизации Мак-Класки
В методе Квайна есть одно существенное неудобство. Оно связано с необходимостью полного попарного сравнения всех членов СДНФ ПФ на этапе нахождения всех простых импликант (при выполнении всевозможных операций неполного склеивания). При большом числе переменных применение метода Квайна становится затруднительным. Мак-Класки предложил модернизацию метода Квайна, дающую уменьшение числа сравнений.
Идея метода Мак-Класки заключается в следующем: конституенты 1 в СДНФ представляются не в буквенном виде, а виде условных чисел – номеров соответствующих конституент.
Пример 2.4. 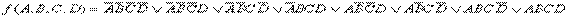 =
=
= 0000  0001
0001  0010
0010  0111
0111  1001
1001  1010
1010  1110
1110  1111 =
1111 =
= 0  1
1  2
2  7
7  9
9  10
10  14
14  15 =
15 =  (0, 1, 2, 7, 9, 10, 14, 15).
(0, 1, 2, 7, 9, 10, 14, 15).
При этом оказывается, что переменные имеют вес: ABCD  8421.
8421.
Давайте посмотрим, какие конституенты 1 склеиваются. Мы говорили, что могут склеиваться те, у которых число отрицаний отличается на 1.
 = 0000
= 0000  0001 = 0
0001 = 0  1=
1=  ; 0
; 0  1 = (0, 1), (1), т.е. склеиваются конституенты 0 и 1, а в скобках указывается разность, какая переменная исключается (D).
1 = (0, 1), (1), т.е. склеиваются конституенты 0 и 1, а в скобках указывается разность, какая переменная исключается (D).
Еще пример: 0100  0110 = 4
0110 = 4  6 = (4, 6), (2) – склеиваются по C.
6 = (4, 6), (2) – склеиваются по C.
Вводится понятие индекса. Индексом целого числа называется количество 1 в двоичном представлении этого числа: 7 = 0111 – индекс равен 3, 0000 – индекс равен 0 и т.д. Если конституенты 1 склеиваются, то их индексы отличаются на 1, а в скобках должно быть число (их разности), равное целой степени 2 (по какой переменной склеиваются).
Правило. Для того чтобы два числа m и n являлись номерами двух склеивающихся между собой конституент 1, необходимо и достаточно, чтобы их индексы отличались точно на 1, чтобы сами числа отличались друг от друга на степень 2, и чтобы число с большим индексом было больше числа с меньшим индексом.
Так конституенты 1 с номерами 4 и 3, равными 0100 и 0011, не склеиваются, хотя их разности равны 1.
Все конституенты 1 разбиваются на группы в соответствии с индексом и располагаются в порядке их возрастания. Группы отделяются друг от друга чертой. Склеиваться могут конституенты только соседних групп.
Пример 2.5.  (0, 1, 3, 4, 5, 6, 10, 11, 12, 14, 15). Минимизировать методом Мак-Класки.
(0, 1, 3, 4, 5, 6, 10, 11, 12, 14, 15). Минимизировать методом Мак-Класки.
Прежде всего группируем номера конституент в порядке роста их индексов. В нулевую группу попадает номер 0. В 1 группу – конституенты с индексом 1 (1 и 4), во 2 группу – конституенты с индексом 2 (3 = 0011, 5 = 0101, 6 = 0110, 10 = 1010 и 12 = 1100), в 3 группу – конституенты с индексом 3 (11 = 1011 и 14 = 1110), в 4 группу – конституенты с индексом 4 (15 = 1111). В результате имеем следующее разбиение конституент функции  на группы:
на группы:
В силу рассмотренного правила, склеивание возможно между номерами конституент соседних групп, т.е. 0 и 1, 1 и 2, 2 и 3 и 3 и 4. Никакие другие склеивания невозможны. Необходимо также, чтобы число, стоящее в следующей группе, было больше соответствующего числа в предыдущей группе, причем больше на целую степень 2. Например, 0 склеивается с 1, записывается пара (0,1) и рядом их разность: 1 – 0 = 1. Запись выглядит так: (0, 1), (1).
Около склеенных номеров ставятся звездочки, показывающие, что эти члены участвовали хотя бы в одном склеивании. Такие члены, как известно, в сокращенную ДНФ уже не войдут. После завершения склеивания групп отделяем горизонтальной чертой полученные выражения.
Дальше осуществляется та же процедура, но теперь склеиваются между собой полученные пары. Под парой подразумевается трехбуквенное выражение.
| 1 * 4 * | |
| 3 * 5 * 6 * 10 * 12 * | |
| 11 * 14 * | |
| 15 * |
| (0,1), | (1) * | (0,1,4,5), | (1,4) (с) | |
| (0,4), | (4) * | |||
| (1,3), | (2) (а) | (4,6,12,14), | (2,8) (d) | |
| (1,5), | (4) * | |||
| (4,5), | (1) * | (10,11,14,15) | (1,4) (e) | |
| (4,6), | (2) * | |||
| (4,12), | (8) * | |||
| (3,11), | (8) (в) | |||
| (6,14), | (8) * | |||
| (10,11), | (1) * | |||
| (10,14), | (4) * | |||
| (12,14), | (2) * | |||
| (11,15), | (4) * | |||
| (14,15), | (1) * |
Для склеивания пар применяются те же правила, но добавляется еще одно условие: разности у склеиваемых пар должны быть одинаковы. При этом оказывается, что в парах переменные в выражении одинаковы.
Возьмем, например, пары (0, 1),(1) и (1, 3), (2). 0 и 1 склеиваются, 1 и 3 тоже, но разности у них не одинаковы – поэтому склеивание невозможно (у первой пары нет переменной D, у второй пары нет переменной С – они, конечно, и не могут склеиваться). В результате склеивания пишем уже четверки (0, 1, 4, 5) и две разности (1, 4), т.е. в результирующем выражении нет 2-х переменных B и D. После завершения этих склеиваний получают, если возможно, восьмерки, при этом должны совпадать уже разности в скобках у четверок и т.д.
Обозначим пары и четверки, которые не участвовали в склеивании, латинскими буквами. Тогда  . При получении выражения для импликант а, в, с и т.д., поступают следующим образом: берут любую из конституент 1, участвующих в операции склеивания, и исключают переменные, указанные в разностях. Например, для импликанты а получим: 0001=
. При получении выражения для импликант а, в, с и т.д., поступают следующим образом: берут любую из конституент 1, участвующих в операции склеивания, и исключают переменные, указанные в разностях. Например, для импликанты а получим: 0001= 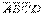 (разность 2). Эта разность говорит о том, из выражения необходимо исключить переменную с весом 2, т.е. С. Тогда а =
(разность 2). Эта разность говорит о том, из выражения необходимо исключить переменную с весом 2, т.е. С. Тогда а =  .
.
Аналогично получим: для в: 0011=  (разность 8), в =
(разность 8), в = 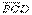 , для с: 0001=
, для с: 0001= 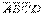 (разности 1 и 4), с =
(разности 1 и 4), с =  , для d: 0100 =
, для d: 0100 =  (разности 2 и 8), d =
(разности 2 и 8), d = 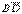 , для e: 1111=AВCD (разности 1 и 4), e = АС. В результате получим:
, для e: 1111=AВCD (разности 1 и 4), e = АС. В результате получим:  .
.
Метод диаграмм Вейча или карт Карно
Методы Квайна и Блейка-Порецкого являются аналитическими. В этих методах наиболее трудоемким является процесс отыскания склеивающихся между собой конъюнкций. Существуют методы, которые позволяют упростить поиск склеивающихся членов. Один из наиболее удобных методов минимизации ПФ от небольшого числа переменных основан на использовании диаграмм Вейча или карт Карно. Диаграмма Вейча представляет собой фактически таблицу истинности ПФ, которая представляется не в виде столбцов, а в виде специальных карт. Каждой клетке диаграммы соответствует определенный набор значений аргументов. Поэтому диаграммы можно рассматривать как графическое представление совокупности всех конституент единицы. При этом диаграмма строится таким образом, что склеивающиеся между собой конституенты оказываются расположенными в соседних клетках, т.к. отличаются значением только одной переменной. Приведем примеры построения диаграммы Вейча и карт Карно для ПФ от разного числа аргументов.
Метод минимизации Мак-Класки
В методе Квайна есть одно существенное неудобство. Оно связано с необходимостью полного попарного сравнения всех членов СДНФ ПФ на этапе нахождения всех простых импликант (при выполнении всевозможных операций неполного склеивания). При большом числе переменных применение метода Квайна становится затруднительным. Мак-Класки предложил модернизацию метода Квайна, дающую уменьшение числа сравнений.
Идея метода Мак-Класки заключается в следующем: конституенты 1 в СДНФ представляются не в буквенном виде, а виде условных чисел – номеров соответствующих конституент.
Пример 2.4. 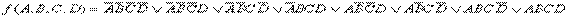 =
=
= 0000  0001
0001  0010
0010  0111
0111  1001
1001  1010
1010  1110
1110  1111 =
1111 =
= 0  1
1  2
2  7
7  9
9  10
10  14
14  15 =
15 =  (0, 1, 2, 7, 9, 10, 14, 15).
(0, 1, 2, 7, 9, 10, 14, 15).
При этом оказывается, что переменные имеют вес: ABCD  8421.
8421.
Давайте посмотрим, какие конституенты 1 склеиваются. Мы говорили, что могут склеиваться те, у которых число отрицаний отличается на 1.
 = 0000
= 0000  0001 = 0
0001 = 0  1=
1=  ; 0
; 0  1 = (0, 1), (1), т.е. склеиваются конституенты 0 и 1, а в скобках указывается разность, какая переменная исключается (D).
1 = (0, 1), (1), т.е. склеиваются конституенты 0 и 1, а в скобках указывается разность, какая переменная исключается (D).
Еще пример: 0100  0110 = 4
0110 = 4  6 = (4, 6), (2) – склеиваются по C.
6 = (4, 6), (2) – склеиваются по C.
Вводится понятие индекса. Индексом целого числа называется количество 1 в двоичном представлении этого числа: 7 = 0111 – индекс равен 3, 0000 – индекс равен 0 и т.д. Если конституенты 1 склеиваются, то их индексы отличаются на 1, а в скобках должно быть число (их разности), равное целой степени 2 (по какой переменной склеиваются).
Правило. Для того чтобы два числа m и n являлись номерами двух склеивающихся между собой конституент 1, необходимо и достаточно, чтобы их индексы отличались точно на 1, чтобы сами числа отличались друг от друга на степень 2, и чтобы число с большим индексом было больше числа с меньшим индексом.
Так конституенты 1 с номерами 4 и 3, равными 0100 и 0011, не склеиваются, хотя их разности равны 1.
Все конституенты 1 разбиваются на группы в соответствии с индексом и располагаются в порядке их возрастания. Группы отделяются друг от друга чертой. Склеиваться могут конституенты только соседних групп.
Пример 2.5.  (0, 1, 3, 4, 5, 6, 10, 11, 12, 14, 15). Минимизировать методом Мак-Класки.
(0, 1, 3, 4, 5, 6, 10, 11, 12, 14, 15). Минимизировать методом Мак-Класки.
Прежде всего группируем номера конституент в порядке роста их индексов. В нулевую группу попадает номер 0. В 1 группу – конституенты с индексом 1 (1 и 4), во 2 группу – конституенты с индексом 2 (3 = 0011, 5 = 0101, 6 = 0110, 10 = 1010 и 12 = 1100), в 3 группу – конституенты с индексом 3 (11 = 1011 и 14 = 1110), в 4 группу – конституенты с индексом 4 (15 = 1111). В результате имеем следующее разбиение конституент функции  на группы:
на группы:
В силу рассмотренного правила, склеивание возможно между номерами конституент соседних групп, т.е. 0 и 1, 1 и 2, 2 и 3 и 3 и 4. Никакие другие склеивания невозможны. Необходимо также, чтобы число, стоящее в следующей группе, было больше соответствующего числа в предыдущей группе, причем больше на целую степень 2. Например, 0 склеивается с 1, записывается пара (0,1) и рядом их разность: 1 – 0 = 1. Запись выглядит так: (0, 1), (1).
Около склеенных номеров ставятся звездочки, показывающие, что эти члены участвовали хотя бы в одном склеивании. Такие члены, как известно, в сокращенную ДНФ уже не войдут. После завершения склеивания групп отделяем горизонтальной чертой полученные выражения.
Дальше осуществляется та же процедура, но теперь склеиваются между собой полученные пары. Под парой подразумевается трехбуквенное выражение.
| 1 * 4 * | |
| 3 * 5 * 6 * 10 * 12 * | |
| 11 * 14 * | |
| 15 * |
| (0,1), | (1) * | (0,1,4,5), | (1,4) (с) | |
| (0,4), | (4) * | |||
| (1,3), | (2) (а) | (4,6,12,14), | (2,8) (d) | |
| (1,5), | (4) * | |||
| (4,5), | (1) * | (10,11,14,15) | (1,4) (e) | |
| (4,6), | (2) * | |||
| (4,12), | (8) * | |||
| (3,11), | (8) (в) | |||
| (6,14), | (8) * | |||
| (10,11), | (1) * | |||
| (10,14), | (4) * | |||
| (12,14), | (2) * | |||
| (11,15), | (4) * | |||
| (14,15), | (1) * |
Для склеивания пар применяются те же правила, но добавляется еще одно условие: разности у склеиваемых пар должны быть одинаковы. При этом оказывается, что в парах переменные в выражении одинаковы.
Возьмем, например, пары (0, 1),(1) и (1, 3), (2). 0 и 1 склеиваются, 1 и 3 тоже, но разности у них не одинаковы – поэтому склеивание невозможно (у первой пары нет переменной D, у второй пары нет переменной С – они, конечно, и не могут склеиваться). В результате склеивания пишем уже четверки (0, 1, 4, 5) и две разности (1, 4), т.е. в результирующем выражении нет 2-х переменных B и D. После завершения этих склеиваний получают, если возможно, восьмерки, при этом должны совпадать уже разности в скобках у четверок и т.д.
Обозначим пары и четверки, которые не участвовали в склеивании, латинскими буквами. Тогда  . При получении выражения для импликант а, в, с и т.д., поступают следующим образом: берут любую из конституент 1, участвующих в операции склеивания, и исключают переменные, указанные в разностях. Например, для импликанты а получим: 0001=
. При получении выражения для импликант а, в, с и т.д., поступают следующим образом: берут любую из конституент 1, участвующих в операции склеивания, и исключают переменные, указанные в разностях. Например, для импликанты а получим: 0001= 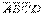 (разность 2). Эта разность говорит о том, из выражения необходимо исключить переменную с весом 2, т.е. С. Тогда а =
(разность 2). Эта разность говорит о том, из выражения необходимо исключить переменную с весом 2, т.е. С. Тогда а =  .
.
Аналогично получим: для в: 0011=  (разность 8), в =
(разность 8), в = 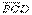 , для с: 0001=
, для с: 0001= 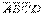 (разности 1 и 4), с =
(разности 1 и 4), с =  , для d: 0100 =
, для d: 0100 =  (разности 2 и 8), d =
(разности 2 и 8), d = 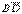 , для e: 1111=AВCD (разности 1 и 4), e = АС. В результате получим:
, для e: 1111=AВCD (разности 1 и 4), e = АС. В результате получим:  .
.
Переключательные функции трех аргументов
Пример 2.7.  .
.
Диаграмма Вейча состоит из 8 клеток и имеет следующий вид:

Тогда  .
.
В этой карте соседними клетками являются также крайние клетки каждой строки, т.к. расположенные в них конституенты отличаются друг от друга значением только одной переменной. Такую диаграмму следует рассматривать как свернутую в цилиндр.
Минимизация ПФ с помощью диаграмм Вейча и карт Карно сводится к такому объединению соседних единиц в группы, при котором каждая группа содержит максимальное число единиц, а количество таких групп минимально. При этом все единицы диаграммы Вейча данной функции накрываются наименьшим числом наиболее коротких произведений (импликант).
Переключательные функции четырех аргументов
В диаграммах Вейча и картах Карно для четырех аргументов соседними клетками являются крайние клетки каждого столбца и строки. Поэтому такую диаграмму следует рассматривать как свернутую в тор.
Пример 2.8.  (0, 1, 4, 5, 9, 10, 11, 13, 14, 15).
(0, 1, 4, 5, 9, 10, 11, 13, 14, 15).
Диаграмма Вейча состоит из 16 клеток и имеет следующий вид:


Построим схему в булевом базисе (рис. 2.1):

Рис. 2.1
Построим схему, реализующую функции  в базисе И-НЕ (штрих Шеффера). Для этого осуществим переход от булевого базиса к базису И-НЕ:
в базисе И-НЕ (штрих Шеффера). Для этого осуществим переход от булевого базиса к базису И-НЕ:
Схема, реализующая функцию  в базисе И-НЕ, приведена на рис. 2.2.
в базисе И-НЕ, приведена на рис. 2.2.

Рис. 2.2
Построим схему, реализующую функции  в базисе ИЛИ-НЕ (стрелка Пирса). Для этого осуществим переход от булевого базиса к базису ИЛИ-НЕ:
в базисе ИЛИ-НЕ (стрелка Пирса). Для этого осуществим переход от булевого базиса к базису ИЛИ-НЕ:
Схема, реализующая функцию  в базисе ИЛИ-НЕ, приведена на рис. 2.3.
в базисе ИЛИ-НЕ, приведена на рис. 2.3.

Рис. 2.3
Контрольные вопросы к лекции 2:
1.Что такое «логический элемент»?
2.Назовите основные параметры ЛЭ.
3.Что такое коэффициент объединения?
4.Зачем производят разделение входов?
5.Что такое нагрузочная способность ЛЭ?
6.Как выполняется разгрузка ЛЭ?
7.Как избежать увеличения задержки сигнала при разгрузке ЛЭ?
8.Назовите элементы булева базиса.
Поиск по сайту: