 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Формулы сокращенного умножения
МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ
ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
ГРАЖДАНСКОЙ АВИАЦИИ
Е.А. Жукова, Л.Д. Жулева
НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
Справочный материал и пособие к практическим занятиям и СРС
для студентов 1 и 2 курсов
всех специальностей и форм обучения
Москва 2012
Ø Первообразная и неопределённый интеграл
Функция F(x) называется первообразной для функции f(x) на (a,b), если F/(x)=f(x) на (a,b).
Множество всех первообразных для функции f(x) называется неопределенным интегралом и обозначается  .
.
Основные свойства неопределенного интеграла
1. 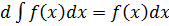
2. 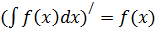
3. 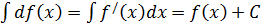
4. 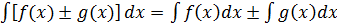
5. 
6. Если  и U=U(x), где U(x)- непрерывно дифференцируемая функция, то
и U=U(x), где U(x)- непрерывно дифференцируемая функция, то 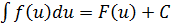
7. Если x=x(t) непрерывно дифференцируемая функция, то 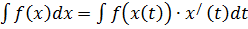 .
.
Таблица 1
Таблица простейших часто встречающихся интегралов
1. 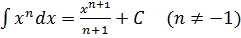 2.
2. 
3.  4.
4. 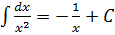
5. 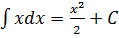 6.
6. 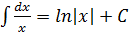
7. 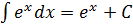 8.
8. 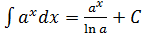
9. 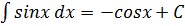 10.
10. 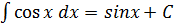
11. 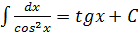 12.
12. 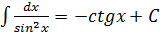
13. 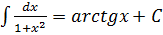 14.
14. 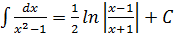
15. 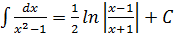 16.
16. 
17. 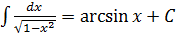 18.
18. 
При применении свойств 6 и 7 полезно использовать табл. 2.
Таблица 2
Таблица основных дифференциалов
1. 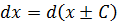

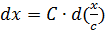 где С-константа.
где С-константа.
2. 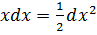 9.
9. 
3. 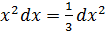 10.
10. 
4. 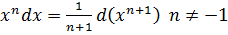 11.
11. 
5. 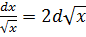 12.
12. 
6.  13.
13. 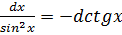
7.  14.
14. 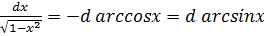
8. 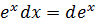 15.
15. 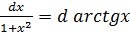
Рассмотрим примеры нахождения неопределенного интеграла методом «подведения под знак дифференциала», т.е. будем использовать табл. 2.
Пример 1
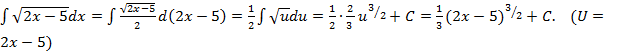 .
.
Пример 2
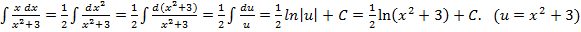 .
.
Пример 3
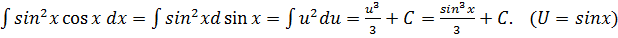 .
.
Пример 4
 .
.
Ø Интегрирование путем замены переменной
Один из наиболее распространенных методов, применяемых при вычислении неопределенных интегралов, метод замены переменных или подстановки.
Если известно, что 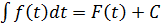 , то
, то
 где f(t), u(x), u/ (x) – непрерывны.
где f(t), u(x), u/ (x) – непрерывны.
Способ подстановки состоит в том, что сообразно виду подынтегральной функции составляют вспомогательную функцию, подстановка которой в исходный интеграл приводит его к виду более удобному для интегрирования (часто табличному).
Рассмотрим примеры, уже решенные ранее:
Пример 1
 .
.
Пример 2
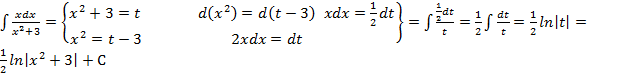 .
.
Пример 3
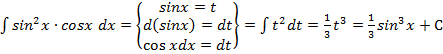 .
.
Пример 4
 .
.
Используем замену в более сложных примерах.
Пример 5

В этом случае используется форма подстановки, а именно  , получим
, получим
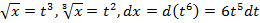
и 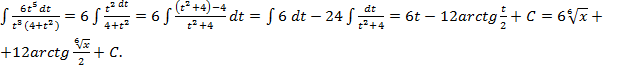
Пример 6
Использование универсальной тригонометрической подстановки
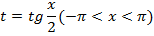

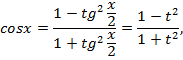
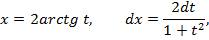
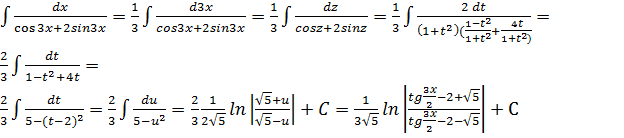 .
.
Метод замены переменной является одним из общих методов интегрирования. Умения использовать такие подстановки, которые упрощают подынтегральные выражения, вырабатываются практикой. Общих указаний по выбору выгодной подстановки дать нельзя.
Ø Интегрирование по частям
Пусть 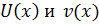 непрерывно дифференцируемые функции, тогда
непрерывно дифференцируемые функции, тогда 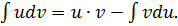 или
или 
Пример 7
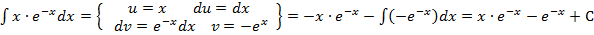 .
.
Пример 8
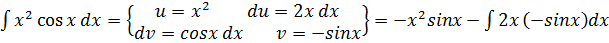 .
.
Рассмотрим получившийся интеграл
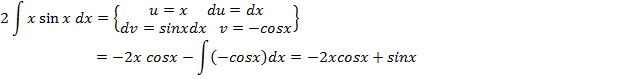
Ответ: 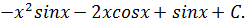
Замечания
Метод интегрирования по частям применяется при интегрировании следующих видов функций. 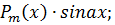

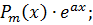
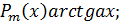
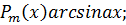
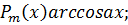
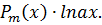
1. При интегрировании функций вида 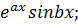
 интегрирование по частям применяется 2 раза, что приводит к решению уравнения для получения конечного ответа.
интегрирование по частям применяется 2 раза, что приводит к решению уравнения для получения конечного ответа.
Пример 9
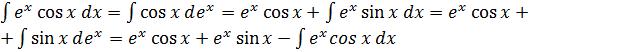 .
.
Пусть  .
.
Тогда последнее равенство может быть переписано в виде
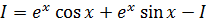 .
.
Получим уравнение

Отсюда
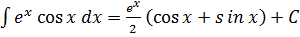 .
.
2. Метод интегрирования по частям может быть использован при интегрировании функций 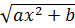 , тогда
, тогда 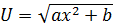 ,
, 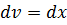 .
.
Пример 10
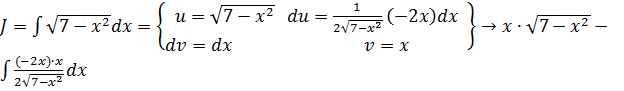 .
.
Рассмотрим получившийся интеграл.
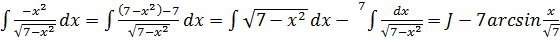 .
.
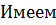 :
: 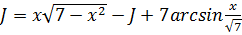 уравнение относительно J.
уравнение относительно J.
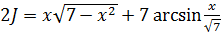 .
.
Ответ:
 .
.
Пример 10 может быть решен методом замены.
Пусть 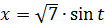 , тогда
, тогда 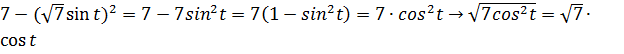 .
.
 .
.
 .
.
При вычислении одного и того же интеграла разными методами могут получаться отличные друг от друга ответы. Здесь имеем две функции 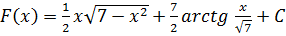 и
и  . Однако
. Однако 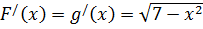
Предлагается проверить самостоятельно.
3. Необходимо иметь в виду, что применение метода интегрирования по частям приводит к частичному интегрированию, т.к. правая часть формулы (1) содержит интеграл. Но при правильном применении метода этот интеграл получается табличным или просто приводящимся к табличному.
Если в результате применения метода интегрирования по частям в правой части получается интеграл сложнее исходного, необходимо заново применить этот метод, разбив подынтегральное выражение на другие два множителя U и dV, из которых первый дифференцируется, а второй интегрируется при переходе к интегралу в правой части.
Умения правильного использования этого метода приобретаются только в результате упражнений.
Ø Интегрирование дробно-рациональных выражений
1. 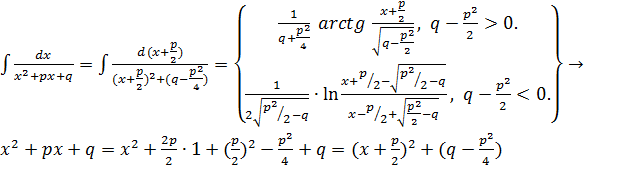 .
.
2. 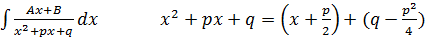 , причем, как предполагалось выше,
, причем, как предполагалось выше,  .
.
Обозначим: 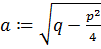 .
.
Сделаем замену переменных
 ,
, 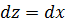 ,
,  ,
,
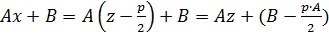 .
.
Имеем:
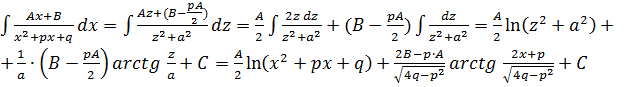 .
.
3. Пусть 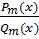 правильная дробь, т.е. m < n. Рассмотрим упрощенный вариант разложения многочлена на множители (полные способы разложения здесь не рассматриваются)
правильная дробь, т.е. m < n. Рассмотрим упрощенный вариант разложения многочлена на множители (полные способы разложения здесь не рассматриваются)
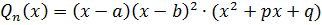 , т.е. n=5;
, т.е. n=5;
Тогда
 .
.
Найдя коэффициенты А,В,С и D, мы придем к вычислению трех уже известных интегралов
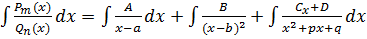 .
.
Пример 11
 .
.
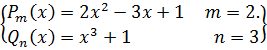 -> m < n дробь правильная.
-> m < n дробь правильная.
 –> разложили как сумму кубов
–> разложили как сумму кубов
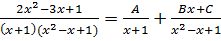 .
.
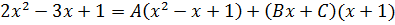 .
.
Т.к  имеет действительный корень х=-1 (х+1=0), то применим метод частных значений: подставим х=-1 в левую и правую часть разложения
имеет действительный корень х=-1 (х+1=0), то применим метод частных значений: подставим х=-1 в левую и правую часть разложения 
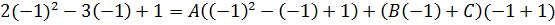 .
.
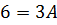 −> A=2.
−> A=2.
Других удобных значений X у нас нет. Применим метод сравнения коэффициентов при одинаковых степенях X в левой и правой частях.
 .
.
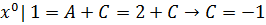 .
.
Имеем
 .
.
 .
.
Ø Необходимые сведения и формулы
Формулы сокращенного умножения
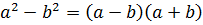 .
.
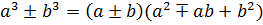 .
.
 .
.
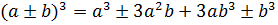 .
.
Поиск по сайту: