МЕТОД ШТРАФНЫХ ФУНКЦИЙ

Численные методы решения задач безусловной оптимизации и методы решения задач с ограничениями имеют качественное различие с точки зрения их трудоемкости (даже в случаях, когда множество допустимых решений имеет достаточно простую структуру, что позволяет использовать, например, метод проекций градиента или метод условного градиента). К трудностям отыскания безусловного минимума в методе условного градиентного спуска добавляются, например, решения задачи линейного программирования, причем эта задача решается на каждой итерации. В случае же нелинейных ограничений общего вида проблема еще более усложняется, и предложить какие-либо универсальные подходы сложно.

Одним из возможных подходов является метод штрафных функций. Он основывается на учете ограничений путем преобразования целевой функции исходной задачи оптимизации. При этом решение задачи с ограничениями получается как предел последовательности решений вспомогательных задач безусловной оптимизации. Эти методы выгодно отличаются от методов спуска для задач условной оптимизации простой реализацией и сильными свойствами сходимости.

К методу штрафных функций относится группа методов, связанных с параметризацией исходной задачи со смешанными ограничениями

Метод состоит в том, что задача (1.1-1.3) заменяется задачей безусловной оптимизации:

	,	(1.4)
	,	(1.5)

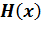где – коэффициент, а – функция, определяемая на основании ограничений (1.2-1.3) и называемая штрафной функцией.

В качестве штрафной функции может быть использована любая функция, обладающая свойствами:

1) Значения функции в допустимой области равны нулю

,

(1.6)

2) Значения функции вне допустимой области больше нуля

,

(1.7)

Теорема 1.1.Пусть 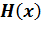– непрерывная функция, для которой выполняются условия (1.6-1.7). Если выполняются одно из двух условий:

1) ,

2) , D – ограниченна,

тогда при решение задачи (1.5) будет стремиться к решению задачи (1.1-1.3) и .

Для задач с ограничениями вида (1.2) используют следующие штрафные функции:

,

.

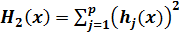Для задач с ограничениями вида (1.3) используют функции:

,

.

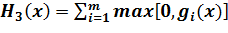Если задача со смешанными ограничениями, то используют функцию

.

Как видно из примеров, штрафные функции можно выбирать различными способами. При необходимости их можно подобрать так, чтобы они имели разные полезные свойства, такие, как, например, непрерывность, гладкость, выпуклость, простота вычислений значений функции и производных и так далее.

Чем больше штрафной коэффициент 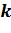, тем точнее решение задачи.

С другой стороны, при больших значениях 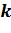задача становится плохо обусловленной, и численный метод решения может расходиться. Поэтому обычно задачу (1.5) решают неоднократно с различными коэффициентами 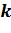, постепенно их увеличивая. При этом за начальное приближение каждой следующей задачи берётся точное решение предыдущей.

Алгоритм метода

Шаг 1. Задать начальную точку ; начальное значение параметра штрафа ; число для увеличения параметра; малое число для остановки алгоритма. Положить .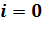

Шаг 2. Составить вспомогательную функцию

.

Шаг 3. Найти точку безусловного минимума функции 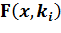по с помощью какого-либо метода безусловной оптимизации (например, метода Ньютона или метода градиентного спуска):

При этом задать все требуемые этим методом параметры. В качестве начальной точки взять . Вычислить .

Шаг 4. Проверить условие окончания поиска:

а) если , процесс поиска закончить:

, ;

б) если , положить: 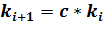, , и перейти к шагу 2.

Достоинства метода:

- сведение задачи к задаче безусловной оптимизации;

- метод может использоваться для задач смешанного типа;

- задача безусловной оптимизации решается в том же пространстве что и исходная: функция (1.5) не является существенно сложнее функции (1.1-1.3).

Недостатки метода:

- задачу (1.5) необходимо решать многократно при разных штрафных коэффициентах;

- если решение исходной задачи (1.1-1.3) находится на границе допустимой области, то решением задачи (1.5) всегда будет точка, не принадлежащая области допустимых решений задачи (1.1-1.3).

Пример

Задана функция с ограничением . Выполнить один шаг методом штрафных функций.

Решение

1.В качестве начальной точки возьмём , в качестве начального значения параметра штрафа и коэффициента его увеличения – 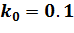и соответственно, ,

2.Построим новую целевую функцию. Для этого введём в неё функцию штрафа:

;

.

Целевая функция с учётом штрафа за нарушение ограничений:

.

3. Найдём точку с помощью метода Ньютона.

Алгоритм решения задачи безусловной минимизации методом Ньютона заключается в следующем.

1)Задаются , ; вычисляются , , ; полагается .

2) Вычисляется .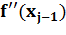

3) Определяется .

4) Вычисляются , , , .

5) Проверяется условие окончания вычислений .

Если оно выполняется, то полагается , и вычисления завершаются.

Если условие не выполняется,то полагается 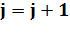и осуществляется переход к пункту 2.

В точке начальная функция цели равна нулю, а ограничение не удовлетворяется. Следовательно, на первом шаге метода штрафов функция .

Находим

; ;

;

; ; ;

.

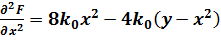Первая итерация метода Ньютона:

;

;

.

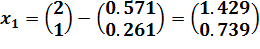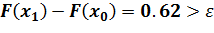Вторая итерация метода Ньютона:

;

;

;

.

.

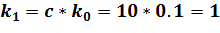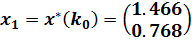4. Т. к. критерий остановки не выполняется, , то , , и переходим к шагу 2. Продолжаем вычисления до тех пор, пока не достигнем заданной точности.

Поиск по сайту: