 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Формула (2) является аналитическим выражением принципа Гюйгенса - Френеля
Смысл принципа Гюйгенса – Френеля заключается в том, что при вычислении интенсивности света в точке наблюдения реальный источник световой волны можно заменить совокупностью вторичных, расположенных вдоль волновой поверхности.
27.3. Метод зон Френеля
В связи с тем, что вычисления по формуле (2) часто оказываются весьма сложными, Френель разработал метод, позволяющий в симметричных случаях находить амплитуду результирующего колебания простым алгебраическим или геометрическим сложением.
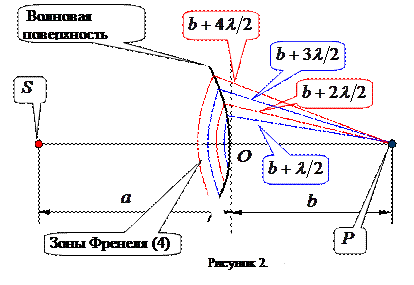Рассмотрим метод зон Френеля на примере волны, распространяющейся от точечного источника в однородной среде. Волна будет сферической, и волновые поверхности - сферы. Допустим, что по линии, соединяющей источник 
и точку наблюдения 
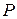, волновая поверхность, находится на расстоянии 
от источника и 
от точки наблюдения. Разобьем мысленно волновую поверхность на участки в виде кольцевых зон таким образом, чтобы расстояния от границ участков до точки наблюдения отличались на 
. Тогда расстояние 
от внешнего края m -ой зоны до точки 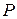будут определяться соотношением:
.
Построенные таким образом участки волновой поверхности называются ЗОНАМИ ФРЕНЕЛЯ.
Важнейшее свойство зон Френеля заключается в том, что колебания, создаваемые волнами, пришедшими от любых двух соседних зон в точку наблюдения, совершаются в противофазе, т.е. векторы электрического поля (светового вектора) оказываются в каждый момент времени противоположно направленными. Это следует из того, что для каждой точки в одной зоне обязательно найдется точка в другой зоне, расстояние от которой до точки наблюдения отличается на . Все точки волновой поверхности совершают колебания в одной фазе. Поэтому колебания от этих двух точек будут сдвинуты во времени на половину периода, поскольку расстояние в половину длины волны она проходит за половину периода. Соответственно суммарное колебание от всех точек одной зоны сдвинуто по фазе относительно результирующего колебания от точек соседней зоны на 
.
Отметим, что колебания, создаваемые точками, расположенными на краях данной зоны также совершаются в противофазе.
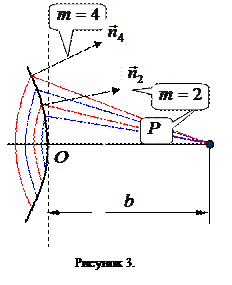Расчеты показывают, что при не очень больших номерах зон Френеля площади зон примерно одинаковы. Это позволяет утверждать, что амплитуды колебаний от соседних зон примерно одинаковы. Однако с увеличением номера зоны происходит, хотя и очень небольшое, увеличение расстояния до точки наблюдения, и возрастает угол 
, образованный нормалью к поверхности зоны и направлением в точку наблюдения. Плавно изменяющийся множитель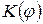 
уменьшается. Влияние этих двух факторов приводит к тому, что последовательность амплитуд колебаний от зон Френеля образует монотонно убывающую последовательность:
(3)
При этом можно утверждать, что между амплитудами трех любых ближайших зон имеется соотношение:
. (4)
Учитывая фазы колебаний, для результирующего колебания от всех зон можно написать следующее выражение:
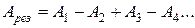(5)
Представим знакопеременную сумму (5) в виде:
(6)
Легко видеть, что, в силу соотношения (4), каждая из скобок в (6) равна нулю, а
(6)
Таким образом, полностью открытая волновая поверхность создает в точке наблюдения колебание с амплитудой, равной половине амплитуды, создаваемой первой зоной Френеля… Следовательно, закрыв все зоны, кроме первой, можно создать в точке наблюдения колебание с амплитудой в два раза большей, чем от источника света непосредственно. Отметим, что интенсивность света, пропорциональная квадрату амплитуды, увеличится при этом в 4 раза!
27.4. Метод графического сложения амплитуд
27.5. Метод графического сложения амплитуд
Напомним, что каждое колебание по методу векторных диаграмм можно представить вектором с длиной, пропорциональной амплитуде колебания, образующим с некоторым исходным направлением угол, равный начальной фазе колебания. Разобьём поверхность первой зоны Френеля (рисунок 4) на очень узкие подзоны такие, что амплитуды колебаний, создаваемых каждой из подзон можно было бы считать одинаковыми, а начальные фазы отличающимися на очень небольшой угол 
. Колебание, создаваемое каждой из подзон можно изобразить небольшим вектором.
Примем за начало отсчета вектор колебания от центральной подзоны(рисунок 4). Тогда векторы от последующих подзон будут составлять угол с вектором от предыдущей подзоны. Вектор колебания, создаваемого первой зоной Френеля, я получаются геометрическим суммированием векторов колебаний от от подзон и показан на рисунке 5. Если ширину подзон уменьшить, то отдельные векторы сливаются в сплошную полуокружность. Для каждой из зон Френеля вектор суммарный вектор колебания получается соединением начала и окончания соответствующей 
полуокружности. На рисунке 6 показаны векторы, соответствующие колебаниям от первой зоны Френеля и второй зоны Френеля. В силу плавного уменьшения амплитуды колебаний от зон Френеля с ростом их номера, каждая из последующих полуокружностей имеет меньший диаметр. Последовательность векторов амплитуд от подзон оказывается спиралью. Поэтому результирующее колебание от полностью открытой волновой поверхности изображается вектором, идущим от начала вектора для первой подзоны в центр спирали (рисунок 6.). Отметим, что модуль вектора колебания от всей волновой поверхности приблизительно равен модулю 
вектора колебаний от трети первой зоны Френеля. Поэтому можно считать, что в точку наблюдения вся энергия распространяется по узкому каналу с площадью сечения порядка трети первой зоны Френеля. Для оценки реальных размеоров зон укажем следующее: при 
и длины волны 0,5 мк радиус первой зоны Френеля составляет 0,5 мм.
В каждом конкретном случае можно изготовить зонную пластинку, которая закрывает, например, четные зоны Френеля и прозрачна для нечетных. Действие такой пластики будет напоминать собирающую линзу, в фокусе которой находится точка наблюдения. Действительно, амплитуда результиру-ющего колебания в точке наблюдения оказывается (рисунок 7) во много раз больше по сравнению с амплитудой от всей волновой поверхности.
Фазовая зонная пластика позволяет увеличить амплитуду еще в два раза. В отличие от зонной пластинки фазовая не закрывает четные зоны, а изменяет их фазу на . Этого можно достичь дополни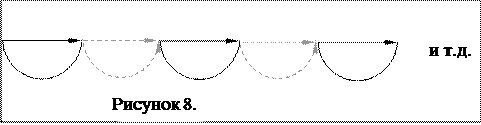 
тельным увеличением оптической длины пу-ти лучей, идущих от четных зон. Например, на пути этих лучей можно расположить прозрачные кольцевые пластинки соответствующей толщины.
Отметим, что плавно увеличивая толщину прозрачной пластики от краев к середине, можно компенсировать сдвиг фаз от каждой из подзон. В этом случае в точке наблюдения будет максимальная интенсивность, а фазовая зонная пластика превратится в линзу.
27.6. Дифракция от круглого отверстия
Представим, что на пути света от точечного источника к точке наблюдения 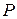установлена диафрагма с круглым отверстием изменяющегося радиуса. Пи увеличении радиуса отверстия диафрагмы от нуля интенсивность в точке 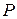сначала монотонно увеличивается до тех пор, пока диафрагма открывает площадь первой зоны Френеля. С момента, когда диафрагма начинает открывать площадь второй зоны, интенсивность в точке 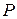начинает уменьшаться и уходит к очень малому значению при полном открытии второй зоны. Затем, при открывании третьей, интенсивность возрастает почти до максимального значения. Колебания от волн от четвертой зоны гасят колебания от третьей и т.д. Таким образом, при увеличении отверстия диафрагмы интенсивность света в точке наблюдения периодически изменяется.
Допустим теперь, что диафрагма установлена в положение, когда она открывает три зоны Френеля. Построим зоны Френеля для точки 
. Очевидно, что для этой точки преграда скрывает часть третей зоны (вверху) и открывает часть четвертой (внизу). Интенсивность света в этой точке будет меньше, чем в 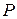, поскольку уменьшилась площадь видимой части третьей зоны, а открывшийся участок четвертой создает колебания противофазные колебаниям от третей зоны. Следовательно, при трех открытых зонах для точки 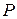при смещении по экрану от этой точки интенсивность света уменьшается. Если площади частей третьей и четвертой зоны для некоторой точки 
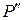окажутся равными, то интенсивность света в ней окажется равной нулю. При дальнейшем смещении откроется часть пятой зоны (создающей колебания, сдвинутые по фазе на 
относительно третьей) и скроется часть второй зоны. Интенсивность света начнет возрастать, поскольку будет возрастать суммарная площадь открытых частей нечетных зон. Далее ситуация будет повторяться. Таким образом, распределение интенсивности света на экране в окрестности точки наблюдения будет иметь вид, приблизительно показанный на рисунке 10.
 |
Если диафрагма оставляет открытыми четное число зон Френеля, то распределение интенсивности света на экране будет описываться графиком, представленным на рисунке 12. В центре дифракционной картины будет темное пятно, окруженное светлым кольцом.
При изменении отверстия диафрагмы происходит плавный переход от одного распределения к другому.
27.7. 
Дифракция от круглого диска
Допустим, что непрозрачный диск закрывает 
первых зон Френеля, и число невелико. Это означает, что на векторной диагармме, показанной на рисунке 6, отсутствуют первые полуокружностей. Поэтому результирующая амплитуда для центральной точки изменится незначительно. Поэтому в центре дифракционной картины должно быть светлое пятно.
Аналитически эта ситуация описывается следующим образом. Амплитуда результирующего колебания в центре дифракционной картины описывается выражением
(8)
Каждая из скобок в (6) равна нулю, и 
Если 
не сильно отличается от 
, то интенсивность в центре экрана будет почти такая же как в отсутствие преграды.
При смещении из центра 
зона частично скрывается и открывается -я зона. Поэтому интенсивность света убывает. Дифракционная картина будет иметь вид темных и светлых колец, но в центре обязательно будет светлая точка.
Однако если диск перекрывает много зон Френеля, то темные и светлые кольца наблюдаются только в окрестности геометрической тени, а светлая точка в центре отсутствует, из-за того, что интенсивность намного меньше интенсивности от центральной зоны.
27.8. Дифракция прямолинейного края полуплоскости
Представим, что на полу-плоскость с прямолинейным кра-ем падает плоская световая волна, фронт которой параллелен полуплоскости. Дифракционная картина должна наблюдаться на экране, расположенном на расстоянии параллельно полуплоскости. Результат дифракции в некоторой точке 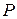экрана оценрим следующим обюразом. Разобьем волновую поверхность на зоны (это не есть зоны Френеля!) линиями, парллель-ными краю полуплоскости таким образом, чтобы расстояние от краев каждой зоны до точки наблюдения отличалось бы на небольшую величину 
. Это условие обеспечивает отличие колебаний, создаваемых каждой такой зоной, по сравнению с соседней по фазе на небольшой угол . Интенсивность колебаний в 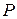определяется площадью зоны, ее расстоянием до точки 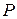и углом, под которым видна зона из точки наблюдения. Расчеты показывают (и это ясно из рисунка), что сначала, при небольших номерах зон, амплитуда колебаний с ростом номера зоны изменяется быстро, а потом медленнее. Поэтому векторная диаграмма для некоторого количества зон, находящихся справа от точки наблюдения будет иметь вид, показанный на рисунке 15. Для 
, стремящегося к нулю, получим кривую в виде спирали, сходящейся к некоторому фокусу 
(рисунок 16). Аналогично выглядит и спираль, построенная для точек, находящихся слева от точки наблюдения. Полученный рисунок называется спиралью Корню.
 |
Если точка наблюдения 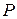находится непосредственно под границей полуплоскости, то амплитуда колебания будет изображаться вектором из точки О в (красным), поскольку все левые зоны закрыты.
Если рассматривать точки, находящиеся под полуплоскостью, то для них скрывается часть первых зон справа от 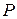. Поэтому начало результирующего вектора будет смещаться по спирали, и его модуль будет монотонно уменьшаться. Чем дальше вглубь геометрической тени, тем меньше амплитуда колебания.
Для точек, находящихся под открытой полуплоскостью открыты все правые зоны и часть левых. По мере их открытия начало результирующего вектора смещается по спирали, и он достигает максимального значения, показанного на рисунке 17 коричневым вектором. При дальнейшем удалении края полуплоскости результирующий вектор начинает уменьшаться, поскольку его начало будет приближаться к точке О. Поэтому по мере удаления от края полуплоскости амплитуда и интенсивность света будут осциллировать вблизи некоторого значения, но амплитуда осцилляций будет уменьшаться. Поэтому распределение интенсивности света по экрану будет примерно таким, как это показано на рисунке 18. Описанные изменения интенсивности света на экране действительно наблюдаются экспериментально, и на хорошо сделанных фотографиях вблизи края полуплоскости видны полосы с чередующейся интенсивностью.
.
27.9. Дифракция Френеля от щели – самостоятельно.
27.10. Дифракция Фраунгофера от щели
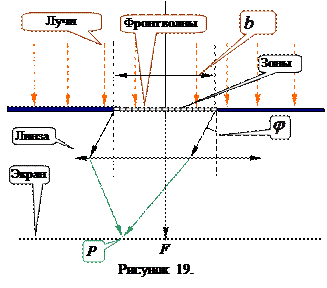
Представим себе, что на бесконечную щель шириной , образованную двумя полуплоскостями с параллельными краями падает плоская волна. Для наблюдения дифракции Фраунгофера расположим за щелью линзу, а в ее фокальной плоскости – экран. Линза собирает лучи, идущие под углом после дифракции на щели, в некоторой точке экрана Р.
Разобьем поверхность щели на очень узкие одинаковые зоны шириной 
с краями параллельными границам щели. Каждая зона создает в точке наблюдения колебание с амплитудой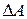 
. Фазы колебаний ососедних зон отличаются на небольшую величину , определяющуюся разностью хода от соответствующих точек соседних щелей, равной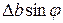 
.
Рассмотрим лучи, идущие за щелью под углом 
. Эти лучи соберутся линзой в точке в точке 
- фокусе линзы. Для таких лучей векторы колебаний от зон синфазны, и при сложении дадут некоторую амплитуду колебания 
.
Рассмотрим последовательно ситуации для лучей под различными углами , предполагая, что этот угол плавно увеличивается. Лучи идущие под маленьким после сложения дадут результирующий вектор 
. Точки с соответствующими интенсивностями света будут расположены симметрично относительно .
Если угол будет удовлетворять условию 
, то векторы от крайних зон окажутся в противофазе. В результате сум-мирования векторов получим амплитуду 
.
Если угол будет удовлетворять условию 
, то векторы от крайних зон окажутся в сдвинутыми на . Амплитуда колебаний в соответствующей точке (и симметричной ей) оказывается равной нулю: 
.
Однако при дальнейшем увеличении , для условия 
, При той же суммарной длине векторов, амплитуда достигнет результирующего значения 
. Следовательно, на экране симметрично фокусу будут две точки, в которых интенсивность света достигает максимального значения, однако по сравнению с центральным максимумом интенсивность в них будет намного меньше.
Поиск по сайту: