Функция

Рассмотрим некоторое отображение f: X®Y. Как уже говорилось, это отображение называется функцией, если оно однозначно, т.е. если для любых пар (х₁, у₁₎Îf и (х₂, у₂)Îf из х₁=х₂ следует у₁=у₂.

Y

y₁

y₂

X

x₂ x₁

Рис. 1.10

Однозначное соответствие, определенное формулой f: X®Y называют функцией с вещественными значениями, если YÍR.1

Пример. Из пункта А в пункт В передача единицы сообщения по телефону, телеграфу, телемонитору, телефаксу стоит соответственно a, b, c, d. Тогда стоимость передачи сообщения можно представить как функцию от вида передачи. Для этого рассмотрим множества:

Х={телефон, телеграф, телефакс, телемонитор};

Y={a, b, c, d}.

Функция f: X®Y, получаемая из условий, может быть записана в виде: f={(телефон, а); (телеграф, b); (телефакс, с); (телемонитор, d)}.

Значение у в любой из пар (х, у)Îf называют функцией от данного х и записывают в виде: у=f(x). Такая запись позволяет ввести следующее формальное определение:

f={(x, y)ÎX´Y | y=f(x)} 1.45

Таким образом, символ f используют при определении функции в двух смыслах:

· f является множеством, элементами которого будут пары (х, у), участвующие в соответствии;

· f(x) является обозначением для yÎY, соответствующего данному хÎХ.

Функция типа А₁´А₂´….´А_n ® В называется n – местной функцией. В этом случае принято считать, что функция имеет n аргументов: f(a₁,a₂,…a_n)=b, где a₁ÎA₁, a₂ÎA₂, … a_nÎA_n, bÎB.

Пусть даны функции f:A®B и g:B®C. Функция h:A®C называется композицией функций f и g, если имеет место равенство: h(x) = g(f(x)), где хÎА. Композиция функций обозначается f◦g. Композиция функций f и g представляет собой последовательное применение этих функций-g применяется к результату f, т.е. функция h получается подстановкой f в g. Для многоместных функция f:Aⁿ®B и g:A^m®C возможны различные варианты подстановок f в g, дающие функции различных типов. Особый интерес представляет случай, когда задано множество функций типа: f₁: f_m: 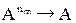. В этом случае возможны, во-первых, любые подстановки функций друг в друга, а во-вторых, любые переименования аргументов. Функция, полученная из данных функций f₁, f₂, … f_m некоторой подстановкой их друг в друга и переименованием аргументов, называется их суперпозицией.

Поиск по сайту: