Частинні похідні вищих порядків

Нехай функція задана в деякій відкритій області і в усіх точках цієї області має частинні похідні . Ці похідні називають частинними похідними першого порядку.

Частинні похідні першого порядку, будучи функціями від х та у, в свою чергу, в якійсь точці можуть мати частинні похідні.

Означення 4.1. Нехай функції мають в точці частинні похідні. Ці частинні похідні називають частинними похідними другого порядку від функції і позначають , , , 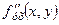або , , , .

При цьому називають частинною похідною другого порядку по х ²; - частинною похідною другого порядку по ху; 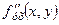- частинною похідною другого порядку по ух; - частинною похідною другого порядку по у ².

Отже, згідно означення, маємо:

, ,

, .

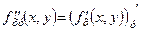Таким чином, для знаходження частинних похідних другого порядку потрібно спочатку знайти частинні похідні першого порядку даної функції, а потім від них знайти відповідні частинні похідні першого порядку. Аналогічно, шукаючи частинні похідні першого порядку від частинних похідних другого порядку, знаходимо тим самим частинні похідні третього порядку.

Індуктивно можна означити частинні похідні п -го порядку як частинні похідні першого порядку від частинних похідних (п - 1)-го порядку. Частинні похідні п -го порядку позначають так:

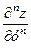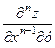, , , і т. д.

Приклад 4.1. Знайти частинні похідні другого порядку для функції .

Р о з в′ я з а н н я

Знайдемо спочатку частинні похідні першого порядку:

, .

Тоді

,

,

,

.

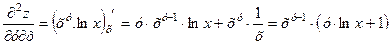Зауваження 4.1. Ми бачимо, що для розглянутої в останньому прикладі функції частинні похідні та , які називаються мішаними частинними похідними другого порядку, рівні між собою. Постає природнє запитання: чи завжди ? Виявляється, що це не завжди так.

Приклад 4.2. Розглянемо функцію

Покажемо, що для цієї функції в точці О (0;0) існують обидві мішані частинні похідні другого порядку та знайдемо їх.

Легко бачити, що частинні прирости в точці О (0;0) дорівнюють:

;

.

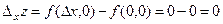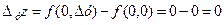Тому існують

,

.

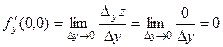Якщо ж 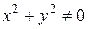, тобто , то, використовуючи правила диференціювання, матимемо:

. (4.2)

Поклавши в рівності (4.1), отримаємо . Тоді, згідно означення частинної похідної, знаходимо

.

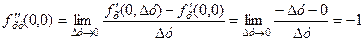При з рівності (4.2) маємо , звідки

.

Отже, для розглядуваної функції

.

Якщо ж на функцію накласти деякі додаткові умови, то на поставлене в зауваженні 4.1 можна отримати ствердну відповідь.

Теорема 4.1. Нехай функція визначена і має частинні похідні , в області , якій належить точка разом зі своїм деяким околом, причому похідні є неперервними функціями в точці 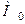. Тоді має місце рівність

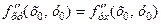. (4.3)

Д о в е д е н н я. Виберемо в області D якийсь окіл точки 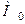і візьмемо в ньому довільну точку , таку щоб . Побудуємо вираз

. (4.4)

Розглянемо функцію

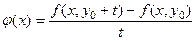, (4.5)

в область визначення якої, очевидно, входить відрізок (або відрізок 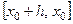, якщо ). Згідно умов теореми функція в усіх точках цього відрізка має похідну

, (4.6)

а отже, й неперервна на відрізку . Таким чином, на вказаному відрізку для виконуються всі умови теореми Лагранжа, відповідно до якої існує таке число , що виконується рівність

(4.5)

Легко бачити, що за допомогою функції (4.5) вираз (4.4) можна записати так:

.

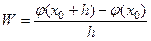Тоді з рівності (4.5) з врахуванням (4.6) отримуємо

. (4.6)

Розглянувши далі функцію 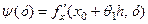, яка в усіх точках відрізка (або відрізка , якщо ) має похідну 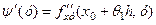, тому, застосувавши теорему Лагранжа, матимемо

, (4.7)

де .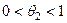

Розглядаючи функцію

,

аналогічно до (4.6) отримуємо

,

де ,

звідки, аналогічно до (4.7), дістанемо

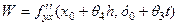, де 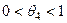. (4.8)

Тоді з рівностей (4.7) та (4.8) маємо

. (4.9)

Очевидно, що

при ;

при .

Тому, переходячи в рівності (4.9) до границі при , і враховуючи неперервність частинних похідних в точці , отримуємо рівність (4.3), чим і доводимо нашу теорему.

Зауваження 4.2. Щойно доведена теорема узагальнюється на випадок мішаних похідних третього і більш вищих порядків.

Поиск по сайту: