Формула Тейлора для функції двох змінних

В теорії функцій однієї дійсної змінної важливу роль відіграє формула Тейлора. Не менш важливе значення має вона і для функцій декількох змінних. Ми виведемо формулу Тейлора, розглядаючи для спрощення викладок функцію двох змінних.

Нехай функція визначена і має неперервні частинні похідні до (п +1)–го порядку включно в деякому околі точки . Візьмемо в цьому околі якусь точку і сполучимо її з точкою 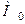відрізком прямої лінії. Рівняння цієї прямої як прямої, що проходить через дві точки 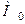та М, буде таким: . Звідси,

. (4.16)

Якщо в рівностях (4.16) взяти t = 0, то дістанемо координати точки 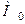, а якщо t = 1, то координати точки М. Тому можемо вважати, що t змінюється на відрізку , тобто .

Функція вздовж відрізка змінюватиметься як функція однієї змінної t на відрізку :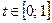

. (4.17)

Згідно припущення функція визначена і має неперервні частинні похідні до (п +1)–го порядку включно в околі точки , якому належить відрізок . Тому складена функція 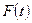має на відрізку неперервні похідні до (п +1)–го порядку включно. Значить, для функції 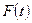можна записати формулу Маклорена п –го порядку з залишковим членом в формі Лагранжа:

де .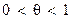

Поклавши тут t = 1, з врахуванням (4.17) дістанемо:

. (4.18)

Знайдемо тепер і т. д., .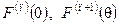

Диференціюючи (4.17) та враховуючи рівність (2.20) в теоремі 2.4, матимемо

Беручи до уваги (4.16), останню рівність запишемо так:

.

Тепер знаходимо , пам¢ятаючи, що 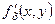та є складеними функціями (х і у залежать від t за формулами (4.16)), а 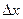і 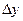- сталі числа:

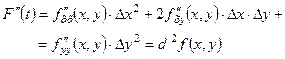
Аналогічно знаходимо

,

і т. д.,

.

Поклавши t = 0 в отриманих формулах для і для 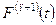, з врахуванням (4.16) матимемо:

, .

Тоді формулу (4.18) можна записати так:

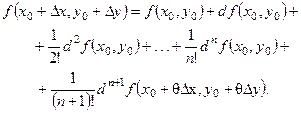(4.19)

Формула (4.19) називається формулою Тейлора п –го порядку для функції двох змінних з залишковим членом в формі Лагранжа в околі точки .

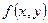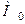Зауваження 4.5. Відзначимо, що якщо умови, накладені на функцію , послабити, а саме, вимагати, щоб вона мала неперервні частинні похідні до (п -1)–го порядку включно в деякому околі точки , а в самій точці була диференційованою до п –го порядку, то тоді функцію 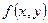можна розвинути за формулою Тейлора п –го порядку залишковим членом в формі Пеано:

(4.20)

де - нескінченно мала функція при .

Як бачимо, формула Тейлора у вигляді (4.19) чи (4.20) зовні нічим не відрізняється від формули Тейлора для функції однієї змінної, записаної в диференціальній формі. Проте в розгорнутому вигляді для функції двох змінних вона буде значно складніша. Запишемо, наприклад, формулу (4.20) для випадку п =2, позначивши , тобто :

Зауваження 4.6. Для функції трьох і більшої кількості змінних також можна записати формулу Тейлора при відповідних умовах на функцію. Так, наприклад, якщо функція 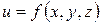визначена і має неперервні частинні похідні до (п +1)–го порядку включно в деякому околі точки , то, аналогічно до (4.19), можна записати:

Приклад 4.6. Розвинути за формулою Тейлора другого порядку функцію в околі точки

Р о з в′ я з а н н я

Задана функція має неперервні частинні похідні будь-якого порядку в усіх точках площини. Знайдемо усі частинні похідні до другого порядку включно та обчислимо їхні значення, а також значення функції в заданій точці .

;

, ;

, ;

, ;

, ;

, .

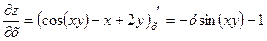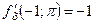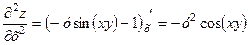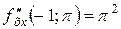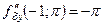Тоді, підставивши та обчислені значення частинних похідних в заданій точці, матимемо:

Лекція 5 Екстремуми функцій декількох змінних

Поиск по сайту: