 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Чувствительность систем автоматического управления
Чувствительность систем автоматического управления - это степень влияния разброса параметров и их изменений в процессе работы на статические и динамические свойства системы управления, то есть на точность, показатели качества, на частотные свойства и др.
Параметры системы управления (коэффициенты передачи и постоянные времени) определяются физическими параметрами составляющих ее элементов (резисторов, конденсаторов, катушек индуктивностей и т.п.). Величины физических параметров элементов, во-первых, имеют технологический разброс, обусловленный допусками на изготовление элементов, во-вторых, подвержены эксплуатационным изменениям с течением времени, что обусловлено их старением.
Поэтому встает задача оценки работы системы при изменении и разбросе параметров составляющих ее элементов.
Эта задача решается путем количественной оценки чувствительности системы.
Для этого требуется описать систему управления уравнениями в нормальной форме
 , при i = 1, 2, …, n , при i = 1, 2, …, n
| (10.14) |
где n - порядок системы; xi - координаты состояния системы; fi - внешние воздействия, прикладываемое к системе; aik - коэффициенты уравнения, определяемые величинами физических параметров составляющих систему элементов.
Изменяющиеся со временем параметры элементов системы в процессе эксплуатации и от разброса при изготовлении обозначим через αj (j=1, 2,..., m). Тогда уравнение системы (10.14) можно записать в виде
 , при i = 1, 2, …, n , при i = 1, 2, …, n
| (10.15) |
Решение уравнений (7.15) определяет координаты системы: x1(t), x2(t),..., xn(t), образующие исходное движение системы.
Пусть параметры αj изменяются на малые величины Δαj, тогда имеем
 ;
……………….. ;
………………..
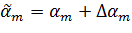
|
Рассматривая малые изменения параметров αj (j=1, 2,..., m), получим новые уравнения
 , при i = 1, 2, …, n , при i = 1, 2, …, n
| (10.16) |
Процесс в той же системе, но с измененными параметрами, определяемый решением уравнений (7.16), называется варьированным движением.
Возникшее различие в протекании процессов в системе за счет изменения параметров
 , при i = 1, 2, …, n , при i = 1, 2, …, n
|
называется дополнительным движением.
При малых отклонениях Δαj эта разность может быть определена следующим образом:
 , при i=1, 2,..., n. , при i=1, 2,..., n.
| (10.17) |
Обозначим
 , при j=1, 2,..., n. , при j=1, 2,..., n.
| (10.18) |
Тогда дополнительное движение будет
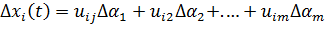 , при i=1, 2,..., n. , при i=1, 2,..., n.
| (10.19) |
Величины uij(t), определяемые выражением (10.18), представляют собой функции чувствительности i-ой координаты системы по j-ому параметру.
Таким образом, чтобы оценить степень влияния разброса и изменения параметров на координаты системы необходимо определить функции чувствительности по каждой координате от каждого изменяющегося параметра.
В рассматриваемом случае xi(t) являются координатами состояния системы. Вообще же аналогичные характеристики чувствительности вводятся так же для различных показателей качества системы. Тогда в формуле (10.18) вместо xi будет стоять соответствующий показатель качества, а в формуле (10.19) - вместо Δxi - изменение этого показателя качества. Функции чувствительности для частотных характеристик будут функциями не времени, а частоты. Если показатели качества выражаются не функциями, а числами, то uij называются коэффициентами чувствительности.
Если в качестве изменяющихся параметров αj выбрать внешние воздействия, то можно получить функции чувствительности системы по отношению к внешним воздействиям.
Определение функций чувствительности производится следующим образом.
Продифференцируем исходное уравнение (10.15) по изменяющимся параметрам αj. Меняя в левой части порядок дифференцирования и учитывая (10.18), получим выражения, которые называются уравнениями чувствительности. Решение этих уравнений определяет функции чувствительности uij(t).
Контрольные вопросы
1. Перечислите общие методы повышения точности систем управления. Поясните их.
2. Дайте понятие астатических системы управления. Каким образом определяется степень астатизма?
3. В чем преимущество повышения степени астатизма системы с помощью изодромных устройств?
4. Какая система является инвариантной по отношению к внешним воздействиям?
5. Что понимается под комбинированным управлением?
6. Как определяются передаточные функции компенсирующих устройств в комбинированных системах?
7. Для каких целей используются неединичные главные обратные связи?
8. Сформулируйте понятие чувствительности систем управления.
9. Каким образом можно получить уравнения чувствительности?
10. Что представляют собой функции чувствительности и коэффициенты чувствительности?
Лекция 11. Показатели качества. Критерии качества переходного процесса. Понятие коррекции. Способы коррекции САУ: последовательная коррекция динамических свойств, параллельная коррекция.
План лекции
1. Показатели качества
2. Критерии качества переходного процесса
3. Способы коррекции САУ
4. Контрольные вопросы
Поиск по сайту: