АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Тіла обертання. Об’єми та площі поверхонь геометричних тіл

Читайте также:
  1. Визначення площі листка ваговим методом
  2. Визначення розмірів та площі зони хімічного забруднення
  3. Додавання поверхонь
  4. Допуски та відхилення форми поверхонь
  5. Лекція № 11. Взаємний перетин геометричних поверхонь
  6. Методика навчання учнів розв’язувати задачі на обчислення периметра та площі геометричних фігур.
  7. Многогранники. Об’єми та площі поверхонь геометричних тіл
  8. Об’ємів тіл обертання.
  9. Основні методи геометричних побудов (метод ГМТ, методи осьової та центральної симетрії, метод паралельного перенесення, метод гомотетії, алгебраїчний метод).
  10. Підготовка поверхонь
  11. Поняття площі плоскої фігури, її основні властивості та способи вимірювання. Рівновеликі та рівноскладені фігури. Одиниці вимірювання площі та співвідношення між ними.
  12. Розрахунок ємності й площі складів

1. Прямокутник зі сторонами 5см та 9см обертається навколо меншої сторони. Знайти площу осьового перерізу отриманого циліндра.

2. Осьовий переріз циліндра – квадрат, площа якого дорівнює 100 см2 . Знайдіть площу основи циліндра.

3. Осьовий переріз циліндра – квадрат, периметр якого дорівнює 16 см . Знайдіть площу основи циліндра.

4. Відрізок, який з’єднує центр верхньої основи циліндра з точкою кола нижньої основи, дорівнює 6 см та утворює з площиною нижньої основи кут 45 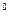. Знайти об’єм циліндра.

5. Діагональ осьового перерізу циліндра дорівнює 12 см, та утворює з площиною нижньої основи кут 45 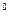. Знайти об’єм циліндра.

6. Площа осьового перерізу циліндра дорівнює 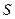, а діагональ перерізу утворює ї площиною основи кут . Знайти об’єм циліндра.

7. Площа осьового переріза циліндра дорівнює 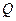, а відрізок, який з’єднує центр верхньої основи циліндра з точкою кола нижньої основи, утворює ї площиною основи кут . Знайти об’єм циліндра.

8. Радіус основи циліндра 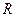, висота . Знайдіть кут нахилу діагоналі осьового перерізу до площини основи.

9. Радіус основи циліндра 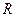, діагональ осьового перерізу 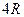. Знайдіть кут між твірною та діагоналлю перерізу.

10. Довжина кола основи конуса дорівнює см, а його висота – 3 см. Знайдіть твірну конуса.

11. Площа основи конуса дорівнює 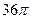см2, а його твірна - 10 см. Знайдіть висоту конуса.

12. Осьовий переріз конуса – правильний трикутник зі стороною 4 см. Знайти об’єм конуса.

13. Осьовий переріз конуса – рівнобедрений трикутник з кутом при вершині 120 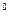та бічною стороною 6 см. Знайти об’єм конуса.

14. Радіус основи конусу дорівнює 5 см, а твірна – 11 см. Знайти висоту конуса.

15. Радіус основи конусу дорівнює 5 см, а твірна – 11 см. Знайти площу повної поверхні конуса.

16. Твірна зрізаного конуса дорівнює 5 см, а радіуси основ – 3 см і 6 см. Знайдіть площу осьового перерізу.

17. Радіуси основ зрізаного конуса дорівнюють 3 і 7 см, а твірна –5 см. Знайдіть площу осьового перерізу.

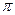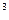18. Об’єм кулі дорівнює 36 см . Знайти діаметр кулі.

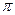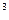19. Об’єм кулі дорівнює 288 см . Знайти діаметр кулі.

 


1 | 2 | 3 | 4 | 5 | 6 | 7 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.004 сек.)