Общая постановка задачи оптимального управления

Рассмотрим общую постановку задачи оптимизации экономических систем. Пусть имеется система, состояние которой может изме­ниться в результате некоторого количества управляющих воздействий. Задавая эти воздействия, можно получить определенный процесс изменения состояния си­стемы. При этом возникают две задачи: первая предполагает выбор таких воздействий на систему, чтобы проис­ходящий процесс удовлетворял заданным условиям, такие процессы принято называть допустимыми), вторая задача - выбор из этого множества допустимых процессов наилучшего (оптимального) процесса.

Чтобы решать оптимизационные задачи с помощью мате­матических методов, нужно сформулировать на математическом языке рассматриваемые процессы, ограничения, накладываемые на состояние системы и управляющие воздействия, а так же записать математические модели, описывающие эти процессы.

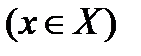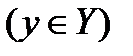Введем некоторые понятия и обозначения. Рассмотрим множество М с эле­ментами v , где v - пары вида v =(x, у), , , X,Y - некоторые заданные множества. Проек­цией множества М на множество Х назовем подмножество М_x, обладающее тем свойством, что для каждого существу­ет такой элемент , что пара 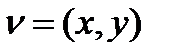содержится в мно­жестве М.

Введем понятие сечения М^x множества М при данном x. Сечением М^x будем называть множество всех y, при которых пара 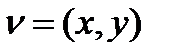принадлежит множеству М.

Введем понятие функционала, являющегося одним из главных в задачах оптимального управления. Будем говорить, что на мно­жестве М задан функционал F, если известно правило, которое каждому элементу ставит в соответствие определенное действительное число F (v).

В общем виде задача оптимизации формулируется как задача отыскания минимального (или максимального) значения функ­ционала F (v) на множестве М.

Предположим, что требуется минимизировать функционал F (v) на множестве М. Если решение этой задачи существует (обозначим его через ), то называется опти­мальным элементом множества M, а величина - оптимальным значением функционала. Решения поставленной задачи F и будем записывать следующим образом:

.

Аналогично формулируется задача о нахождении максималь­ного значения функционала.

Введем понятия точной нижней и верхней границы функцио­нала. Точной нижней границей функционала F (v) на множестве М назовем такое число т, если:

1) для любого ;

2) существует последовательность , на которой .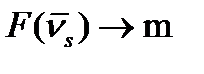

Точная нижняя граница функционала обозначается

.

Последовательность { v_s } называется минимизирующей.

Точно так же определяется точная верхняя граница n функ­ционала F (v):

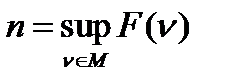
Назовем функционал F (v) ограниченным снизу (сверху) на множестве М, если существует такое число A, что при всех . Если функционал является ограниченным снизу (сверху), то решение задачи о нахождении его точной нижней (верхней) границы существует, т. е. имеет место следую­щая теорема (приведем без доказательства): Пусть на множестве М задан ограниченный снизу функционал F (v). Тогда реализуется одна из двух возможностей:

1) Существуют элемент и число , при которых при всех .

2) Существуют последовательность { v_s } элементов множе­ства М и число , удовлетворяющее условиям , 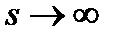и 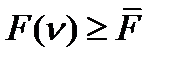при всех .

Данная теорема имеет важное значение для понимания сущности задачи оптимизации по двум причинам. Во-первых, она говорит о том, что постановка задачи об отыскании наименьшего (наибольшего) значения ограниченного снизу (сверху) функционала имеет смысл. Во-вторых, она объясняет природу решения такой задачи. А именно: решением будет либо определенный элемент множества М, минимизирующий (максимизирующий) функци­онал F (v), либо последовательность элементов множества М, являющаяся миними­зи­рующей (максимизирующей) последо­вательностью. В первом случае можно говорить о точном решении задачи, а во втором - о приближенном.

Задачи оптимизации управляемых процессов (оптимального управления) являются частными по отношению к сформулированной выше общей задаче оптимизации. Рассмотрим постанову задач оптимального управления.

Введем некоторые понятия.

Важнейшими из них являются понятия состояния системы и управления. Будем рассматривать системы, состояние которых может быть в любой момент времени определено вектором х n -мерного пространства с координатами 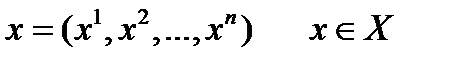. Пространст­во Х будем называть пространством состояний системы.

Так как система изменяется во времени, то ее поведение можно описать последовательностью состояний. Такую последовательность системы 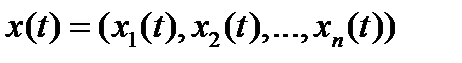называют ее траекторией.

Переменная t (называется аргу­ментом процесса) может быть некоторым отрезком числовой прямой или отрезком натурального ряда . В первом случае процесс, происходящий в системе, называется непрерывным, во втором случае - многошаговым, а системы - соот­ветственно непрерывными и дискретными.

Изменение состояния системы, т. е. процесс в ней, может происходить в результате управляющих воздействий. Будем рассматривать системы, управляющие воздействия в которых моделируются с помощью элементов r -мерного про­странства U:

, .

Управляющие воздействия могут задаваться в виде функций от t, т.е. .

На допустимые состояния системы x(t) и управ­ления u(t) могут быть наложены ограничения. Рассмотрим множество троек (t,x,u) - совокупность (n+r+1) - мерных векто­ров в пространстве R^n+r+1. Тогда ограничения на состояние системы и управление в самом общем случае могут быть записаны в виде

,

где - некоторая область (подмножество) рассматривае­мого (n+r+1) - мерного пространства. Ограничения на величины x(t), u(t) в каждый фиксированный момент времени t могут быть заданы и в виде

,

где V^t - сечение множества V при заданном значении t.

Пару функций назовем процессом. Между функ­циями x(t), u(t) имеется связь: как только задано управление u(t) системой, последовательность ее состояний (траектория системы) x(t) определяется однозначно. Связь между x(t) и u(t) моделируется по-разному в зависимости от того, является система непрерывной или дискретной.

Для непрерывных систем модели процессов задаются системой дифференциальных уравнений вида

,

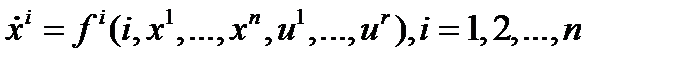или в векторной форме

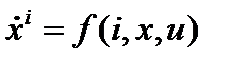. (2.1)

Пусть задано состояние, в котором система находилась в начальный момент t₀. Для простоты этот момент примем равным нулю, а момент окончания процесса t₁- равным Т. Тогда аргумент процесса t изменяется в пределах , а начальным состоянием системы будет вектор

, (2.2)

где - начальное значение i -й координаты вектора со­стояния системы.

Проанализируем, каким образом модель отражает связь между управлениями и состоянием системы, изменяющимся под их воздействием. Пусть на промежутке задано управление u(t). Подставляя его в правую часть системы (2.3), получим

(2.3)

Имеем систему дифференциальных уравнений относительно неиз­вестной функции . Решая ее с учетом начальных условий (2.2), получим x(t). Это решение и есть траектория, отвечающая заданному управлению u(t).

Модель дискретной управляемой системы имеет вид системы рекуррентных уравнений:

, .

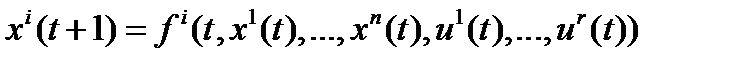В векторной форме эту модель можно записать в виде

, (2.4)

Здесь t принимает значение t=0,1,…,T-1. Начальное зна­чение x(0)=x₀ будем считать известным.

В дискретной системе, как и в непрерывной, задание управляющих воздействий u(t) при t=0,1,…,T-1 позволяет однозначно определить отвечающую им траекторию системы. При подстановке значения u(t) в правую часть (4.2.4) получаем систему уравнений, которая позволяет при известном значении состояния u(t) в момент времени t определить состояние x(t+1) в следующий момент времени. Так как в начальный момент t=0 состояние x(0)=x₀ известно, то, подставив его в правую часть (4.2.4), получим

.

Подставляя затем найденное значение x(1) и t=1 в (2.4), так же найдем значение x(2). Продолжая этот процесс, через Т шагов получим последнее искомое значение x(T).

Таким образом, и в дискретном случае уравнения модели (2.4) позволяют однозначно определить траекторию системы x(t), если задано управление u(t).

Следовательно, процесс должен удовлетворять следующим ограничениям:

1) при всех ;

2) Пара удовлетворяет системе уравнений процесса:

а) системе (2.1) в непрерывном случае при ;

б) системе (2.4) в дискретном случае при t=0,1,…,T-1;

3) Заданы начальные условия (2.2);

4) В непрерывном случае на функции x(t), u(t) накла­дываются некоторые дополнительные ограничения, связанные с применимостью употребляемых здесь математических записей. Функцию u(t) будем считать кусочно-непрерывной, а век­тор-функцию x(t) - непрерывной и кусочно-дифференцируемой.

Процессы , удовлетворяющие условиям 1) – 4), будем называть допустимыми. Таким образом, допустимый процесс - это управляющие воздействия u(t) и соответствующая им траектория системы x(t), удовлетворяющие перечисленным ограничениям.

Для постановки оптимизационной задачи необходимо ввести в рассмотрение функционал F, задан­ный на множестве М. Задача оптимального управления будет состоять в выборе элемента множества M, на котором функционал F достигает минимального значения. Такой процесс называют оптимальным процессом, управление - оптимальным управлением, а траекторию оптималь­ной траекторией.

Функционал F, заданный на множестве допустимых процессов, описывает цель, согласно которой оптимизируется процесс.

В задачах оптимального управления для непрерывных систем будем рассматривать функционалы следующего вида:

, (2.5)

где ; - задан­ные функции. Выражение (2.5) позволяет вычислить для каждого допустимого процесса определенное значение и тем самым задать функционал на множестве допустимых процессов. Для этого необходимо подставить x(t), u(t) вместо аргументов функции , которая становится функцией времени, после чего вычислить ее интеграл. Затем к значению интеграла прибавляем значение функции при .

Функционал состоит из двух частей: и 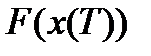. Первое из этих слагаемых оценивает качество процесса на на всем промежутке , второе слагаемое - качество конечного состояния системы. Иногда в за­дачах оптимального управления конечное состояние системы задается. В этом случае второе слагаемое функционала (4.2.5) есть величина постоянная и, следовательно, не влияет на его минимизацию. Такие задачи называются задачами с фик­сированным правым концом траектории.

Для задач оптимизации в дискретных системах функционал имеет вид

. (2.6)

К функционалу (2.6) относятся все замечания и комментарии, сделанные к функционалу (2.5).

Таким образом задача оптимизации управляемых процессов сводится к постановке задачи о ми­нимуме функционала (2.5) в непрерывном и (2.6) в дискретном случае на множестве М допустимых процессов , удовлетворяющих ограничениям 1)-4).

Эта задача может решаться в двух вариантах:

1. Определить оптимальный процесс , чтобы

;

2. Определить минимизирующую последовательность , чтобы

.

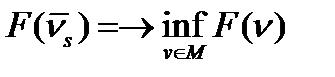В теории оптимального управления термины «состояние» и «управление» имеют содержательный смысл. Он заключается в том, что, задавая управление u(t), мы задаем и траекторию процесса x(t), а изменяя управляющие воздействия u(t) - «управляем» процессом.

Из условия можно выделить ограничения на состояние и управление:

, ,

Где - проекция множества на пространство X; - сечение множества при данном

В задачах оптимального управления область возможных состояний часто является постоянной или совпадает со всем пространством, а область возможных управлений не зависит от x. Эти предположения выполняются в большом числе практических случаев, что упрощает решение задачи.

Выше предполагалось, что про­межуток времени фиксирован, т. е. задан момент Т окон­чания процесса. Однако возможны постановки задач, где этот момент не задан, а определяется решением задачи. Это относится, в частности, к так называемым задачам о быстродействии, когда требуется перевести систему (2.4) из заданного начального состояния х(0)=х₀ в заданное конечное состояние , минимизируя при этом время T протекания процесса.

Поиск по сайту: