Эффект Эттингсгаузена

Эффект Эттингсгаузена в общем случае формулируется следующим образом: в направлении перпендикулярном к плотности тока j и магнитной индукции приложенного магнитного поля В возникает температурный градиент равный

где Э – коэффициент Эттингсгаузена.

Рассмотрим этот эффект подробнее. Перенос энергии электромагнитного поля происходит вдоль проводника и определяется нормальной составляющей электрического поля волны. В результате на поверхности 1 (см. рис. 163) общая перенесенная энергия за время ∆t составит:

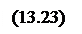
где l –длина проводника и S –площадь его сечения.

Вследствие поглощения этой энергии поверхностью 1 ее температура возрастет на величину ∆Т = Т₀ + Т₁ (Т₀ – начальная температура). Тогда поглощенная теплота может быть оценена иначе, а именно

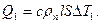
Для поверхности 2 соответственно имеем:

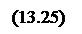
Разности этих двух величин на поверхностях 1 и 2 равны соответственно

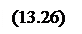
В соответствии с законом сохранения энергии и равенством Е_n = Е_τ получаем:

Поделим равенство (13.27) на d = ∆y и учтем равенство (13.4). После несложных преобразований получим:

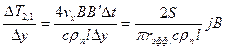
Сравнивая (13.28) с равенством (13.22), для коэффициента Эттингсгаузена получаем следующее выражение:

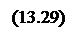
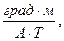
Для медного проводника в нормальных условиях Э_Cu = 2,74∙10^-7

а для алюминиевого проводника Э_Al = 3,92∙10^-7

Для проводников размером b · d · l = 1·10·10 мм при токе 10 А и внешнем магнитном поле В = 1 Т градиент температуры для медного образца составит 0,274 К/м и для алюминиевого образца 0,392 К/м. Такие незначительные градиенты температур вполне могут быть измерены.

Этот эффект был открыт Эттингсгаузеном и носит его имя.

Поиск по сайту: