Исследование устойчивости состояния равновесия нелинейной системы по первому приближению (второй метод Ляпунова)

В общем случае нелинейная система с N степенями свободы описывается нелинейными уравнениями 1-го порядка

, (6.41)

где – нелинейные функции своих аргументов.

Системы динамических уравнений (6.41) будем считать стандартной и дальнейшие рассуждения будут проводиться применительно к этой форме. Если динамические уравнения имеют другую форму, то путем замен и преобразований их можно привести к стандартной форме.

Состояние равновесия такой системы определится из обычного условия стационарности, когда производные равны нулю:

. (6.42)

Получаем систему нелинейных алгебраических уравнений

. (6.43)

Из системы уравнений (6.43) находим координаты, в которых система находится в состоянии равновесия;

. (6.44)

В общем случае число корней уравнения (6.43) может быть больше n, т.е. у системы существует несколько состояний равновесия. Какое их них реализуется – и является целью исследования устойчивости. Второй метод Ляпунова указывает, как проводить это исследование и, главное, формулирует условия (теоремы Ляпунова), которые гарантируют правильность полученных результатов.

Для исследования устойчивости состояния равновесия с координатами , нелинейной системе (6.41) сопоставляется некоторая возмущенная система. Для этого предполагается, что координаты х _i мало отличаются от равновесных

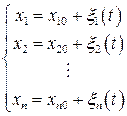, (6.45)

где все .

Ввиду малости ξ _i нелинейные функции в (6.41) можно разложить в ряд около состояния равновесия;

.

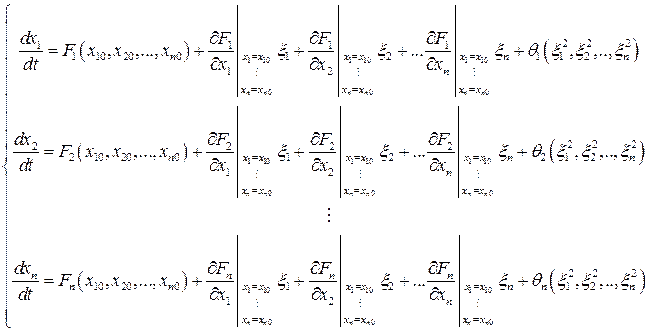(6.46)

где - нелинейные члены, порядок малости которых не меньше . Постоянные составляющие равны нулю в состоянии равновесия (6.23).

Отбрасывая нелинейные члены , , 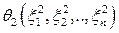…, , получим систему первого приближения;

. (6.47)

Легко увидеть, что система первого приближения (6.47) ничем не отличается от линейной системы (6.23), устойчивость которой исследована выше.

Ляпунову принадлежат три фундаментальных теоремы об устойчивости равновесия нелинейной системы. Сформулируем их без доказательств.

1. Теорема об устойчивости по первому приближению

Если все корни характеристического уравнения системы первого приближения (6.47) имеют отрицательные вещественные части, то соответствующее состояние равновесия нелинейной системы (6.41) асимптотически устойчиво.

Другими словами, из асимптотической системы первого приближения следует асимптотическая устойчивость исходной системы.

2. Теорема о неустойчивости по первому приближению

Если среди корней характеристического уравнения системы первого приближения (6.47) встречается хотя бы один корень с положительной вещественной частью, то состояние равновесия нелинейной системы неустойчиво.

3. Теорема об особенных случаях

Если среди корней характеристического уравнения системы первого приближения (6.47) встречается хотя бы один корень с нулевой вещественной частью, то невозможно сделать заключение об устойчивости или неустойчивости равновесия нелинейной системы.

Чтобы решить вопрос об устойчивости в особенных случаях, необходимо учитывать, по крайней мере, второе приближение в уравнениях (6.46). Однако уравнения возмущенной системы становятся нелинейными и трудности анализа резко возрастают.

Значение теорем Ляпунова для практики огромно. Еще до проведения эксперимента можно найти и проанализировать устойчивые стационарные состояния нелинейной системы, которые будут осуществляться в действительности.

Проиллюстрируем второй метод Ляпунова на примере исследования устойчивости маятника с затуханием. Динамическое уравнение системы при любых углах отклонения имеет вид:

, (6.48)

где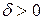

Приведем уравнение (6.48) к стандартной форме. Пусть

. (6.49)

Тогда

. (6.50)

Уравнение (6.48) преобразуется к виду

. (6.51)

Из (6.51) найдем состояние равновесия

. (6.52)

Отсюда 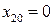, а из получим, что , где n = 0, ±1, ±2, …. Физический смысл имеют два положения равновесия:

1. , - маятник в нижнем положении,

2. - маятник в верхнем положении.

1. Исследуем нижнее состояние равновесия: .

Тогда из (6.45) получим:

. (6.53)

Подставляем в (6.51) и раскладываем в ряд (см.(6.46));

. (6.54)

Отбросим нелинейные члены и получим систему первого приближения;

. (6.55)

Матрица коэффициентов уравнения первого приближения:

. (6.56)

Характеристическое уравнение получим, раскрыв детерминант (6.30):

. (6.57)

Применим критерий Рауса-Гурвица. Матрица Гурвица:

. (6.58)

Определители Гурвица:

. (6.59)

Поскольку 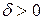и необходимое и достаточное условие выполняются. Следовательно, для любого корня. На основании первой теоремы Ляпунова делаем вывод об асимптотической устойчивости нижнего положения равновесия маятника.

II. Исследуем устойчивость верхнего состояния равновесия:

. (6.60)

Дадим возмущение

. (6.61)

Разложим правые части уравнений (6.51) в ряд:

, (6.62)

и найдем систему первого приближения:

. (6.63)

Характеристическое уравнение будет иметь вид:

. (6.64)

Необходимое условие критерия Рауса-Гурвица нарушено, так как последний коэффициент характеристического уравнения отрицательный, следовательно, , хотя бы для одного корня. На основании второй теоремы Ляпунова об устойчивости делаем вывод, что верхнее положение равновесия маятника неустойчиво.

В качестве второго примера использования методологии Ляпунова рассмотрим вопрос о своеобразной неустойчивости равновесия в области застоя для системы с кулоновским трением (Рис.44).

Исследование проведем на фазовой плоскости. Если отклонение , то движение отсутствует, система находится в состоянии равновесия. Следует идее Ляпунова, дадим возмущение. Для простоты и наглядности рассуждений будет считать, что возмущению подвергается лишь скорость, причем величина возмущения будет одинакова во всех случаях, а знак скорости меняется от опыта к опыту.

Рассмотрим движение изображающей точки, если есть одно положительное и одно отрицательное возмущение скорости. Пусть из состояния равновесия система переводится в состояние ), откуда со временем переходит в новое состояние равновесия .

Состояние равновесия обладает своеобразной «неустойчивостью» - система, выведенная из него, обратно в него же не возвращается.

То же самое можно сказать и о состоянии . Если система получит возмущение по скорости (в этом опыте отрицательное), то она переходит в новое состояние равновесия . Интересно отметить следующее; после двух разных по знаку возмущений по скорости изображающая точка приблизилась к середине области застоя – началу координат. Приближение к началу координат можно исследовать аналитически, доказав неравенство

. (6.65)

В верхней полуплоскости изображающая точка движется по эллипсу (5.40)

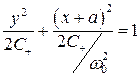, (6.66)

где С ₊ определяется из условия: при и

. (6.67)

При , и из (5.40)

. (6.68)

Взяв разность (6.67) и (6.68), преобразуя, получим

. (6.69)

В нижней полуплоскости изображающая точка движется по эллипсу (5.40)

. (6.70)

При , , тогда

. (6.71)

При , , тогда

. (6.72)

Взяв разность (6.71) и (6.72), получим

. (6.73)

Сравнивая (6.67) и (6.71) и учитывая, что , получаем . Отсюда знаменатель (6.69) больше знаменателя (6.68) и, как следствие, справедливость (6.65).

Придавая возмущение по скорости многократно, при условии равновероятности отклонения, можно приблизиться к положению равновесия (0,0) как угодно близко. Середина области застоя соответствует асимптотически устойчивому состоянию равновесия.

Этот факт используется на практике. Известно, что стрелочные электроизмерительные приборы не выставляются на точный нуль после измерения, что обусловлено кулоновскими трениями в подшипниках. Слегка постукивая по прибору, т.е. давая возмущение по скорости, удается перевести стрелку в абсолютное состояние равновесия и этим повысить точность отсчета.

Поиск по сайту: