Применение графов для описания систем

Сферой приложения топологических методов и теории графов являются системы, состоящие из объектов разнообразной природы. При описании таких систем можно выделить два непересекающихся множества, так что элементы одного из них по определенному закону связаны между собой элементами другого. Речь может идти о множестве переменных и множестве функционалов, устанавливающих связь между переменными математической модели исследуемой системы. Чтобы определить граф, следует задать множества вершин и ребер, а также закон (предикат), устанавливающий взаимную принадлежность (инциденцию) элементов этих множеств. Считают, что граф

(П.1)

задан, если даны непустое множество вершин , не пересекающееся с ним множество ребер и предикат (инцидентор) 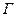. Обычно 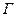является трехместным предикатом, т. е. определенным на всех упорядоченных тройках - и , для которых и 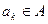. Аналитически предикат описывается логическим высказыванием следующего вида:

, (П.2)

которое означает, что ребро соединяет вершины и . Вершины и называются смежными, а ребро - инцидентным этим вершинам в графе.

Графически граф принято изображать совокупностью точек, взаимно однозначно соответствующих элементам множества вер­шин , и связывающих их линий, взаимно однозначно соответствующих элементам множества ребер . В начертании графа существует определенная свобода (на чертеже ребра графа соединяющие две вершины могут изображаться прямыми или кривыми, короткими или длинными непрерывными линиями), а также - в выборе места положения на чертеже вершин графа.

Согласно определению графа (П.1), для всякого элемента 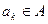справедливо одно и только одно из следующих высказыва­ний:

& & ; (П.3)

(П.4)

& & . (П.5)

Логические высказывания (П.3) - (П.5) позволяют классифицировать ребра на ориентированные (направленные) ребра - дуги (П.3), петли - (П.4) и неориентированные (ненаправленные) ребра - звенья (П.5). В ряде практических случаев звенья в соответствии с высказыванием (П.5) изображаются совокупностью двух (слитых в одну) двунаправленных дуг,

,

что бывает удобно для описания макромоделей систем.

При описании физических систем и процессов, каждому ребру ставится в соответствие вес , именуемый весом ребра и равный конкретной физической величине. Что касается вершин графа, они отождествляются с переменными, описывающими модель системы.

Элементами графа могут быть цепи и циклы. Цепью называется последовательность

элементов графа, для которой справедливо высказывание

.

Циклом графа называется замкнутая цепь . Особое значение при описании систем с помощью графов играют такие их элементы, как путь и контур. Путем из вершины в вершину называется конечная цепь

(П.6)

для которой истинно высказывание

.

В качестве количественных характеристик пути для описания систем уместно использовать такие понятия, как длина пути и вес пути . Число ребер, образующих путь, называется длиной пути. Для пути (2.6) длина 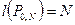. Вес пути - произведение весов образующих его ре­бер, для пути (2.6) вес

.

Путь может быть конечным и бесконечным; он называется про­стым, если в нем ни одно ребро не встречается дважды. Путь , в котором ни одна из вершин не встречается дважды, называется элементарным. При описании систем обычно используют простые элементарные пути.

Замкнутый путь называется контуром . Согласно выражению (П.6) для контура . Определения длины и веса 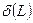контура аналогич­ны соответствующим определениям, сделанным выше для пути. Контур называется простым, если все его рёбра различны, или составным (сложным) - в противном случае. Контур называет­ся элементарным, если все его вершины различны.

Для описания свойств систем следует применять элементарные кон­туры, которые в дальнейшем будем называть просто контурами. Для таких контуров, как и для путей (исключая начальную и ко­нечную вершину), истинно высказывание, утверждающее, что каждая вершина инцидентна двум дугам, причем для одного из них она является конечной, а для другого начальной, т. е.

,

,

где - число дуг, исходящих из вершины ; - число дуг, входящих в вершину .

Элементами графов являются деревья и прадеревья. Деревом называется граф, не содержащий циклов. Ребра, дополняющие дерево, называются хордами. Прадеревом называется дерево, в котором каждая вершина (за исключением одной , именуемой корнем прадерева) является конечной только для одной дуги, т. е.

.

Весом прадерева называется произведение весов всех входящих в него дуг.

Частным случаем прадерева является звезда - совокупность простых путей с общей конечной или на­чальной вершиной; эту вершину назовем центром звезды. Если центром звезды является начальная вершина путей , т.е.

,

где - число путей, образующих звезду , то такую звезду на­зовем расходящейся. В противном случае, если центр звезды является конечной вершиной образующих путей , т.е.

,

то звезду назовем сходящейся. Кроме того, назовем простой звезду, каждый путь которой имеет длину, равную единице.

Любой вершине, не являющейся центром звезды, инцидентны только одна исходящая и одна входящая дуги. Именно такие звезды и прадеревья будут использованы далее для структурной оценки систем.

Далее рассмотрим части графов. Пусть имеем два графа

и ,

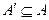где и ; - предикат, индуцированный инцидентором 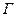на множествах и . Если

,

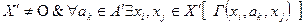то является частью . К числу частей относится и сам граф ; прочие его части обычно называют собственными. Для практики наибольшее значение имеют следующие два типа частей графа. Подграфом графа называется часть графа , порожденная подмножеством вершин , если подмножество ребер 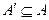удовлетворяет следующему условию:

.

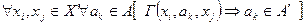То есть при образовании подграфа сохранены все реб­ра исходного графа, которые соединяют между собой подмноже­ство вершин . Суграфом называется часть графа, порожденная подмножеством ребер 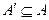при , т.е. при образовании суграфа сохранено множество вершин исходного графа и исключе­ны некоторые ребра. Разновидностью суграфа можно считать прадеревья и элементарные графы, веса которых определяют слагаемые симметричных и несимметричных алгебраических до­полнений определителей линейной системы.

Если является суграфом графа , то сам граф называется сверхграфом; если - подграф, то - надграф, и если - часть графа, то - объемлющий граф.

Существуют конечные и бесконечные графы. По, виду ребер различают неориентированные и ориентированные графы, которые соответственно состоят только из неориентированных и ориентированных ребер. Смешанным графом называется граф, имеющий как ориентированные, так и неориентированные ребра. Ориентированный граф , не содержащий петель, удовлетворяет соотношению

,

где 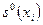- число петель, инцидентных вершине .

Униграфом называется граф , не содержащий кратных ре­бер, т. е. такой, что каждая пара его вершин соединена не более чем одним ребром:

,

где 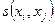- число ребер, соединяющих вершины и .

Граф, не являющийся униграфом, называется мультиграфом.

Когда никакая пара вершин не соединена более чем ребрами , т.е.

,

граф называется - графом. Отсюда следует, что - граф – это пустой граф, а - граф – это униграф.

Объединением графов называется граф , для которого

и предикат 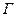индуцирован предикатами .

Пересечением графов следует считать граф , в котором

и предикат 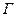индуцирован предикатами .

Известны также и другие операции над графами, которые под­робно изложены в.

Для ориентированного графа существует понятие сильной связности вершин и . Эти вершины являются сильно связанными, если имеется хотя бы один путь из вершины в вершину или наоборот. Соответственно сильно связанным орграфом на­зывается граф, в котором любые две вершины сильно связаны.

Для графов мож­но поставить задачу выяснения тождественности (задачу идентификации) друг друга двух и более графов. В этой связи приме­няется понятие изоморфизма, учитывающее, что в ряде случаев графы могут различаться лишь способом упорядочения ребер-(дуг). Иными словами, условием изоморфизма двух графов, 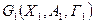и , является наличие взаимно одно­значных соответствий 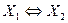; таких, что вершины соединены ребрами в одном из графов в том и только в том случае, когда соответствующие им вершины соединены в другом графе.

Планарным называется граф, если он может быть графически изображен на плоскости так, что все пересечения его ребер являются лишь вершинами графа. В противном случае граф называется непланарным.

Граф считается заданным, если определена пара множеств, и , и трехместный индентор 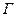. Следовательно, задание графа требует трехмерной таблицы истинности. Описывая 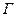посредством трех двухместных предикатов, можно обойтись тремя двумерными таблицами. Использование пятизначной логики позволяет ограничиться только одной двумерной таблицей, например матрицей инциденций с помощью которой однозначно может быть определена топология всякого графа с пронумерованными вершинами и ребрами.

Используются также матрицы соседства, сечений и контуров. Однако недостаток вышеописанных матриц заключается в том, что они отражают только наличие или отсутствие инциденции между вершинами и ребрами и не учи­тывают веса ребер, которые зачастую присваиваются каждому из этих элементов при описании реальных объектов (в частности, ИО). В этом отношении более удобной следует считать мат­рицу , элементы которой определяются следующими соотноше­ниями:

;

,

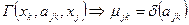где - униграф, описываемый матрицей ; 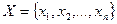. Назовем звездной матрицей графа. Нетрудно заметить, что есть квадратная матрица размерности . При этом диагональные элементы звездной матрицы соот­ветствуют весам петель 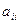в узлах , а недиагональные элемен­ты, расположенные на пересечении - ой строки и -го столбца, со­ответствуют весам дуг , связывающих вершину с вершиной . В общем случае строка матрицы содержит веса петли и входящих в вершину дуг:

. . .

. . .

. . .

…

…

…

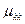
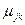
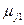
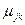
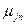
Данной строке соответствует сходящаяся простая звезда с петлей в ее центре . Поэтому методика построения графа может быть сведена к последовательности построения сходящих­ся простых звезд и петель в каждом узле с последующим их объ­единением. Аналогично в общем случае столбцу матрицы соответствует расходящаяся простая звезда с петлей в ее центре . Отсюда всякий орграф может быть построен путем объединения расходящихся простых звезд и петель, сформированных для каждой его верши­ны отдельно.

Достоинством матрицы следует также считать ее соответствие системе однородных уравнений, широко применяемой для описания систем,

(П.7)

или в матричной форме

,

где - вектор переменных, соответствующих вершинам.

Система уравнений (П.7) широко используется при описании линейных систем При этом возможно отождествление уравнений (П.7), звездной матрицы и соответствующего ей графа, которые используются в качестве моделей исследуемых объектов.

К достоинствам матрицы следует отнести также ее удоб­ство для формирования контурных и древесных суграфов, необ­ходимых при вычислении симметричных и несимметричных алгеб­раических дополнений определителей описываемой линейной си­стемы. С использованием метода обобщенных чисел процедура формирования таких суграфов может быть автоматизирована.

Методология построения графов по уравнениям включает в себя два этапа. Первый этап предусматривает преобразование уравнения к виду, который определяет в дальнейшем тип используемого графа. На втором этапе устанавливается взаимно однозначное соответствие между переменными и вершинами подграфа, а также между коэффициентами и весами ребер подграфа. Вышеописанная процедура повторяется столько раз, сколь­ко имеется уравнений, или, иными словами, на сколько компонентов звездного или контурного вида разделен анализируемый объект. Объединение полученных подграфов позволяет получить граф как модель всего объекта.

В этом случае системы уравнений могут быть записаны в виде сле­дующего матричного соотношения:

,

где , - квадратная матрица коэффициентов; , 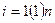и , 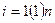- -мерные векторы-столбцы независимых переменных и .

Коэффициенты (параметры информационных потоков) могут зависеть от и .

Часто встречается на практике при линейном моделировании, в т.ч. ИО, уравнение типа

, (П.8)

где - входная переменная; - выходная переменная.

Для аналоговых интегрирующих и дифференцирующих операций также справедливо (2.8) при и соответственно, где - оператор Лапласа; - постоянная времени звеньев.

Примером также может служить сумматор, описываемый уравнением

(П.9)

где - входные, а - выходные напряжения сигнала; - коэффициенты суммирования.

Вышеуказанные уравнения предназначены для описания аналоговых систем и процессов. Вместе с тем представляет интерес рассмотрение дискретных моделей систем. Фундаментальной основой для их описания являются разностные уравнения, которые в общем виде могут быть записаны следующим образом:

(П.10)

где - значение входного сигнала в момент времени ; - значение выходного сигнала в момент времени ; 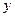- выходной сигнал в момент 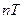времени ; - период квантования сигнала по времени.

Выражение (П.10) называется рекурсивным. Нерекурсивным (П.10) станет, если принять при .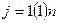

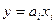Уравнение (П.10) аналогично по форме записи выражениям (П.8) и (П.9). Поэтому дискретные модели обычно рассматривают как системы, состоящие из унифицированных звеньев задержки, описы­ваемых уравнением , а также умножителей или 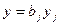и сумматоров (П.10), которые при анализе отображаются простейшими дугами с весами ребер 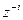, и .

Наиболее распространенной моделью, нашедшей свое при­менение при анализе технических систем, следует считать граф Мэзона, именуемый также сигнальным. Он соответствует системе описыва­ющих цепь линейных уравнений и включает в себя совокупность вершин, отображающих искомые и задающие переменные, и сово­купность дуг, отображающих коэффициенты уравнений.

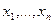Пусть система состоит из уравнений с искомыми переменными и задающими переменными , т.е.

Граф Мэзона строится на основании причинно-следственной формы исходных уравнений:

(П.11)

Вершины графа, соответствующие переменным , называют истоками. Каждая дуга графа имеет норми­рованный вес 1 или , поэтому такая форма представле­ния сигнального графа получила название нормализованной. Су­ществует еще одна форма представления графа Мэзона, которой соответствуют следующие уравнения:

(П.12)

При переходе от выражения (П.12) к графу в вершинах по­являются петли с весами , а веса дуг не нормируются по отношению к весу вершины 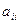. В ряде случаев это бывает более удобно, например, при расчете функций чувствительности

Процедура поиска взаимосвязи между некоторыми вершинами графа, отображающими соответствующие переменные исследуемых систем. Эта процедура позволяет привести исходный граф к эквивалентному графу, содержащему только вершины за­дающих и искомых переменных, связанных минимальным коли­чеством дуг. В результате находится аналитическая зависимость между задающими и искомыми переменными, функционально об­условленная инциденцией и весами дуг графа. Различают три спо­соба поиска взаимосвязи переменных в графах.

Прямой способ основан на свойствах графов и заключается в том, что исходный граф путем последовательных упрощений сводится к графу с желаемым набором вер­шин и дуг. Процедура последовательных упрощений реализуется по специальным правилам преобразования графов. Впервые правила преобразования были разработаны для сиг­нальных нормализованных графов и отражали эквивалентные операции над линейными уравнениями. Основные правила преоб­разований сигнальных графов описаны в работа.

Косвенный способ позволяет получить решение непосредственно из графа без эквивалентных его упрощений. Данный способ, по сравнению с прямым способом, в подавляющем большинстве случаев явля­ется более экономичным, так как позволяет, минуя трудоемкие операции преобразования графов, получить передаточную функ­цию (коэффициент передачи).

Комбинированный способ по­иска взаимосвязи переменных в графах заключается в последовательном частичном применении прямого и косвенного способов. Обычно на первом этапе граф с помощью соответствующих преобразований приводится к виду, удобному для реализации второго этапа, на котором рассчитыва­ют передаточную функцию.

То­пологическая формула передачи может быть записана в следу­ющем обобщенном виде:

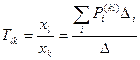, (П.13)

где - номер вершины-истока, соответствующей переменной ; - номер вершины-стока, соответствующей переменной ; 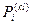- вес некоторого -го пути из вершины в вершину ; - определитель дополняющего путь подграфа, образованного из исходного путем удаления вершин и дуг, принадлежащих - му пути; - определитель исходного графа.

Для различных типов графов все пути 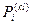равен

,

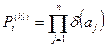где - вес -й дуги графа, образующей -й путь из вершины в вершину ; - число дуг, входящих в состав -го пути из вершины в вершину .

При вычислении определителей может быть использована сле­дующая обобщенная формула:

, (П.14)

где 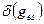- вес -го элементарного графа, образованного из исходного графа по специальным правилам, обусловленным типом графа; - число всевозможных элементарных графов, образован­ных на исходном графе. При этом вес элементарного графа из вы­ражения (П.14) равен

, (П.15)

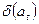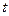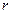где - вес -й дуги графа, образующей -й элементарный граф ; - число дуг, входящих в состав -го элементарного графа; 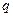- натуральное число, обусловленное типом графа и некоторыми количественными показателями -го элементарного графа.

Выражения (П.14) и (П.15) справедливы также и для опреде­лителя дополняющего подграфа . Как видно из формул (П.13) - (П.15), специфика используемого для расчета графа играет роль лишь при формировании (П.14) и расчете весов (П.15) элементар­ных графов. Рассмотрим эту процедуру для различных типов гра­фов.

Для графа Мэзона элементарный граф состоит из множества некасающихся контуров; фактор 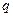равен количеству некасающихся контуров, входящих в состав данного элементарно­го графа. Вес элементарного графа в этом случае

, (П.16)

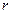где - вес -го контура, входящего в состав данного элементарного графа.

Из (П.15) следует

, (П.17)

где - вес -й дуги, входящей в состав 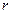-го контура; - длина 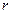-го контура. Следует заметить, что исходный граф может содержать несколько элементарных графов с одним и тем же фактором. Исключение составляет единственный элементарный граф с фактором , который следует считать множеством контуров, вырожденных в вершину, имеющую вес, равный 1. Поэтому с учетом (П.16), (П.17) формула для расчета определителя сигнального графа (Мэзона) часто записывается в следующем виде:

, (П.18)

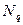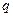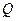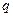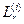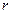где - число элементарных графов с фактором ; - максимальное значение фактора , при котором элементарный граф не является пустым множеством контуров; вес -го контура, принадлежащего -му элементарному графу с фактором .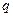

Поиск по сайту: