 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Общее понятие предела переменной величины
Рассмотрим некоторую последовательность, зависящую от натурального аргумента xn=f(n) (n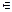 
N), например: хn=2+(-1)n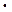 
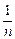, т.е.{1; 2,50; 1,67; 2,25; 1,80,...}:
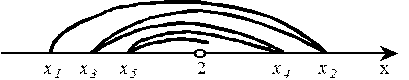
Легко заметить, что при возрастании n члены последовательности все ближе подходят к значению А=2. Если вокруг этого значения выделить какую-то область радиусом e (e-окрестность), то при некотором n xn войдет в эту окрестность и уже не выйдет из нее, какой бы малой она ни была. Это и означает, что А - предел, к которому стремится последовательность хn.
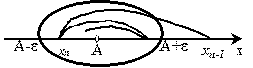
Так что, если в некотором процессе изменение xn таково, что в какой-то момент он попадает в e-окрестность числа А и не выходит из нее, то А - предел величины xn:
.
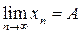Рассмотрим последовательность xn = n, n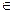 
N, т. е. {1; 2; 3;... }.
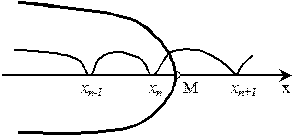
Здесь другой случай: если задаться любым числом М, то всегданайдется такое число n, что xn+1 будет больше М. Эта последовательность не имеет предела. Условно записывают:
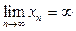
и называют xn бесконечно большой
Для последовательности хn= 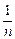, n Î N, т.е. {1; 
; 
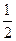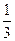;...} при возрастании номера n пределом является А=0, т.е. 
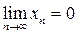. Если предел равен 0, то величина называется бесконечно малой.
Последнее, что отметим: переменная, зависящая от натурального аргумента, может иметь только один предел.
Предел функции
Пусть теперь для некоторой функции у=f(х) процесс таков, что х стремится к числу а. Выясним, к чему стремится функция у. Если двигаться от 0 к точке х=а, то в некоторый момент войдем в d-окрестность числа а. При этом функция (при движении по графику) будет ограничена по оси оY e-окрестностью, увязанной с d -окрестностью по оси оХ, и неизбежно приходит в точку х=а, принимая значение А.
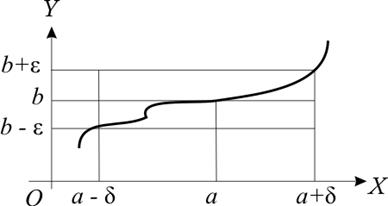
Таким образом, изменение функции у=f(х), в конечном итоге, приводит к тому, что ее значения не выйдут за пределы e-d окрестности точки, которая и является ее пределом:
.
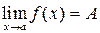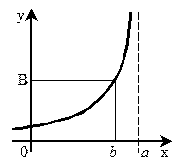
Функция может и не иметь предела. Тогда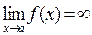 
. Но где-нибудь рядом предел может быть: 
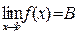. Если 
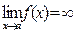, то функция называется бесконечно большой в точке х=а (вариант 
). Если 
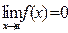, то функция называется бесконечно малой в точке х=а (вариант 
).
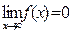Бесконечно малые (б.м.) и бесконечно большие (б.б.) величины
Так как б.м. и б.б. часто встречаются в анализе, то сформулируем их свойства. Для удобства положим a(х) - б.м., b(х) - б.б. величины при х 
а (или х 
).
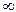1. Если функция у=f(х) может быть представлена суммой постоянного числа А и б.м. величины a(х), т.е. у= А +a, то lim y = A и обратно, если lim y = A, то у =А+a.
2. Сумма нескольких б.м. величин тоже является б.м. величиной.
3. Произведение б.м. величины на ограниченную функцию (или число) также является б.м. величиной.
4. Частное от деления б.м. величины на ненулевую ограниченную функцию (или число) является б.м. величиной.
5. Произведение б.б. величины на ограниченную функцию (или число) также является б.б. величиной.
6. Сумма б.б. величины и ограниченной функции (или числа) является б.б. величиной.
7. Частное от деления б.б. величины на ненулевую ограниченную функцию (или число) является б.б. величиной
8. Величина, обратная б.м. величине, является б.б. величиной: b(х)=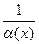 
; Величина, обратная б.б. величине, является б.м. величиной: a(х)= 
.
Поиск по сайту: