Квантовая механика

В квантовой механике также возможно формулирование закона сохранения энергии для изолированной системы. Так, в шредингеровском представлении при отсутствии внешних переменных полей гамильтониан системы не зависит от времени и можно показать^[13], что волновая функция, отвечающая решению уравнения Шредингера, может быть представлена в виде:

Здесь — волновая функция системы, 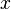— совокупность переменных, от которых зависит состояние системы в данном представлении, — собственные функции и собственные значения оператора Гамильтона, — постоянная Планка, — некоторые постоянные комплексные коэффициенты, характеризующие состояние системы. По определению средней энергией квантовой системы, описываемой волновой функцией, называется интеграл

где — гамильтониан системы. Несложно видеть, что этот интеграл не зависит от времени:

где также использовано свойство ортонормированности собственных функций гамильтониана^[14]. Таким образом, энергия замкнутой системы сохраняется.

Следует, однако, отметить, что по сравнению с классической механикой у квантового закона сохранения энергии имеется одно существенное отличие. Дело в том, что для экспериментальной проверки выполнения закона необходимо провести измерение, представляющее собой взаимодействие исследуемой системы с неким прибором. В процессе измерения система, вообще говоря, более не является изолированной и её энергия может не сохраняться (происходит обмен энергией с прибором). В рамках классической физики, однако, это влияние прибора всегда может быть сделано сколь угодно малым, в то время как в квантовой механике имеются фундаментальные ограничения на то, насколько малым может быть возмущение системы в процессе измерения. Это приводит к так называемому принципу неопределённости Гейзенберга, который в математической формулировке может быть выражен в следующем виде:

,

где имеет смысл среднеквадратичного отклонения измеренного значения энергии от среднего значения при проведении серии измерений, — продолжительность взаимодействия системы с прибором в каждом из измерений.

В связи с наличием этого фундаментального ограничения на точность измерений в квантовой механике часто говорят о законе сохранения средней энергии (в смысле среднего значения энергии, полученного в результате серии измерений).

Поиск по сайту: