Структура оптимизационных задач

Несмотря на то, что прикладные задачи, рассмотренные в предыдущем разделе, относятся к совершенно разным областям инженерной практики и представляют различные системы, они имеют общую форму. Все эти задачи можно классифицировать как задачи минимизации вещественнозначной функции f (х) N-мерного векторного аргумента , компоненты которого удовлетворяют системе уравнений , набору неравенств , а также ограничены сверху и снизу, т. е. 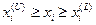. В последующем изложении функцию f(х) будем называть целевой функцией, уравнения — ограничениями в виде равенств, а неравенства — ограничениями в виде неравенств. При этом предполагается, что все фигурирующие в задаче функции являются веще-ственнозначными, а число ограничений конечно.

Задача общего вида:

минимизировать f(х), при ограничениях

называется задачей оптимизации с ограничениями или задачей условной оптимизации. В частности, в примерах1.1, 1.2 и 1.3 рассмотрены задачи условной оптимизации. Задача, в которой нет ограничений, т. е.

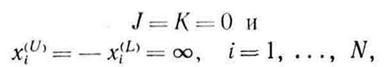
называется оптимизационной задачей без ограничений или задачей безусловной оптимизации. В примере 1.4 представлена задача без ограничений.

Задачи оптимизации можно классифицировать в соответствии с видом функций 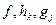f, h.h, g/ и размерностью вектора х. Задачи без ограничений, в которых х представляет собой одномерный вектор, называются задачами с одной переменной и составляют простейший, но вместе с тем весьма важный подкласс оптимизационных задач. Задачи условной оптимизации, в которых функции являются линейными, носят название задач с линейными ограничениями. В таких задачах целевые функции могут быть либо линейными, либо нелинейными. Задачи, которые содержат только линейные функции вектора непрерывных переменных x, называются задачами линейного программирования; в задачах целочисленного программирования компоненты вектора х должны принимать только целые значения. Одна из задач линейного программирования рассмотрена в примере 1.3 (разд. 1.2).

Задачи с нелинейной целевой функцией и линейными ограничениями иногда называют задачами нелинейного программирования с линейными ограничениями. Оптимизационные задачи такого рода можно классифицировать на основе структурных особенностей нелинейных целевых функций. Если f(x) — квадратичная функция, то мы имеем дело с задачей квадратичного программирования; если f(x) есть отношение линейных функций, то соответствующая задача носит название задачи дробно-линейного программирования, и т. д. Деление оптимизационных задач на эти классы представляет значительный интерес, поскольку специфические особенности тех или иныx задач играют важную роль при разработке методов их решения.

Литература к главе 2

1. Zeieny M., Multiple Criteria Decision Making, McGraw-HiU, N.Y., 1982.

2. Vincent Т. L., Grantham W.J., Optimality in Parametric Systems, Wiley, N.Y., 1981.

3. Belt K.E., Rowlinson J.S., Saville G., Thermodynamics for Chemical Engineers, MIT Press, Cambridge, Massachusetts, 1975.

4. Jen F. C., Pegels C. C., Dupuis T. M., Optimal Capacities of Production Facili­ties, Management Sci., 14B. 570—580 (1968).

5. Shigley J. E., Mechanical Engineering Design, McGraw-Hill, N. Y., 1973, p. 271.

6. Timoshenko S., Gere J., Theory of Elastic Stability, McGraw-Hill, N.Y., 1961» p. 257.

7. Ragsdell К. M., Phillips D. Т., Optimal Design of a Class of Welded Structures using Geometric Programming, ASME J. Eng. Ind. Ser. В., 98, (3). 1021—1025 (1975).

8. White W. В., Johnson S. M., Dantzig G. В., Chemical Equilibrium in Complex Mixtures, J..Chem. Phys., 28, 251—255 (1959).

9. Hayt W. H., Kemmerly J. E., Engineering Circuit Analysis, McGraw-Hill, N. Y.» 1971, Ch. 2..

Поиск по сайту: