Эйлеровы и гамильтоновы графы

Эйлеровым путём (циклом) графа называется путь (цикл), содержащий все рёбра графа ровно один раз. Граф, обладающий эйлеровым циклом, называется эйлеровым графом.

На рис. 3.9 граф G не является эйлеровым, т.к. вершина Р₃ инцидентна только одному ребру. Если путь приведёт в вершину Р ₃, то не будет ребра, по которому можно было бы выйти из Р _3.

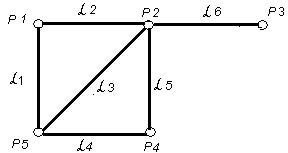
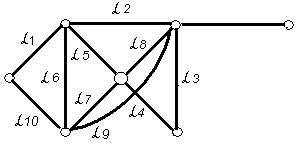
Рис. 3.9 Рис. 3.10

Рис.3.11

Теорема. Граф G является эйлеровым тогда и только тогда, когда G связный и все его вершины имеют чётную степень.

Граф G, изображённый на рис. 3.10, является эйлеровым. Последовательность рёбер ( _{1, 2, 3, 4, 5, 6, 7, 8, 9, 10,}) образуют эйлеровый цикл.

Теорема: Граф G обладает эйлеровым путём с концами Р_1, Р₂ тогда и только тогда, когда G связный и Р_1, Р₂ - единственные его вершины нечётной степени.

На рис. 3.9 изображён граф G, обладающий эйлеровым путём ( _{1, 2, 3, 4, 5, 6}) с концевыми вершинами Р₅ и Р_{3 .}

Гамильтоновым путём (циклом) графа называется путь (цикл), проходящий через каждую вершину графа в точности по одному разу. Граф, обладающий гамильтоновым циклом, называется гамильтоновым графом.

Критерий существования гамильтонова цикла в произвольном графе G ещё не найден. Достаточным условием существования гамильтонова цикла является полнота графа G.

Граф на рис. 3.9. не является гамильтоновым, а граф на рис.3.11 содержит гамильтонов цикл (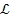 _{1, 2, 4, 5, 6}).

Поиск по сайту: