 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Кручение
|
Читайте также: |
2.4.1. Общие сведения о деформации кручения
Наглядное представление о деформации кручения дает действие двух равных и противоположно направленных крутящих моментов (рис.2.20).


Рис.2.20.Деформация кручения
В результате деформации образующие вала получают вид винтовых линий. Такой вид получают образующие валы и в случае следующего закрепления (рис.2.21).

Рис. 2.21. Деформация вала
При действии крутящего момента М все линии рассматриваемой образующей будут отклоняться от первоначального положения на некоторые углы по окружности. На основе этого можно сделать выводы:
1. При кручении, в каждом сечении вала происходит поворот точек по окружности относительно оси. Следовательно, вал испытывает кручение, если к нему прикладывается пара сил направленных перпендикулярно осям.
 2. Под действием внешних моментов, в поперечном сечении вала, возникает единственная составляющая главного момента, а именно крутящий момент Мк (рис. 2.22).
2. Под действием внешних моментов, в поперечном сечении вала, возникает единственная составляющая главного момента, а именно крутящий момент Мк (рис. 2.22).

Рис.2.22. Главный момент
3. Деформация кручения вала заключается в повороте поперечных сечений относительно друг друга, при этом углы поворота прямопропорциональны растяжению.
4. Угол поворота рассматриваемого сечения равен углу закручивания части вала, которая заключена между данным сечением и заделкой. Угол кольцевого сечения называется углом закручивания вала.
5. В произвольном сечении угол поворота можно оценить относительным углом закручивания:

где  - угол закручивания выделенного элемента;
- угол закручивания выделенного элемента;  - расстояние от рассматриваемого сечения до заделки,
- расстояние от рассматриваемого сечения до заделки,  - относительный угол закручивания.
- относительный угол закручивания.
Если балка длиной l м имеет постоянное поперечное сечение и нагружена внешним моментом на конце вала, то относительный угол закручивания будет:
 = const
= const
6. При кручении вала возникает деформация сдвига между соседними сечениями, следовательно, при кручении поперечных сечений валов, возникают только касательные внутренние силы создающие крутящий момент.
Крутящие моменты в поперечных сечениях вала определяют методом сечений. При использовании уравнений равновесия:
 ;
; 
Крутящий момент в поперечном сечении вала численно равен алгебраической сумме внешних моментов, которые приложены к оставленной для рассмотрения части вала.
 Считаем крутящий момент положительным, если внешний момент по отношению к рассматриваемой части вала направлен по ходу часовой стрелки (рис.23).
Считаем крутящий момент положительным, если внешний момент по отношению к рассматриваемой части вала направлен по ходу часовой стрелки (рис.23).
Рис.2.23. Правило знаков
Эпюра крутящих моментов представляет собой график изменения крутящего момента по длине вала. С помощью эпюры крутящих моментов определяют опасное сечение вала, то есть такое в котором действует наибольший крутящий момент.
2.4.2. Напряжение и деформация при кручении
В поперечных сечениях скрученного вала (рис.2.24) действует, только касательное напряжение 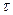 , следовательно, крутящий момент представляет собой результирующий момент внутренних касательных сил, то есть действующий на бесконечно малых площадках поперечного сечения, его можно выразить:
, следовательно, крутящий момент представляет собой результирующий момент внутренних касательных сил, то есть действующий на бесконечно малых площадках поперечного сечения, его можно выразить:
 .
.
где  - расстояние или плечо элементарной силы относительно продольной оси вала;
- расстояние или плечо элементарной силы относительно продольной оси вала;
r –радиус вала.
 Данная зависимость отражает статическую сторону работы сечения, но не позволяет определить значение касательных напряжений по известному крутящему моменту, так как в данном случае не установлен закон распределения касательных напряжений по сечению.
Данная зависимость отражает статическую сторону работы сечения, но не позволяет определить значение касательных напряжений по известному крутящему моменту, так как в данном случае не установлен закон распределения касательных напряжений по сечению.
Рис. 2.24. Схема скрученного вала
Угол сдвига для некоторого поперечного сечения.
 φ0
φ0
где φ0 – угол поворота.
Тогда касательное напряжение прямо пропорционально расстоянию до оси вала.
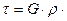 φ0 . (2.21)
φ0 . (2.21)
Эпюра распределения 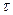 вдоль радиуса сечения вала всегда имеет вид треугольника, если соблюдаются выше перечисленные условия (рис. 2.25). Если вал состоит из одного участка (то есть имеет постоянное сечение и постоянный по длине крутящий момент), то
вдоль радиуса сечения вала всегда имеет вид треугольника, если соблюдаются выше перечисленные условия (рис. 2.25). Если вал состоит из одного участка (то есть имеет постоянное сечение и постоянный по длине крутящий момент), то 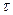 в данном волокне бруса будет постоянным по всей длине участка.
в данном волокне бруса будет постоянным по всей длине участка.

Рис. 2.25. Эпюра касательных напряжений 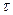
2.4.3. Расчет на жесткость и прочность при кручении
1. Прочность 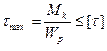 , (2.22)
, (2.22)
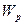 - полярный момент сопротивления [
- полярный момент сопротивления [ 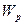 ] = [м3]
] = [м3]
 - допускаемое касательное напряжение, устанавливается в зависимости от допускаемого напряжения при растяжении.
- допускаемое касательное напряжение, устанавливается в зависимости от допускаемого напряжения при растяжении.
2. Условие жесткости бруса при кручении состоит в том, чтобы относительный угол закручивания φ0 не превосходил некоторого заданного допускаемого значения [φ0]
φ0 ≤ [φ] – условие жесткости; (2.23)
где φ0 – относительный угол закручивания;
[φ] – допускаемый относительный угол закручивания.
φ0 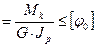 ; [φ0] = 0,2…1; [
; [φ0] = 0,2…1; [ 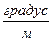 ] (2.24)
] (2.24)
2.4.4. Пример расчета вала при кручении
Для стального трансмиссионного вала (рис. 2.26) G = 8·1010 МПа:
1. Определите значение скручивающих моментов (подводимого к шкиву 0 и снимаемых со шкивов 1, 2, 3).
2. Постройте эпюры крутящих моментов.
3. Определите диаметры каждого участка ступенчатого вала из условия прочности. Окончательно принимаемые значения должны быть округлены до ближайших стандартных по ГОСТ 6636-69. Диаметр вала (мм): 30, 35, 40, 45, 50, 60, 70, 80, 90, 100, 110, 125, 140, 160, 180, 200.
4. Вычертите в масштабе эскиз ступенчатого вала.
5. Постройте эпюру углов закручивания относительно левого шкива на валу.
6. Проверьте жесткость вала при кручении и при недостаточной жесткости участков вала, определите их диаметры из условий жесткости.
Числовые данные варианта взять из приложения 11, схему варианта из приложения 12.
Схема нагружения и исходные данные.

Рис. 2.26. Схема нагружения
ИСХОДНЫЕ ДАННЫЕ
| а | Р0 | Р1 | Р2 | Р3 | ω | [τ] | [φ] |
| м | кВт | рад/с | мПа | рад/м | |||
| 0,1 | 0,02 |
 |
Рис. 2.27. Расчетная схема и результаты расчетов
Поиск по сайту: