Транспортная задача

Транспортная задача - это задача о выборе плана пе­ревозок однородного продукта из пунктов производства в пункты потребления.

Пусть имеется т пунктов отправления и п пунктов назначения. Запасы продукта в пунктах отправления обо­значим через а_ij потребность в продукте в пункте потребле­ния - b_j Расходы на доставку единицы продукта из i -го пункта отправления в j -й пункт назначения равняются С_ij.

Теорема. Для разрешимоститранспортной задачинеобходимо и достаточно, чтобы запасы груза в пунктах отправления были равны потребности в грузе в пунктах назначения, т.е. чтобы выполнялось равенство

(1)

Модель такой транспортной задачи называется закрытой, или замкнутой, или сбалансированной, в противном случае модель называется открытой.

В случае 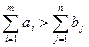вводится фиктивный -й пункт назначения с потребностью и соответствующие тарифы считаются равными нулю: 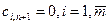; аналогично, при вводится фиктивный -й пункт отправления с запасом груза и соответствующие тарифы считаются равными нулю: . Этим задача сводится к обычной транспортной задаче. В дальнейшем будем рассматривать закрытую модель транспортной задачи.

Требуется определить х_ij - количество продукта, достав­ляемого от i -го пункта отправления к j -му пункту потребле­ния. При этом обязательными условиями являются: необходимость вывоза всего произведенного продукта, необходимость удовлетворения всех потребителей, оптимальный план доставки продукта должен обеспечить минимум общей суммы затрат на доставку. Экономико-математическая модель задачи:

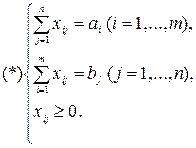
В рассмотренной ЭММ предполагается, что суммарные запасы равны суммарным потребностям.

При решении транспортной задачи выбор критерия оптимальности имеет важное значение. Как известно, оценка экономической эффективности примерного плана может определятся по тому или иному критерию, положенного в основу расчета плана. Этот критерий является экономическим показателем, характеризующим качество плана. До настоящего времени нет общепринятого единого критерия всесторонне учитывающего экономические факторы. При решении транспортной задачи, в качестве критерия оптимальности в различных случаях используют следующие показатели:

1) объем работы транспорта (критерий - расстояние в т/км). Минимум пробега удобен для оценки планов перевозок, поскольку расстояние перевозки определяется легко и точно для любого направления. Поэтому критерию нельзя решать транспортные задачи с участием многих видов транспорта. С успехом применяется при решении транспортных задач для автомобильного транспорта. При разработке оптимальных схем перевозки однородных грузов автомобилями;

2) тарифная плата за перевозку груза (критерий - тарифы провозных плат). Позволяет получить схему перевозок, наилучшую с точки зрения хозрасчетных показателей предприятия. Все надбавки, а также существующие льготные тарифы затрудняют его использование;

3) эксплутационные расходы на транспортировку грузов (критерий - себестоимость эксплутационных расходов). Более верно отражает экономичность перевозок различными видами транспорта. Позволяет делать обоснованные выводы о целесообразности переключения с одного вида транспорта на другой;

4) сроки доставки грузов (критерий - затраты времени)

5) приведенные затраты (с учетом эксплуатационных расходов, зависящих от размеров движения и капиталовложения в подвижной состав);

6) приведенные затраты (с учетом полных эксплуатационных расходов капиталовложений на строительство объектов в подвижной состав);

,

где - эксплутационные издержки; -расчетный коэффициент эффективности капиталовложения; 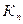- капитальные вложения, приходящие на 1 т груза на протяжении участка; Т - время следования; Ц - цена одной тоны груза.

Транспортная задача может быть решена следующими методами: метод северо-западного угла (диагональный метод), метод наименьшей стоимости (минимального элемента), метод двойного предпочтения и метод аппроксимации Фогеля.

Кратко рассмотрим каждый из них.

1. Метод северо-западного угла. При нахождении опорного плана на каждом шаге рассматривают первый из оставшихся пунктов отправления и первый из оставшихся пунктов назначения. Заполнение клеток таблицы условий начинается с левой верхней клетки для неизвестного («северо-западный угол») и заканчивается клеткой для неизвестного 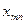, т.е. как бы по диагонали таблицы.

2. Метод наименьшей стоимости. Суть метода заключается в том, что из всей таблицы стоимостей выбирают наименьшую и в клетку , которая ей соответствует, помещают меньшее из чисел и , затем из рассмотрения исключают либо строку, соответствующую поставщику, запасы которого полностью израсходованы, либо столбец, соответствующий потребителю, потребности которого полностью удовлетворены, либо и строку и столбец, если израсходованы запасы поставщика и удовлетворены потребности потребителя. Из оставшейся части таблицы стоимостей снова выбирают наименьшую стоимость, и процесс размещения запасов продолжают, пока все запасы не будут распределены, а потребности удовлетворены.

3. Метод двойного предпочтения. Суть метода заключается в следующем. В каждом столбце отмечают знаком «√» клетку с наименьшей стоимостью. Затем то же проделывают в каждой строке. В результате некоторые клетки имеют отметку «√√». В них находится минимальная стоимость, как по столбцу, так и по строке. В эти клетки помещают максимально возможные объемы перевозок, каждый раз исключая из рассмотрения соответствующие столбцы или строки. Затем распределяют перевозки по клеткам, отмеченным знаком «√». В оставшейся части таблицы перевозки распределяют по наименьшей стоимости.

4. Метод аппроксимации Фогеля. При определении опорного плана данным методом на каждой итерации по всем столбцам и всем строкам находят разность между двумя записанными в них минимальными тарифами. Эти разности заносят в специально отведенных для этого строке и столбце в таблице условий задачи. Среди указанных разностей выбирают максимальную. В строке (или столбце), который данная разность соответствует, определяют минимальный тариф. Клетку, в которой он записан, заполняют на данной итерации.

Перечисленные методы очень громоздки и требуют большого объема вычислительных работ. Поэтому для решения транспортных задач используют более простые методы. Наиболее часто применяются метод потенциалов (модифицированный распредели­тельный метод) и метод дифференциальных рент. Наиболее применяемый из них метод потен­циалов.

Этот первый точный метод решения транспортной задачи был предложен в 1949 г. Кантаровичем А.В. и Гавуриным М.К. и по существу является детализацией метода последовательного улучшения плана применительно к транспортной задаче. Однако в начале он был изложен вне связи с общими методами линейного программирования. Несколько позднее аналогичный алгоритм был разработан Данциом, который исходил из общей идеи линейного программирования. В американской литературе принято называть модифицированным распределительным методом. Метод потенциалов позволяет определить отправляясь от некоторого опорного плана перевозок построить решение транспортной задачи за конечное число шагов (итераций).

Согласно методу потенциалов, каждому i -му пункту от­правления устанавливается потенциал U_i, который можно интерпретировать как цену продукта в пункте отправле­ния, а каждому j -му пункту назначения устанавливается потенциал V_j, который можно условно принять как цену продукта в пункте назначения. В простейшем случае цена продукта в пункте назначения равна его цене в пункте отправления плюс транспортные расходы на его доставку, т.е. .

Алгоритм решения транспортной задачи методом по­тенциалов включает следующие этапы:

1) определение начального плана перевозок с помощью метода северо-западного угла, наименьших стоимостей или аппроксимации Фогеля;

2) построение системы потенциалов на основе равен­ства ;

3) проверка начального плана на оптимальность, и в случае его неоптимальности реализация циклов перерас­пределения плана перевозок.

Третий этап повторяется до тех пор, пока план перево­зок не станет оптимальным.

Пример. Пусть имеется 3 поставщика и 4 потребите­ля. Запасы продукта у поставщиков, спрос потребителей и транспортные расходы на доставку единицы продукта от i -го поставщика к j -му потребителю заданы (табл. 10).

Таблица 10

Требуется составить такой план перевозки, чтобы обес­печить минимум общей суммы транспортных расходов.

Решение. Обозначим x_ij - количество продукта, до­ставляемого от i -го поставщика к j -му потребителю. Тогда модель:

Определим начальный план перевозок с помощью мето­да северо-западного угла, по которому транспортная мат­рица заполняется слева направо и сверху вниз. Потреб­ность первого потребителя удовлетворяется за счет первого поставщика. Если потребности оказались выше возможно­стей первого поставщика, то подключаем второго постав­щика. Если запасы первого поставщика больше потребно­стей первого потребителя, то остаток первого поставщика передаем второму потребителю и т.д. (табл. 11).

Мы должны заполнить т + п - 1 клеток. Если число заполненных клеток меньше т + п - 1 (случай вырожде­ния), то недостающие клетки выбираются произвольно и заполняются нулями. Это так называемые условные по­ставки.

Первоначальный план содержит шесть перевозок: от первого поставщика -. 150 ед. к первому потребителю и 20 ед. ко второму; от второго поставщика - 210 ед. ко второму и 40 ед. к третьему; от третьего поставщика - 120 ед. к третьему потребителю и 60 ед. к четвертому.

Таблица 11

Построим систему потенциалов на основе равенства

Присвоим первому поставщику потенциал U₁ = 0. От первого поставщика продукт направляют первому и второ­му потребителям, следовательно, ; . Зная потенциал второго потребителя, най­дем потенциал второго поставщика . Потенциал третьего потребителя . Потенци­ал третьего поставщика . Потенциал четвер­того потребителя . Вычисленные потенциа­лы помещаем в табл. 12.

Таблица 12

Итерация 1. Целевая функция = 2590

Проверим первоначальный план на оптимальность. План считается оптимальным, если для всех свободных ячеек выполняется условие

Осуществляем проверку:

- не выполняется, т.е. если бы продукт отправлялся от первого поставщика к третьему потребителю, то его цена у первого поставщика была бы ниже, чем в первоначальном плане.

Рассчитанные значения заносятся в свободные ячейки табл. 12.

Для улучшения плана (целевая функция = 2690) необ­ходимо переместить перевозку в ячейку, где условие опти­мальности нарушено больше всего, т.е. разность максимальна (ячейка 1.4).

Перемещение производится так, чтобы по отношению к выбранной ячейке образовать связку. Для этого необходимо провести замкнутую ломаную линию, состоящую из горизон­тальных и вертикальных линий, в которой одной из вершин полученного многоугольника является свободная ячейка, а остальные вершины должны находиться в занятых ячейках.

Далее каждой ячейке в связке поочередно присваива­ются знаки плюс и минус, начиная со свободной. Из ячеек со знаком минус перемещаем перевозки в ячейки со зна­ком плюс. Чтобы не получить отрицательных перевозок, перемещаем наименьшее количество продукта, которое на­ходится в ячейках связки со знаком минус.

Последовательное улучшение плана представлено в таб­л. 12-14.

Таблица 13

Итерация 2. Целевая функция = 2570

Таблица 14

Итерация 3. Целевая функция = 2550

Поиск по сайту: