Графы, сети, деревья

Граф – это графическая структура, которая отображает элементный состав системы и структуру связей в этой системе. Например, словесное описание местности «Район со-стоит из 5 поселков – Дедкино, Бабкино, Кошкино, Мышкино, Репкино. Автомобильные дороги проложены между Дедкино и Бабкино, Дедкино и Кошкино, Бабкино и Мышкино, Бабкино и Кошкино, Кошкино и Репкино» может быть представлено в виде графа, изображенного на рис. 22.2

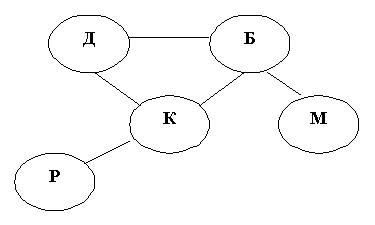
Рисунок 22.2. Неориентированный граф, представляющий структуру описания местности

Составными частями графа являются вершины и ребра. Вершины на рис. 22.2 изображены кружками, изображающими элементы системы, а ребра изображены линиями, показы-вающими связи (отношения) между элементами. Граф, изображенный на рис. 22.2, относится к виду графов, называемому сетью. Для такого вида графов характерна возможность раз-личных путей перемещения по ребрам между некоторыми парами вершин. В сетях возможны так же замкнутые пути, называемые циклами. Граф, изображенный на рис. 22.2, так же является неориентированным графом. В нем каждое ребро обозначает наличие дорожной связи между двумя пунктами. Но дорожная связь действует одинаково в обе стороны: если по дороге можно проехать от Б к М, то по ней же можно проехать от М к Б. Такую связь еще называют симметричной.

Рассмотрим другой пример графа, изображенного на рис. 22.3. На этом рисунке отображено следующее описание предметной области: «У человека существует 4 группы крови. При переливании крови от одного человека к другому не все группы совместимы. Варианты, которые возможны при переливании крови, указаны с помощью графа на рис. 22.3. Группы крови представлены вершинами графа с соответствующими номерами, а стрелки указывают на возможность переливания одной группы крови человеку с другой группой крови». Связи между вершинами данного графа несимметричны и поэтому изображаются направленными линиями со стрелками. Такие линии принято называть дугами (в отличие от ребер неориентированных графов). Граф с такими свойствами называется ориентированным. Ребра, исходящие и входящие в одну и ту же вершину, называются петлями.

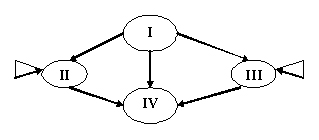
Рисунок 22.3. Ориентированный граф, отображающий описание предметной области «Переливание крови».

При построении информационных моделей многих систем приходится иметь дело с иерархической структурой. В этих структурах установлены отношения подчиненности. На рисунке 22.4 изображен граф, отражающий управления средней школой. Такой ориентированный или неориентированный граф называется деревом. Основными свойствами дерева, отличающими его от других видов графов, является то, что между любыми двумя его вершинами существует единственный путь, и, кроме того, из каждой вершины может выходить несколько ребер, но в каждую вершину входит только одно ребро. Есть вершина, в которую не входит ни одно ребро (корень дерева) и вершины, из которых не выходит ни одного ребра (листья).

Рисунок 22.4. Дерево, изображающее структуру управления средней школой.

Широко известным в информатике примером применения дерева для отображения предметной области является изображение системы хранения файлов и каталогов на магнитных дисках.

Поиск по сайту: