 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Алгоритм решения систем линейных уравнений методом Жордана-Гаусса
1. Из коэффициентов при неизвестных в таблице произвольным образом выбираем разрешающий элемент а ij ¹0. Этот элемент будет определять i -ую разрешающую строку и j -ый разрешающий столбец.
2. Разрешающую строку делим на разрешающий элемент а ij и записываем результат в следующую таблицу.
3. На месте разрешающего элемента а ij в следующей таблице всегда будет находиться единица. Все остальные элементы j -го столбца последующей таблицы будут нулевыми.
4. Все другие элементы последующей таблицы будут рассчитываться с помощью схемы:




 а в 1
а в 1 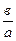


 с d 0 d1
с d 0 d1
Табл.1 Табл. 2
Элемент d1 определяется следующим образом:
 .
.
5. Разрешающий элемент в последующих таблицах определяется так, чтобы разрешающие строка и столбец не повторялись.
6. Переменные, коэффициенты при которых образуют единичную матрицу, будем называть базисным и записывать в соответствующей строке столбца хб.
7. Столбцы хб и вi последней таблицы будут давать решение исходной системы линейных уравнений.
П р и м е р. Решить систему линейных уравнений методом Жордана-Гаусса. 
Решение:
Запишем систему линейных уравнений в виде таблицы:
Таблица 1
| хб | х1 | х2 | х3 | вi |
| -1 | -2 | |||
| -1 | ||||
| -1 |
В качестве разрешающего элемента возьмем коэффициент а11 = 1. Тогда разрешающей будет первая строка и разрешающим будет первый столбец.
Переходим ко второй таблице. Первую строку без изменения (делим на единицу) записываем во вторую таблицу первой строкой. “Разрешающая” единица без изменения перейдет во вторую таблицу. Остальные элементы первого столбца второй таблицы будут нулевыми.
Приведем методику расчета других элементов второй таблицы.
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;

таблица 2
| хб | х1 | х2 | х3 | вi |
| х1 | -1 | -2 | ||

| -4 | |||
| -2 |
Переменная х1 стала базисной, поэтому х1 записывается в столбец хб против соответствующего единичного коэффициента при переменной х1, т.е. в первой строке. В качестве разрешающего выбираем элемент  и переходим к таблице 3.
и переходим к таблице 3.
Таблица 3
| хб | х1 | х2 | х3 | вi |
| х1 | -1 | -1 | ||

| ||||
| х3 | -1 |
После преобразования элементов таблицы 3, получим заключительную таблицу 4.
Таблица 4
| хб | х1 | х2 | х3 | вi |
| х1 | ||||
| х2 | ||||
| х3 | -1 |
Первый и последний столбцы таблицы 4 дают решение системы линейных уравнений.
Ответ: х1 =1; х2 =-1; х3 =2.
Поиск по сайту: