Численные методы решения задачи

(методы одномерного поиска).

Методы одномерного поиска представляют собой вычислительную процедуру, в ходе которой интервал возможных значений изменяется от заданного начального до конечного, не превышающего допустимую погрешность.

При использовании этих методов вычисляется значение целевой функции при 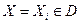, выбирается таким образом, чтобы , где i – номер шага поиска.

Алгоритм поиска должен включать в себя:

- правило перехода от 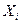к ,

- правило окончания поиска, которое связано с точностью определения , т.е. с величиной заданной допустимой погрешности.

Численные методы решения оптимизационных задач в основном представляют из себя итерационные вычислительные процедуры. Суть итерационных методов расчета заключается в том, что на каждой последующей итерации (этапе) расчета используются результаты, полученные на предыдущей итерации.

В оптимизационных задачах результаты предыдущей итерации используются для того, чтобы уменьшить область (для задач одномерного поиска-интервал), в которой будет искаться максимум на последующей итерации.

К неитерационным методам, где расчеты осуществляются в один этап, относятся методы, позволяющие работать с невыпуклыми функциями, имеющими несколько точек максимума. Одним из таких методов является метод равномерного поиска, рассматриваемый ниже.

Поиск по сайту: