АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Сферична хвиля

Читайте также:
  1. Плоска хвиля

Хвильове рівняння в тримірному просторі припускає інші рішення, які, наприклад, мають сферичну симетрію.

Для цього в хвильовому рівнянні

припустимо, що шукана функція U залежить від двох змінних: віддалі r від точки збудження і часу t:

Для знаходження такого рішення перетворимо таке рівняння до сферичних координат. Враховуючи, що 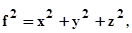знайдемо

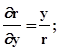
Отже,

Підставляючи в хвильове рівняння,

або

(4.32)

Порівнюючи отримане рівняння з одномірним хвильовим рівнянням (4.25), рішення якого нам відомо, загальне рішення для сферичної хвилі буде таким

(4.33)

Перша складова відповідає розбіжній сферичній хвилі, а друга – збіжній хвилі.



1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 | 51 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)