 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Розділ 14.4. Завдання до заняття 14
 Теоретичні питання до заняття 14
Теоретичні питання до заняття 14
1. За якою формулою обчислюється умовна варіанта?
2. За якою формулою обчислюється середня вибіркова за методом добутків?
3. За якою формулою обчислюється дисперсія за методом добутків?
4. Дати означення статистичної оцінки.
5. Які властивості має статистична оцінка?
6. Яка статистична оцінка називається незміщеною?
7. Яка статистична оцінка називається ефективною?
8. Яка статистична оцінка називається спроможною?
9. За якою формулою обчислюється виправлена дисперсія?
10. Як знайти середню вибіркову при малих обсягах вибірки?
11. Як знайти дисперсію при великих і малих обсягах вибірки?
12. Дати означення довірчої ймовірності.
13. За якою формулою визначається довірчий інтервал для оцінки математичного сподівання генеральної сукупності?
14. За якими формулами визначається довірчий інтервал для оцінки середнього квадратичного відхилення генеральної сукупності?
Розділ 15.1. Статистична гіпотеза (основні поняття)
Існують різні види гіпотез (припущень), але в математичній статистиці виділяють два основних: гіпотези про закон розподілу генеральної сукупності і гіпотези про величину параметра генеральної сукупності.
 Означення: Статистичною називається гіпотеза про вид невідомого розподілу або про параметри невідомого розподілу.
Означення: Статистичною називається гіпотеза про вид невідомого розподілу або про параметри невідомого розподілу.
Поряд з гіпотезою, що висувають, має місце і протилежна до неї гіпотеза, яка вступає з нею в протиріччя. Якщо гіпотезу, що висувається, відкинуто, тоді має місце гіпотеза, що вступає з нею в протиріччя.
Означення: Нульовою (основною) називається гіпотеза  , яку висувають. Конкуруючою (альтернативною) називається гіпотеза
, яку висувають. Конкуруючою (альтернативною) називається гіпотеза  , що вступає з нульовою гіпотезою в протиріччя.
, що вступає з нульовою гіпотезою в протиріччя.
Висунута гіпотеза може бути правильною і може бути хибною, тому виникає необхідність її перевірки. При цьому можуть бути допущені помилки двох родів. Помилка першого роду полягає в тому, що буде відкинуто правильну гіпотезу. Помилка другого роду – що буде прийнято хибну гіпотезу. Ймовірність зробити помилку другого роду прийнято позначати через  і її називають рівнем значущості. Найбільш часто рівень значущості приймають таким, що дорівнює 0,05 або 0,01. Якщо взяти рівень значущості, що дорівнює 0,01, тоді це означає що у 1 випадку із 100 є ризик припустити помилку першого роду, тобто відкинути правильну гіпотезу. При контролі якості продукції ймовірність вважати бракованою партію придатних товарів (помилка першого роду) називається “ризиком виробника”, а ймовірність прийняти браковану партію за придатну (помилка другого роду) – “ризиком споживача”.
і її називають рівнем значущості. Найбільш часто рівень значущості приймають таким, що дорівнює 0,05 або 0,01. Якщо взяти рівень значущості, що дорівнює 0,01, тоді це означає що у 1 випадку із 100 є ризик припустити помилку першого роду, тобто відкинути правильну гіпотезу. При контролі якості продукції ймовірність вважати бракованою партію придатних товарів (помилка першого роду) називається “ризиком виробника”, а ймовірність прийняти браковану партію за придатну (помилка другого роду) – “ризиком споживача”.
Для перевірки нульової гіпотези використовують спеціально підібрану випадкову величину, точне або наближене значення якої невідоме. Цю величину позначають великими літерами латинського алфавіту в залежності від розподілу, який вона має. Наприклад, якщо величина має нормальний розподіл, то її прийнято позначати або  або
або  ; якщо має розподіл Фішера-Снедекора, тоді
; якщо має розподіл Фішера-Снедекора, тоді  або
або  ; Ст’юдента -
; Ст’юдента -  ; “хі квадрат” Пірсона -
; “хі квадрат” Пірсона -  .
.
 Означення: Статистичним критерієм називається випадкова величина, що служить для перевірки нульової гіпотези. Спостережувальним значенням критерія називається значення випадкової величини, яке обчислене за вибірками.
Означення: Статистичним критерієм називається випадкова величина, що служить для перевірки нульової гіпотези. Спостережувальним значенням критерія називається значення випадкової величини, яке обчислене за вибірками.
 Приклад:
Приклад:
Якщо перевіряють гіпотезу про рівність дисперсій двох нормальних генеральних сукупностей, тоді за критерій приймають відношення вибіркових дисперсій  . Ця величина є випадковою, тому в різних дослідах дисперсії приймають різні, наперед невідомі значення, що розподіляються за законом Фішера-Снедекора. Якщо за двома вибірками знайдено виправлені вибіркові дисперсії
. Ця величина є випадковою, тому в різних дослідах дисперсії приймають різні, наперед невідомі значення, що розподіляються за законом Фішера-Снедекора. Якщо за двома вибірками знайдено виправлені вибіркові дисперсії  , тоді спостережувальне значення критерія
, тоді спостережувальне значення критерія  знаходиться, як
знаходиться, як 
Розділ 15.2. Критична область. Область приняття нульової гіпотези. Критична точка
Після вибору необхідного критерія, множину всіх його можливих значень розбивають на дві підмножини: одну, що вміщує значення критерія та другу, що його не вміщує.
 Означення: Критичною областю називається сукупність значень критерія, при яких нульову гіпотезу відкидають. Областю прийняття нульової гіпотези (областю припустимих значень) називається сукупність значень критерія, при яких гіпотезу приймають. Критичними точками (границями)
Означення: Критичною областю називається сукупність значень критерія, при яких нульову гіпотезу відкидають. Областю прийняття нульової гіпотези (областю припустимих значень) називається сукупність значень критерія, при яких гіпотезу приймають. Критичними точками (границями)  називаються точки, що відділяють критичну область від області прийняття гіпотези.
називаються точки, що відділяють критичну область від області прийняття гіпотези.
Розрізняють односторонню (односторонню і правосторонню) та двосторонню критичні області.
Означення: Правосторонньою називається критична область, що визначається нерівністю  , де
, де  - додатнє число. Лівосторонньою називається критична область, що визначається нерівністю
- додатнє число. Лівосторонньою називається критична область, що визначається нерівністю  , де
, де  - додатнє число. Двосторонньою називається критична область, що визначається нерівностями
- додатнє число. Двосторонньою називається критична область, що визначається нерівностями  , де
, де  .
.
Якщо критичні точки симетричні відносно нуля, то двосторонню критичну область можна задати нерівністю  .
.
 Відшукування правосторонньої критичної області
Відшукування правосторонньої критичної області
Для знаходження правосторонньої критичної області необхідно знайти критичну точку. Для цього задаються достатньо малою ймовірністю – рівнем значущості  і шукають критичну точку
і шукають критичну точку  , виходячи з вимоги, що при умові справедливості нульової гіпотези ймовірність того, що
, виходячи з вимоги, що при умові справедливості нульової гіпотези ймовірність того, що  повинна дорівнювати прийнятому рівню значущості
повинна дорівнювати прийнятому рівню значущості
 .
.
Для кожного критерія існують відповідні таблиці, за якими знаходять критичну точку, що задовольняє цій умові. Якщо критичну точку вже знайдено, тоді за даними вибірки обчислюють спостережувальне значення критерію. Якщо  , тоді нульову гіпотезу відкидають. Якщо
, тоді нульову гіпотезу відкидають. Якщо  , тоді немає підстав відкинути нульову гіпотезу.
, тоді немає підстав відкинути нульову гіпотезу.
 Відшукування лівосторонньої критичної області
Відшукування лівосторонньої критичної області
Для знаходження лівосторонньої критичної області необхідно знайти критичну точку. Для цього задаються достатньо малою ймовірністю – рівнем значущості  і шукають критичну точку
і шукають критичну точку  , виходячи з вимоги того, що при умові справедливості нульової гіпотези ймовірність того, що
, виходячи з вимоги того, що при умові справедливості нульової гіпотези ймовірність того, що  повинна дорівнювати прийнятому рівню значущості
повинна дорівнювати прийнятому рівню значущості
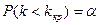 .
.
 Відшукування двосторонньої критичної області
Відшукування двосторонньої критичної області
Двосторонню критичну область знаходять виходячи з умови, що при справедливості нульової гіпотези сума ймовірностей того, що критерій прийме значення менше  або більше
або більше  , буде дорівнювати прийнятому рівню значущості
, буде дорівнювати прийнятому рівню значущості 
 .
.
Якщо критичні точки є симетричними, тоді


Поиск по сайту: