Определение закрытой модели ТЗ. Критерий существования решения ТЗ

Опр: Транспортная задача, для которой выполняется усл (1) наз. закрытой, в противном случае – открытой.

ТЕОРЕМА 1: Транспортная задача имеет решения тогда, и только тогда, когда (1)

(1) – наз.условием баланса.

Док-во. Необходимость. Пусть решение транспортной задачи сущ. ,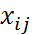

. ,

Достаточность. Пусть выполняется условие баланса (1) Построим след.план перевозок

,

Из условия следует, что множество планов является замкнутым. Кроме этого оно является ограниченным. Действительно, если возьмем любую перевозку. Целевая функция является линейной, следовательно и непрерывной. Отсюда по теореме Вейерштрасса решение задачи существует.

Замеч. Открытую ТЗ можно свести к закрытой след. обр:

1) если 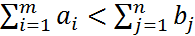, то вводим фиктивный пункт производства с запасами продукции в нем в кол-ве и нулевыми стоимостями перевозок из него.

2) Если то вводим фиктивный пункт потребления с потребностямипродукции в нем и нулевыми стоимостями перевозок в него.

Поиск по сайту: