Масса. Уравнение движения (2-й закон Ньютона)

В ньютоновской механике массой материальной точки называется положительная скалярная величина, являющаяся мерой инертности этой точки. Под действием силы материальная точка изменяет свою скорость не мгновенно, а постепенно, т. е. приобретает конечное ускорение, которое тем меньше, чем больше масса материальной точки, т. е. или 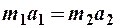. В системе СИ размерность .

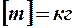В ньютоновской механике масса обладает следующими свойствами:

- масса материальной точки не зависит от состояния её движения и является величиной постоянной;

- масса - величина аддитивная, т. е. масса системы точек равна сумме масс всех точек этой системы;

- масса замкнутой системы остаётся величиной неизменной при любых процессах в этой системе (закон сохранения массы).

Плотностью тела в данной его точке М называется отношение массы малого элемента тела, включающего т. М, к величине объёма этого элемента: 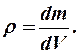Размеры элемента должны быть настолько малы, чтобы плотность в его пределах была величиной неизменной, но всё же эти раз­меры должны быть гораздо больше межмолекулярных расстояний вещества данного тела. В системе СИ размерность .

Тело называется однородным, если во всех его точках Тогда масса однородного тела при известной плотности будет равна 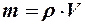. Если тело неоднородное, то массу ищем как интеграл по объёму: .

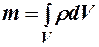Опыт показывает, что ускорение , приобретаемое материальной точкой под действием силы 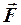, прямо пропорционально модулю этой силы и обратно пропорционально массе точки, причем направле­ние ускорения совпадает с линией действия силы, т. е. 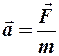. В системе СИ размерность .

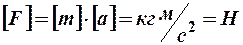Определяя ускорение как получим 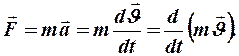Векторная величина, равная произведению массы точки на её скорость, т. е. 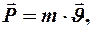называется импульсом материальной точки. В системе СИ размерность 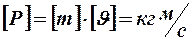Тогда предыдущее уравнение примет вид:

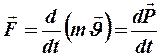. (1)

Уравнение (1) является выражением основного закона динамики материальной точки (второй за­кон Ньютона) и служит принципом причинности в классической механике. Этот закон позволяет при из­вестном начальном состоянии и действующей силе определить состояние материальной точки в произ­вольный момент времени .

Опыт показывает, что, если на материальную точку одновременно действуют несколько сил, то ка­ждая из них сообщает точке своё ускорение, как если бы других сил не было (принцип независимо­сти действия сил). Т. е. ускорение, приобретаемое материальной точкой под действием нескольких сил, будет где 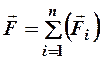- результирующая сила.

Подставив в уравнение (1) 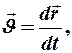получим:

. (2)

Дифференциальное уравнение (2) называют уравнением движения материальной точки. В проекциях на оси координат , , 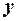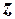это уравнение примет вид:

Поиск по сайту: