 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
МАТЕРИАЛОВЕДЕНИЕ
Учебное пособие
Часть 1 Магнитные материалы
Лабораторный практикум
Санкт-Петербург 2013
УДК 621. 315. 416
Учебное пособие. Киршина И.А., Наймитенко Н.В., Плотянская М.А.,Федченко В.Г. Материаловедение. Часть 1.
Исследование магнитных материалов. Лабораторный практикум / СПбГУАП. СПб.,
2013. 50 с.; ил.60, табл.6
Учебное пособие подготовлено на кафедре микро- и нанотехнологии аэрокосмического приборостроения университета аэрокосмического приборостроения и предназначен для студентов специальностей, связанных с радиоаппаратостроением, приборостроением и электронной техникой, при изучении дисциплин “Материалы и элементы электронной техники”, “Материаловедение”, “Химия и материаловедение”, ”Материаловедение и ТКМ”, а также для выполнения лабораторных работ и самостоятельной подготовки.
Содержание
1 Магнитные материалы 4
1.1 Основные магнитные характеристики. Классификация видов магнетизма 4
1.2 Природа ферромагнетизма. Доменная структура ферромагнетиков 5
1.3 Основная кривая намагничивания и предельный гистерезисный цикл.
Процесс технического намагничивания 11
1.4 Коэффициент размагничивания 16
1.5 Теория коэрцитивной силы ферромагнитных материалов с многодоменной структурой 18
1.6 Теория коэрцитивной силы ферромагнитных материалов с однодоменной структурой 21
1.7 Зависимость индукции насыщения и остаточной магнитной индукции 23
от химического состава и структуры материала
1.8 Магнитомягкие материалы для работы на низких частотах 27
1.9 Магнитомягкие материалы для работы на высоких частотах 31
1.10 Магнитотвердые материалы 35
2 Лабораторная работа №8. Исследование магнитотвердых материалов 40
3 Лабораторная работа №9. Исследование магнитомягких материалов 45
4 Лабораторная работа №10. Определение температуры Кюри магнитных
материалов 48
1 Магнитные материалы
1.1 Основные магнитные характеристики. Классификация видов магнетизма
Магнитное поле, как и электрическое, является формой существования материи. Оно проявляется в пространстве посредством возникновения магнитных сил, действующих только на движущиеся электрические заряды.
Ампер (1931г.) предположил, что каждый элементарный магнит представляет собой круговой ток, циркулирующий внутри частицы вещества (атома, молекулы и группы молекул).
Любой круговой ток можно охарактеризовать магнитным моментом, равным произведению силы электрического тока на площадь, охватываемую током.

Рисунок 1
Вектор магнитного момента (М) направлен по нормали к плоскости контура так, чтобы из конца вектора ток казался протекающим против часовой стрелки. Если магнитный момент создается каким-то веществом, то, разделив величину этого момента на объем образца, получим удельный магнитный момент J, который называется намагниченностью данного вещества

При внесении образца из исследуемого вещества во внешнее магнитное поле, величина намагниченности не остается постоянной, но изменяется в зависимости от напряженности внешнего магнитного поля. Коэффициент пропорциональности называют магнитной восприимчивостью.

По величине магнитной восприимчивости все вещества делятся на три группы: диамагнетики, парамагнетики и ферромагнетики.
Диамагнетиками называют вещества, восприимчивость которых отрицательна (они выталкиваются из неравномерного магнитного поля) и не зависит от напряженности магнитного поля.
Парамагнетиками называют вещества, магнитная восприимчивость которых больше нуля и не зависит от напряженности магнитного поля. Парамагнетики слабо втягиваются в неравномерное магнитное поле.
Ферромагнетики - вещества, для которых магнитная восприимчивость есть величина положительная и зависит от напряженности магнитного поля. Ферромагнетики сильно втягиваются в неравномерное магнитное поле.
Наряду с намагниченностью используется при технических расчетах такая характеристика, как индукция В. Если существует в каком-то пространстве магнитное поле, то индукция этого поля (плотность магнитного потока) связана с напряженностью магнитного поля

Коэффициентом пропорциональности в системе СИ является некоторая физическая константа µo - абсолютная магнитная проницаемость вакуума.
Если в некотором объеме существует еще и вещество, то индукция магнитного поля зависит не только от напряженности внешнего магнитного поля, но и от намагниченности вещества
 ,
,
где µ0= 4π· 10-7 (Тл).
Иногда эту же характеристику записывают, вводя дополнительную магнитную характеристику вещества µ – относительную магнитную проницаемость вещества
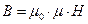
Величина эта безразмерная и показывает, во сколько раз увеличивается индукция магнитного поля в объеме, занятом веществом. По абсолютной величине относительная магнитная проницаемость близка к магнитной восприимчивости
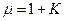
Если внести пробный магнит в поле, неравномерное в пределах его длины, то можно измерить силу, действующую на этот пробный магнит. Такое действие свидетельствует о том, что в разных точках магнитного поля действует разная напряженность магнитного поля. Напряженность Н – величина векторная. За положительное направление принимают направление действия поля на северный полюс магнита.
Поле, напряженность которого постоянна в разных точках по величине и направлению, называют однородным. Такое поле действует на оба полюса магнита с одинаковыми и противоположно направленными силами, образующими пару сил.
Напряженность поля длинной цилиндрической катушки, витки которой намотаны в виде спирали, представляет собой постоянную величину по оси соленоида и по форме силовых линий и их распределению не отличается от постоянного магнита.
Обычно напряженность поля для такой катушки

За единицу напряженности принимается напряженность поля такой катушки, что при намотке на 1м длины l по образующей цилиндра с числом витков N по виткам протекает ток I/N А.
1.2 Природа ферромагнетизма. Доменное строение ферромагнетиков
Все ферромагнетики делят на три группы: металлы железной группы, редкоземельные элементы и сплавы, которые состоят из немагнитных компонентов, но сами обладают ферромагнитными свойствами.
В первой группе три металла: железо, никель и кобальт, которые входят и во все ферромагнитные металлические сплавы, применяющиеся в технике. Находят применение они и в чистом виде.
Вторая группа включает шесть редкоземельных элементов: гадолиний, диспрозий, тербий, гольмий, эрбий и тулий.
К третьей группе ферромагнетиков принадлежат сплавы, которые составлены из неферромагнитных компонентов, но которые сами (в виде сплавов) проявляют ферромагнитные свойства. В технике известны сплавы на основе серебра, платины, висмута с ферромагнитными свойствами.
Магнетизм (и ферромагнетизм, частности) - это свойство движущегося электрического заряда. Можно предположить, что движение электронов в атоме будет создавать магнитные свойства вещества.
Электрон вращается вокруг ядра, поэтому естественно предположить, что именно орбитальное движение и создает магнитные свойства. Величина тока, движущегося по орбите электрона, может быть найдена как произведение заряда электрона на частоту вращения, при этом создается магнитный орбитальный момент электрона
 (1)
(1)
Механический момент движущегося по орбите электрона можно рассчитать по формуле

Он принимает только определенные квантовые значения (согласно теории Бора). Если учесть выражения для скорости (V=ω·r) и круговой частоты электрона (ω=2π·f), то уравнение можно переписать в виде равенства

При этом площадь электронной орбиты

Подставив это выражение в формулу для магнитного орбитального момента электрона, получим окончательную формулу

Из этого выражения ясно, что магнитный момент, как и механический, квантуется. Взяв квантовое число равным 1, получаем минимальный магнитный момент (квант магнитного момента). Этот квант назвали магнетоном Бора

Отношение магнитного момента к механическому называется гиромагнитным отношением

Если подставить в это отношение выражения для магнитного и механического моментов, получим постоянное число

Когда экспериментально определили гиромагнитное отношение, у ферромагнетиков результат оказался в два раза больше расчетного

Это не могло быть простой ошибкой. Умножим полученное экспериментально гиромагнитное отношение на величину магнетона Бора. При этом должен получиться механический момент

Величина этого момента оказывается пропорциональной постоянной Планка, точнее постоянной Ферми с коэффициентом пропорциональности равным ± 1/2

Этот коэффициент пропорциональности является четвертым квантовым числом электрона. Появляется оно потому, что электрон участвует еще в одном движении – спиновом (рисунок 2). Об этом говорит и магнитный момент ферромагнетика. Таким образом, можно сделать вывод, что магнитный момент ферромагнетиков имеет спиновую природу.
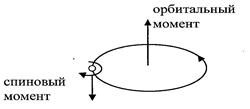
Рисунок 2 - Боровская модель атома
Рассмотрим строение электронной оболочки атома наиболее распространенного ферромагнетика - железа. Железо имеет заряд +26, поэтому вокруг ядра в атоме железа вращаются 26 электронов, которые заполняют соответствующие электронные оболочки (рисунок 3).
У железа 3d оболочка недостроена. Максимально на этой оболочке может содержаться 10 электронов. С учетом правила Хунда заполнение оболочки идет таким образом, что оболочку занимают сначала 5 электронов со спином одного направления, а потом один электрон с противоположным спином. Поэтому суммарный магнитный момент этой оболочки равен 4 магнетонам Бора.

Рисунок 3
Этот магнитный момент и составляет практически суммарный магнитный момент изолированного атома железа.
Магнитный момент изолированного атома кобальта равен 3 магнетонам Бора, а магнитный момент атома никеля – 2 магнетонам Бора. В кристаллической решетке в результате взаимодействия с соседними атомами каждый атом вносит меньший вклад в общий суммарный магнитный момент ферромагнетика.
Между двумя атомами, обладающими отличными от нуля магнитными моментами действуют особый вид взаимодействия – обменное (рисунок 4). При этом энергия обменного взаимодействия
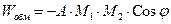 (2)
(2)
Величина коэффициента А зависит от отношения параметра кристаллической решетки к радиусу недостроенной электронной оболочки, которая и создает магнитный момент атома (рисунок 5).

Рисунок 4 Рисунок 5
На кривой можно выделить три участка. Второй участок соответствует ферромагнетизму. Энергия обменного взаимодействия имеет достаточно большую величину и знак минус, что говорит о том, что векторы магнитных моментов повернуты параллельно друг другу. При этом косинус угла равен 1. Действительно, система самопроизвольно стремится сохранить знак (-) перед энергией обменного взаимодействия, так как в этом случае энергия обменного взаимодействия вычитается из общего запаса свободной энергии системы. Любая система всегда стремится иметь минимальный запас свободной энергии. При положительном коэффициенте А сделать это можно только установлением такого угла между векторами магнитных моментов, чтобы косинус был равен +1. Энергия теплового колебательного движения стремится к беспорядочному расположению векторов, но так как абсолютная величина энергии обменного взаимодействия большая (больше энергии тепловых колебаний), то она удерживает векторы магнитных моментов параллельно друг другу. Третья область имеет малую величину коэффициента А, поэтому мала абсолютная величина энергии обменного взаимодействия, эта энергия не может удержать векторы магнитных моментов параллельно друг другу и векторы располагаются беспорядочно. Это соответствует парамагнетизму. Первая область имеет отрицательную величину коэффициента А, поэтому, чтобы сохранить в формуле для энергии знак минус, угол должен иметь величину 180°, т.е. векторы магнитных моментов атомов должны быть антипараллельны, что соответствует антиферромагнетизму.
Можно сформулировать два условия ферромагнетизма:
а) магнитные моменты атомов отличны от нуля;
б) если выполняются неравенства 3 ≤ a/r, то существует температура θ (температура Кюри), ниже которой |Wоб| > |Wтепл|.
Если вещество отвечает двум условиям ферромагнетизма, то магнитные моменты атомов расположены параллельно, а это означает, что вещество намагничено до насыщения и вокруг него должно существовать магнитное поле. В действительности такого поля нет (пока ферромагнетик не намагничен внешним магнитным полем). Это связано с тем, что ферромагнетики имеют доменное строение. Они разбиты на отдельные области (домены), в пределах которых все магнитные моменты атомов параллельны друг другу, т.е. отвечают двум условиям ферромагнетизма, но магнитные моменты доменов Js так ориентированы в пространстве, что при их суммировании получается нулевой магнитный момент и ферромагнетик кажется ненамагниченным. Внешнее магнитное поле у такой структуры практически равно нулю (рисунок 6).
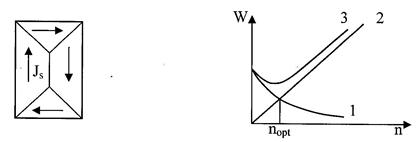
Рисунок 6 Рисунок 7
С появлением доменного строения изменяется энергия, запасенная во внешнем магнитном поле (магнитостатическая энергия). Чем больше число доменов, тем меньше эта магнитостатическая энергия (кривая 1 на рисунке 7). Практически при многодоменном строении остаются небольшие замыкающие магнитные поля между соседними доменами, которые можно обнаружить экспериментально с помощью достаточно точных измерений. С появлением многодоменного строения появляются и границы между доменами, на которые необходимо затрачивать определенную энергию. Энергия доменных стенок есть преимущественно энергия магнитной анизотропии (кривая 2 на рисунке 7). Суммируя эти оба вида энергии, получаем кривую 3 на рис.7, которая имеет минимум при определенном числе доменов. Поэтому система самопроизвольно делится на оптимальное число доменов.
Можно рассмотреть и строение границы между доменами. Если эту границу представить как некоторую условную линию между двумя соседними рядами атомов, то вектора магнитных моментов двух атомов, принадлежащих разным доменам, будут разориентированы на значительные углы (90 или 180°), поэтому величина энергии обменного взаимодействия между такими атомами будет значительной. Если же стенку представлять имеющей толщину из многих видов атомов, то поворот векторов магнитных моментов в пределах стенки будет происходить постепенно и энергия обменного взаимодействия будет тем меньше, чем меньше будет угол разориентации, т.е. чем толще будет доменная стенка (по аналогии с кривой 1 на рисунке 7).
С другой стороны, в пределах каждого магнитного домена векторы магнитных доменов развернуты в направлениях легкого намагничивания. Это происходит самопроизвольно без нашего участия.
Речь в данном случае идет о том, что намагничивание материала есть анизотропное свойство. Если попытаться намагничивать монокристалл в разных направлениях, то энергия, затрачиваемая на процесс намагничивания (заштрихованная область на рисунке 8), будет разной.

Рисунок 8
Можно найти направление, по которому намагнитить ферромагнетик легче всего, это направление называют направлением легкого намагничивания (НЛН) и можно найти направление, по которому намагничивать труднее всего, это - направление трудного намагничивания (НТН). Энергия, заключенная между этими крайними кривыми, называется энергией магнитной анизотропии. Когда в пределах доменной стенки векторы магнитных моментов доменов поворачиваются из одного НЛН в другое, то они находятся в НТН, поэтому доменная стенка обладает повышенным запасом энергии, которая по своей природе есть энергия магнитной анизотропии (кривая 2 на рисунке 7). Просуммировав обе кривые, получаем зависимость (3), которая имеет минимум. Система всегда стремится занять положение с минимальным запасом свободной энергии, поэтому устанавливается оптимальная толщина доменных стенок. Примеры кристаллических решеток и направлений намагничивания приведены на рисунке 9.

Рисунок 9 - Кристаллические решетки и направления намагничивания
Заканчивая рассмотрение данного вопроса, следует отметить, что кроме названных видов энергии при намагничивании существуют и другие виды энергий

В общем случае система стремится к минимальному значению этой суммы, так как она входит в общий запас свободной энергии системы. Когда намагничивается какой-либо образец ферромагнетика, то наряду с изменением магнитного состояния, он меняет и размеры (удлиняется или укорачивается). Это явление называют магнитострикцией и оценивают величиной относительного удлинения образца

Так как намагничивание может быть у образца разным, то условились сравнивать различные ферромагнетики по коэффициенту магнитострикции, измеряя этот коэффициент в состоянии насыщения (λs). Коэффициент магнитострикции может быть положительным и отрицательным. При намагничивании многодоменного ферромагнетика происходит перемагничивание каждого домена, поэтому каждый домен изменяет свои размеры поразному и внутри материала создаются внутренние напряжения, которые следует преодолеть в процессе намагничивания. На это требуется затратить некоторую энергию, которая называется энергией магнитострикции насыщения (Wλ). Магнитостатическая энергия (Wo) представляет собой энергию, запасенную во внешнем магнитном поле домена. С уменьшением размера домена, уменьшается величина Js2 и, следовательно -Wo.
Энергия магнитного взаимодействия Wм определяет энергию взаимодействия внешнего намагничивающего поля (Н) и поля домена Js. Формула для расчета этой энергии напоминает формулу для энергии обменного взаимодействия




Если при больших размерах образца ферромагнетики самопроизвольно стремятся к многодоменному строению, то в процессе дробления ферромагнетика можно получить малую по размерам частицу, для которой однодоменное состояние оказывается более предпочтительным, чем многодоменное, так как энергия, запасенная во внешнем поле, будет меньше энергии запасенной в доменной стенке. Любой ферромагнетик можно перевести в однодоменное состояние.
1.3 Основная кривая намагничивания и предельный гистерезисный цикл
Для построения основной кривой намагничивания можно использовать замкнутый образец из ферромагнетика с намагничивающей обмоткой, как это показано на рисунке 10, и, если через его обмотку пропускать намагничивающий ток, магнитное состояние образца будет меняться. Исходное состояние соответствует точке 0 на кривой зависимости B= φ(Н) (рисунок 11).

Рисунок 10 Рисунок 11
По мере увеличения тока растет индукция в образце по кривой 0a. Индукция в точке а называется индукцией насыщения (Bs). Это самая большая индукция, которая может быть получена у данного вещества. Если продолжать намагничивание, то индукция будет расти в данном объеме пространства и выше точки а, пропорционально увеличению напряженности намагничивающего поля, однако, образец ферромагнетика на величину этой индукции уже не будет оказывать никакого влияния, а рост индукции будет пропорционален росту напряженности намагничивающего поля с коэффициентом пропорциональности µo. Если размагничивать образец ферромагнетика после того как его намагнитили до насыщения и выше, то до точки a размагничивание будет происходить по той же кривой, что и намагничивание, а начиная с точки а, кривая размагничивания (кривая аb) не будет совпадать с кривой намагничивания. Если уменьшить намагничивающий ток до нуля, после намагничивания образца до насыщения, то попадем в точку b. Можно изменить направление намагничивающего тока и начать намагничивание в противоположном направлении. В результате достигнем точки c, а затем d, при этом образец окажется перемагничен до насыщения в противоположном направлении по сравнению с точкой а. Наконец, меняя еще раз направление тока можно опять вернуться в точку а, замкнув кривую аbcdef, которая называется предельным гистерезисным циклом. Таким образом, в процессе перемагничивания образца получают две кривые: основную кривую намагничивания 0a и предельный гистерезисный цикл аbcdef.
По этим двум кривым можно определить несколько важных магнитных характеристик ферромагнетика. Первая - индукция насыщения (Bs) (см. выше). Вторая характеристика представляет собой индукцию остаточную (Br). Это индукция, которая остается в предварительно намагниченном до насыщения замкнутом кольцевом образце при уменьшении напряженности намагничивающего поля до нуля.
Третья характеристика - коэрцитивная сила Нc. Коэрцитивной силой называют напряженность намагничивающего поля, взятую с обратным знаком, которую надо приложить к предварительно намагниченному до насыщения замкнутому кольцевому образцу, чтобы уменьшить индукцию в образце до нуля.
По основной кривой намагничивания можно определить относительную магнитную проницаемость

Таким образом, µ пропорциональна тангенсу угла наклона секущей, проведенной через начало координат и точку, в которой определяется проницаемость. Коэффициент пропорциональности m зависит от выбранных масштабов по осям.
Если точка скользит по кривой к началу координат, то тангенс угла уменьшается и уменьшается относительная магнитная проницаемость. При определении проницаемости вблизи точки 0, мы получаем характеристику µн, которую называют начальной магнитной проницаемостью. Эта характеристика приводится в справочниках и является важной при работе ферромагнетика в слабых магнитных полях. Если точка скользит вдоль основной кривой намагничивания вверх по направлению к точке а, то на изгибе основной кривой намагничивания секущая превращается в касательную к основной кривой намагничивания, а угол наклона этой касательной и тангенс угла будут максимальными. Пропорционально максимальному тангенсу получаем максимальную относительную магнитную проницаемость µmax, которая важна для материалов, работающих в сильных магнитных полях.
На рисунке 12 приведена типичная зависимость относительной магнитной проницаемости ферромагнетика от напряженности магнитного поля, на которой отмечены обе магнитные характеристики

Рисунок 12
По предельному гистерезисному циклу можно определить также потери в ферромагнетике. Потери в ферромагнетике складываются из двух видов потерь: на гистерезис и на вихревые токи
 (3)
(3)
 (4)
(4)
Если перемагничивание производить медленно, то площадь гистерезисного цикла будет пропорциональна потерям на гистерезис. Если же направление тока намагничивания менять быстро, то в сердечнике магнитопровода возникают вихревые токи, которые вызывают появление потерь на вихревые токи. Площадь гистерезисного цикла растет, а сам цикл меняет при этом свою форму, приближаясь к эллипсу.
На предельном гистерезисном цикле работают редко, гораздо чаще на цикле, лежащем внутри предельного, который называется рабочим гистерезисным циклом.
По формуле 3 рассчитывают потери на гистерезис рабочего гистерезисного цикла за единицу времени. Эти потери зависят от коэрцитивной силы рабочего цикла (Н'c), максимальной индукции (Вm) и частоты перемагничивания. Коэффициент α учитывает форму гистерезисного цикла.
Потери на вихревые токи рассчитывают по формуле 4, в которую входят уже известные величины, а также отношение квадрата толщины листа магнитопровода (d) к удельному электрическому сопротивлению материала магнитопровода (ρ).
Из формулы ясно, что для того, чтобы уменьшить потери на вихревые токи в трансформаторе, необходимо набирать пакет магнитопровода трансформатора из тонких пластин ферромагнитного материала, изолированных электрически друг от друга, а не делать сплошным. Материал должен иметь высокое ρ, что достигается легированием.
Рассмотрим характер изменения доменной структуры ферромагнетика при намагничивании.
Энергия взаимодействия магнитного домена с внешним намагничивающим полем находится по формуле 5
 (5)
(5)
Это энергия, которую в предыдущей теме назвали энергией магнитного взаимодействия. При этом взаимодействуют два магнитных поля: внешнее и поле магнитного домена.
В процессе намагничивания нет необходимости знать абсолютную величину энергии магнитного взаимодействия. Достаточно знать изменение этой энергии в процессе намагничивания (перемагничивания). Для этого необходимо условиться в начальном уровне отсчета энергии. Удобнее начать отсчет от состояния, когда направления векторов намагничивания магнитных доменов Js совпадают с направлением внешнего намагничивающего поля (φ=0)

Тогда изменение энергии в процессе перемагничивания

На рисунке 13 показана граница двух доменов 1 и 2, которая подвергается действию намагничивающего поля Н (направление поля показано стрелкой). При взаимодействии намагничивающего поля с полем первого домена энергия системы не изменяется (∆W1=0), а со вторым доменом увеличивается (∆W2=2µ0JsH). Это увеличение невыгодно системе, поэтому она отреагирует таким образом, чтобы уменьшить это увеличение, передвинув стенку между доменами в сторону второго домена. При этом первый домен будет расти в объеме, а второй - уменьшаться.

Рисунок 13 Рисунок 14
На рисунке 14 показана стенка между доменами при своем движении. Пусть стенка в положении X имеет определенный запас поверхностной удельной энергии стенки γ. Если она передвинется на некоторую величину, то произойдет и изменение поверхностной энергии стенки (γ + dγ), так как энергия стенки зависит от ее положения в ферромагнетике. Выигрыш равен энергии намагничивания части объема второго домена в результате движения стенки, а проигрыш, который уравновешивает этот выигрыш, равен суммарной изменившейся энергии стенки

Преобразуя это равенство, можно написать уравнение, которое называют уравнением движения доменной стенки

На рисунке 15 показан характер изменения градиента энергии доменной стенки от величины X.
В исходном состоянии стенка находится в положении Х₀. Если из этого исходного положения сместить стенку внешним магнитным полем в положение X₁, то при выключении внешнего поля стенка сама вернется в положение Х₀, т.е. такое смещение будет обратимым (остаточная намагниченность отсутствует). Если полем сместить стенку в положение Х₂, то из этого положения стенка сама без приложения энергии извне перейдет в положение X₄. Если в положении Х₄ выключить внешнее поле, то стенка скатится в ближайшую потенциальную яму (положение Х₃), но не вернется в исходное состояние X₀, появится остаточная намагниченность.

Рисунок 15
На рисунке 16 показана кривая намагничивания, где можно выделить участки I и II. На участке 1а происходит упругое смещение стенок между доменами из исходного положения. Участок этот называется зоной Релея. Здесь отсутствует гистерезис. На участке 1б происходит скачкообразное перемещение границы между доменами. Скачки называют скачками Варкгаузена. Для этого участка характерна остаточная намагниченность и гистерезисный цикл. Зона I - это зона намагничивания за счет смещения доменной стенки. Зона II представляет зону с иным механизмом намагничивания. Здесь происходит поворот вектора магнитного момента. Изменение доменной структуры при этом показано на рисунке 16.
Когда поле отсутствует, ферромагнетик имеет исходную доменную структуру. С появлением внешнего намагничивающего поля начинают расти домены, векторы намагниченности которых, благоприятно ориентированы относительно направления вектора напряженности внешнего поля, но многодоменное строение при этом еще сохраняется. Если намагничивающей поле продолжает увеличиваться, то наступает момент, когда неблагоприятно ориентированные домены практически исчезают и весь образец ферромагнетика превращается в один домен (если образец представляет собой монокристалл). Если образец поликристаллический, то однодоменным становится каждое зерно этого поликристаллического образца. Это состояние соответствует окончанию первого участка на кривой намагничивания.

Рисунок 16 - Основная кривая намагничивания и изменение доменной структуры ферромагнетика при изменении напряженности магнитного поля
Дальнейшее намагничивание продолжается за счет поворота вектора магнитного момента до тех пор, пока этот вектор не будет параллельным вектору напряженности намагничивающего поля. Такое состояние соответствует режиму насыщения. Если теперь выключить внешнее намагничивающее поле, то новые домены в образце не появятся, но вектор магнитного момента из направления параллельного вектору Н, вернется в ближайшее направление легкою намагничивания.
1.4 Коэффициент размагничивани я
В предыдущей теме было рассмотрено поведение замкнутого тороидального ферромагнитного образца в магнитном поле. Если же образец разомкнутый (например, стержень на рисунке 17), то поведение образца будет другим. Намагничиваясь в поле, образец создает магнитные полюса и образует свое собственное магнитное поле, которое называют размагничивающим полем полюсов. Напряженность этого поля пропорциональна намагниченности

Коэффициент пропорциональности N называют коэффициентом размагничивания. Он зависит от формы образца. Чем длиннее стержень, тем дальше полюса магнита разнесены в пространстве, тем меньше коэффициент размагничивания (рисунок 18), и наоборот. Таким образом: разомкнутый ферромагнитный образец в магнитном поле находится одновременно под действием двух полей: внешнего поля Н и размагничивающего поля полюсов Hp, которые направлены навстречу друг другу.
Для того чтобы определить действительное магнитное состояние такого образца, возьмем основную кривую намагничивания для материала, из которого изготовлен такой образец и которая получена для замкнутого кольцевого образца (рисунок 19). Отложим напряженность намагничивающего поля Н, при этом, если бы образец был кольцевым, то для определения индукции достаточно восстановить перпендикуляр из точки А. Для разомкнутого образца надо еще отложить из точки А размагничивающее поле полюсов и только потом восстановить перпендикуляр. Координата точки d и определит действительную индукцию в образце Bd. Затруднение заключается в том, что неизвестна напряженность размагничивающего поля полюсов. Построим прямоугольный треугольник Adm.

Рисунок 17 Рисунок 18 Рисунок 19
Для точки d индукцию можно найти по формулам 6 и 7
 (6)
(6)
 (7)
(7)
Из уравнения 6 находим намагниченность в точке d
 (8)
(8)
Из уравнения 7 - относительную магнитную проницаемость в точке d, которая всегда больше 1

Поэтому уравнение 8 приобретает вид

Из треугольника Adm находим выражение
 ,
,
Отсюда

С учетом этой формулы всегда можно найти действительное магнитное состояние материала (точку d) простым построением. Откладываем напряженность внешнего намагничивающего поля» находим угол размагничивания, проводим луч из точки А под углом размагничивания до пересечения с основной кривой намагничивания. Наличие воздушного зазора делает кривую намагничивания более пологой (пунктирная линия на рисунке 19).
Особенно большую роль играет воздушный зазор в работе постоянных магнитов, которые обязательно делают с воздушным зазором.
Чтобы получить постоянный магнит, его предварительно намагничивают до насыщения, а затем убирают намагничивающее поле и работа магнита происходит за счет остаточного намагничивания. Если бы магнит был изготовлен в виде замкнутого образца, то его магнитное состояние можно было бы описать кривой размагничивания и такой характеристикой как остаточная индукция Вr. При наличии воздушного зазора найдем угол размагничивания, если известен для данной формы образца коэффициент размагничивания N. Построив угол размагничивания, как это показано на рисунке 20, найдем точку d, координаты которой и определяют действительную индукцию в образце Bd и действительную напряженность магнитного поля Нd. Напряженность магнитного поля Ho в воздушном зазоре пропорциональна величине Hd
 ,
,
гдe ld и l0 - длина магнита и воздушного зазора соответственно.

Рисунок 20
Энергия, которую отдает единица объема магнитного материала в воздушном зазоре (энергия магнитного поля) определяется по формуле

С изменением угла размагничивания эта энергия изменяется по кривой с максимумом (рисунок 20).
Максимальная энергия соответствует оптимальному углу размагничивания. Поэтому каждый материал должен быть при изготовлении магнита воплощен в такую форму, чтобы она соответствовала оптимальному углу размагничивания. В справочниках эта очень важная характеристика магнитных материалов указывается в одном из трех вариантов: Wmax, (Bd·Hd/2)max, (Bd·Hd)max.
1.5 Теория коэрцитивной силы ферромагнитных материалов с многодоменной структурой
Если намагнитить ферромагнетик с многодоменной структурой до насыщения, а потом убрать намагничивающее поле, то по кривой размагничивания попадем в точку Вr (рисунок 21). Чтобы попасть по этой кривой в точку Нc необходимо приложить определенной величины поле обратного направления по сравнению с намагничивающим полем. При этом произойдет размагничивание материала до такого состояния, что с учетом этого внешнего размагничивающего поля индукция станет равной нулю.

Рисунок 21
По какому же механизму идет размагничивание? Состояние в точке Вr характеризовалось тем, что кристалл представлял собой один домен, а вектор намагниченности вернулся из положения параллельного вектору напряженности магнитного поля, в ближайшее направление легкого намагничивания.
При приложении поля обратного знака можно было бы предположить, что перемещение по кривой размагничивания должно происходить за счет поворота вектора намагниченности внешним полем, а не за счет движения доменных стенок, которых в материале просто нет.
В действительности все происходит наоборот. Оказывается, что в материале всегда (даже в состоянии режима насыщения) остаются так называемые "антифазные домены", т.е. домены неблагоприятно ориентированные относительно намагничивающего поля. Теперь, когда мы прикладываем поле противоположного направления, эти "антифазные домены" начинают расти. Поэтому размагничивание происходит по механизму смещения доменных стенок.
Уравнение движения доменной стенки было получено ранее. Единственное уточнение, которое следует в этом уравнении сделать - перейти от текущего значения напряженности поля к его максимальному значению (коэрцитивной силе), а следовательно, и к максимальному градиенту
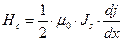 (9)
(9)
Существующие теории коэрцитивной силы различаются между собой смыслом, который они вкладывают в понятие удельной магнитной энергии доменной стенки γ.
Первая теория называется теорией внутренних напряжений. Согласно этой теории при смещении доменной стенки, векторы магнитных моментов выходят из положения легкого намагничивания, занимая различные другие положения. Это сопровождается магнитострикцией, т.е. деформацией ферромагнетика, на что требуется энергия. Удельную поверхностную энергию стенки можно представить в виде произведения объемной удельной энергии на толщину стенки

Удельную объемную энергию магнитострикции можно найти по формуле

Подставив эти выражения в уравнение 9, и проведя ряд упрощений, получим уравнение
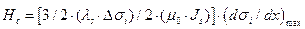
Теперь в данной формуле имеем градиент внутренних напряжений. Характер изменения σi по координате х показан на рисунке 22
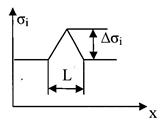
Рисунок 22
Это можно выразить в виде уравнения

Вводим коэффициент р (p=δ/l) и получаем окончательную формулу
 (10)
(10)
Экспериментальная проверка полученного уравнения показала, что иногда теоретические расчеты не совпадают с экспериментальными результатами, поэтому в дальнейшем была создана еще одна теория, теория немагнитных включений. Она предполагает, что внутри ферромагнетика всегда имеются немагнитные включения (раковины, поры, трещины, включения немагнитных фаз).
Стенка, перемещаясь по ферромагнетику, попадает на включения, и в той части стенки, которая приходится на включение (незаштрихованные участки) отсутствуют векторы магнитных моментов атомов» поэтому стенка уменьшает свою энергию. Чтобы "сдернуть" эту стенку с включения, необходимо совершить работу.
Рассмотрим плоскую картину, изображенную на рисунке 23

Рисунок 23
Энергия магнитного поля, двигающая доменную стенку, записана в левой части уравнения, а энергия, затрачиваемая на изменение энергии стенки - в правой
 (11)
(11)
Под энергией доменной стенки здесь понимается энергия магнитной анизотропии
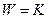 ;
; 
Считаем включения малыми по размерам
 ;
;  ;
;  ;
; 
Максимальная площадь, на которую изменяется площадь, занимаемая стенкой
 ,
,
а градиент этой площади

Подставляем полученный результат в уравнение 11, умножаем и делим все на диаметр включения и, вводя соответствующие коэффициенты, получаем окончательный результат
 (12)
(12)
Уравнение 12 имеет такую же сходимость с экспериментальными измерениями, как и уравнение 10, поэтому в дальнейшем их стали объединять в одно
 (13)
(13)
Это объясняется тем, что обе рассматриваемые в двух теориях причины имеют место. В материалах всегда имеются немагнитные включения, вокруг которых, главным образом, и распространяются зоны внутренних напряжений.
При создании ферромагнетиков обычно приходится решать две задачи: получить очень малую Нc у магнитомягких материалов магнитопроводов и получить высокую Нc у магнитотвердых материалов постоянных магнитов. Для получения очень малой коэрцитивной силы необходимо все величины, стоящие в числителе формулы 10, уменьшать, а стоящие в знаменателе - увеличивать. Для этого необходимо подбирать такой химический состав сплава, чтобы λs и К для него были близки к нулю. Уровень внутренних напряжений Δσi следует сделать возможно меньшим. Достигается это проведением рекристаллизационного отжига на конечной стадии технологического процесса изготовления пластин для любого магнитопровода.
Объемная доля немагнитных включений (а) должна быть как можно меньше, т.е. материал должен быть чистым и не содержать посторонних примесей. Если же включения все же полностью убрать не удается, то они должны так располагаться относительно будущих направлений движения доменных стенок при намагничивании, чтобы оказывать возможно меньшее сопротивление (малый коэффициент Р).
Намагниченность насыщения Js должна быть по возможности большой, что можно получить только у сплавов с большим содержанием атомов железа, так как именно эти атомы имеют максимальный магнитный момент.
При решении второй задачи требования обратные. Задача решается подбором химического состава сплава и созданием максимально возможного уровня внутренних напряжений. Такой уровень можно получить применением жесткой закалкой и мягкого отпуска, который делается только для того, чтобы эти внутренние напряжения не превышали предела прочности материала. Расчеты показывают, что даже если взять одну из наиболее прочных сталей и создать напряжения, близкие к пределу прочности, то и тогда но удается получить коэрцитивную силу больше 40 кА/м. Такой предел был достигнут на кобальтовых сталях еще в 30-х годах, которые практически исчерпали возможности многодоменных ферромагнетиков. Дальнейшее совершенствование материалов для постоянных магнитов связано с однодоменными ферромагнетиками.
1.6 Теория коэрцитивной силы ферромагнетиков с однодоменной структурой
Структура однодоменного ферромагнетика показана на рисунке 24. Здесь кружками отмечены не атомы, а однодоменные частицы, изолированные друг от друга немагнитной связкой.

Рисунок 24 Рисунок 25
Когда ферромагнетик намагничен до насыщения, то векторы намагниченности доменов повернуты в одну сторону и параллельны. Чтобы размагнитить такой магнит, надо у половины однодоменных частиц повернуть векторы намагниченности в одну сторону на 90°, а оставшейся половины - на 90° в другую сторону. При этом необходимо затратить определенную энергию, которую можно рассчитать по формуле

Так как φ=π/2, то формула преобразуется

Такому повороту препятствует энергия магнитной анизотропии

Тогда величина коэрцитивной силы

Величина коэффициента a зависит от типа кристаллической решетки и колеблется от 1 до 2. Формула справедлива, если однодоменные частицы имеют сферическую форму. Если же частицы вытянуты, то наряду с кристаллической анизотропией появляется еще изотропия формы частицы. На рисунке 25 показана одна частица вытянутой формы. Поскольку это однодоменная частица, то вокруг существует магнитное поле. Энергия, запасенная во внешнем магнитном поле
 (14)
(14)
Напряженность размагничивающего поля
 ,
,
а индукция
 ,
,
при этом напряженность внешнего намагничивающего поля Н следует приравнять нулю.
Подставив эти уравнения в 14, получаем равенство
 (15)
(15)
Величина коэффициента а'' зависит от количества однодоменных частиц. Для одной частицы коэффициент равен 0,5. Если частиц много и они влияют друг на друга, то a" =1. Вектор намагниченности частицы может быть направлен как по размеру а, так и по размеру b. Энергию магнитного поля в этих случаях рассчитывается по формуле 15. Самопроизвольно вектор установится по размеру b, так как коэффициент размагничивания
в этом случае будет меньше (полюса дальше отстоят друг от друга).
Внешним магнитным полем можно повернуть вектор намагниченности на 90˚ в направлении размера а. При этом придется затратить дополнительную энергию

Эта дополнительная энергия суммируется с энергией магнитной анизотропией и общее изменение энергии следует находить по формуле

В результате величину коэрцитивной силы можно вычислить по формуле

Она зависит как от обычной кристаллической анизотропии, так и от анизотропии, формы частиц. Если делать частицы сферическими, то практически можно получить величину коэрцитивной силы в 40 кА/м. Если использовать еще и анизотропию формы, то для вытянутых частиц можно эту цифру увеличить в несколько раз. В настоящее время постоянные магниты изготавливают преимущественно из однодоменных ферромагнетиков.
1.7 Зависимость индукции насыщения и остаточной индукции от химического состава и структуры материала
Предпоследняя электронная оболочка атома железа заполнена электронами не полностью. Нескомпенсированными оказываются 4 магнетона Бора. Если атом железа находится в кристаллической решетке, то из-за взаимодействия с соседними атомами суммарный вклад каждого атома в общий магнитный момент домена уменьшается до 2,16 Мб. У кобальта и никеля на предпоследней электронной оболочке меньше некомпенсированных электронов - 3 и 2 соответственно. Поэтому и вклад каждого атома в общий суммарный момент домена меньше (1,88/Мб и 0,66 /Мб). Это справедливо при температуре абсолютного нуля. Индукция насыщения у материала пропорциональна величине нескомпенсированного магнитного момента атома (таблица 1).
Если температура увеличивается, то беспорядок в расположении магнитных моментов увеличивается, а индукция насыщения уменьшается. Особенно это интенсивно происходит вблизи точки Кюри (рисунок 26). В таблице 1 указана температура Кюри для трех чистых ферромагнитных материалов
Таблица 1
| Bs,Тл | Θ, °С | |
| Fe | 2,16 | |
| Со | 1,88 | |
| Ni | 0,66 |

Рисунок 26
Добавление к любому из ферромагнетиков (Ф.М.) неферромагнитного материала (Н.Ф.М.) приводит к снижению индукции насыщения и точки Кюри. Можно так сильно разбавить ферромагнетик атомами, не имеющими магнитного момента, что исчезнет обменное взаимодействие и ферромагнетик превратится в парамагнетик (рисунок 27).
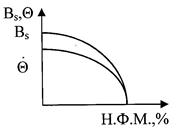
Рисунок 27
Сплавление ферромагнитных металлов между собой и значения индукции насыщения у сплавов показано на рисунке 28. Только в системе железо-кобальт при содержании кобальта от 35 до 50% индукция насыщения у сплавов больше, чем у чистого железа и достигает 2,42 Тл (рисунок 28, в).

Рисунок 28
Сплавы такого состава (их несколько) выделены в особую группу сплавов с высокой индукцией насыщения. Применяют эти сплавы (К50, Ф2, К35Х) для изготовления концентраторов магнитного потока и мембран телефонных аппаратов.
Остаточная индукция в основном зависит от структуры материала. На рисунке 29,a показан нетекстурованный поликристаллический ферромагнетик. Каждое зерно - это отдельный кристалл. Стрелками показаны возможные направления легкого намагничивания, по которым направлены векторы магнитных моментов доменов.
Если просуммировать все векторы магнитных моментов доменов, направив их из одной точки (рисунок 29,б) то в сумме получим 0. В состоянии насыщения все векторы будут параллельны вектору напряженности намагничивающего поля (рисунок 29,в). Если выключить поле, то в каждом зерне векторы из положения, в котором они оказались при насыщении, вернутся в ближайшее направление легкого намагничивания (рисунок 30). Положение кривых намагничивания и размагничивания показано на рисунке 31. При этом величина остаточной индукции примерно равна половине индукции насыщения.
В технике применяют текстурованные и нетекстурованные материалы. Нетекстурованные - изотропны (они одинаково намагничиваются во всех направлениях). Текстурованные имеют преимущественные направления легкого и трудного намагничивания, что свойственно монокристаллам, то есть текстурованный поликристаллический образец - анизотропен.
Наиболее часто в технике применяют продольную кристаллографическую текстуру. Её получают у деформируемых (пластичных) материалов с помощью прокатки с большими степенями деформации и рекристаллизационного отжига.

Рисунок 29

Рисунок 30 Рисунок 31
При прокатке зерна поликристалла дробятся на отдельные осколки, которые поворачиваются направлениями наибольшей прочности по направлению прокатки (Н.П.). С этим направлением, как правило, совпадает и направление легкого намагничивания (рисунок 32). Положение векторов намагничивания при отсутствии намагничивающего поля и при насыщении показаны на рисунке 33. Если в состоянии насыщения выключить намагничивающее поле, то вектор должен вернуться в ближайшее направление легкого намагничивания, в котором он уже находится. Поэтому индукция остается равной индукции насыщения (рисунок 34), а гистерезисный цикл становится прямоугольным (рисунок 35)

Рисунок 32 Рисунок 33 Рисунок 34 Рисунок 35
В некоторых материалах получают поперечную текстуру при прокатке (рисунок 36,а- направления легкого намагничивания направлены перпендикулярно Н.П.). Положение векторов магнитных моментов доменов показаны на рисунке 36 б,в,г. Теоретически в этом случае остаточная индукция равна нулю, а гистерезисный цикл называется линейным или перминварным. Реально остаточная индукция составляет несколько процентов от индукции насыщения (рисунок 37).

Рисунок 36 Рисунок 37
Для хрупких материалов используют еще один способ создания текстуры - направленную кристаллизацию. На рисунке 38 показана установка для направленной кристаллизации. Она состоит из тигля (огнеупорного стакана, в котором содержится расплавленный металл) и нагревательной электрической печи. Дно тигля полое и может охлаждаться водой.
Процесс кристаллизации начинается от дна тигля. При этом тигель опускается, выходя из нагревательной печи, поэтому фронт кристаллизации перемещается от дна тигля к поверхности металла. Кристаллизация заканчивается, когда фронт кристаллизации достигает поверхности.
На рисунке 39 показан начальный этап кристаллизации, когда появились только первые кристаллы. Они ориентированы произвольно относительно нормали к фронту кристаллизации. Скорость роста кристаллов анизотропна, как и любое другое свойство. Поэтому быстрее растут благоприятно ориентированные зародыши. Причем это направление совпадает и с направлением легкого намагничивания. Когда кристаллизация заканчивается, нижнюю часть слитка отрезают, а оставшуюся часть, состоящую из столбчатых кристаллов, используют как текстурованный ферромагнетик (рисунок 40).

Рисунок 38 Рисунок 39 Рисунок 40
Есть еще один способ создания текстуры - термомагнитная обработка. Делается эта обработка сразу на готовых магнитопроводах (рисунок 41). Обработке подвергаются только сплавы, состоящие из двух сортов атомов - магнитоактивных (с отличным от нуля магнитным моментом) и немагнитоактивных. К тому же материал должен иметь высокую точку Кюри. Обработка происходит таким образом: готовые сердечники устанавливают в приспособление, помещают в печь, нагревают до температуры несколько выше точки Кюри, включают магнитное поле и начинают медленно охлаждать. До включения поля магнитоактивные атомы располагались в кристаллической решетке совершенно хаотично (рисунок 42). Когда сердечник будет находиться при температуре ниже точки Кюри, под действием намагничивающего поля магнитоактивные атомы расположатся вдоль магнитных силовых линий, образуя цепочки атомов (рисунок 43).
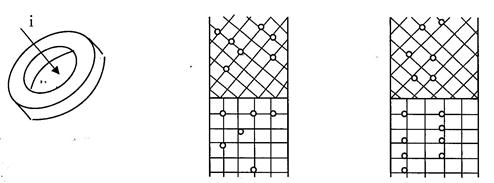
Рисунок 41 Рисунок 42 Рисунок 43
Такие цепочки образуют дополнительное направление легкого намагничивания к тем направлениям, которые существуют в кристаллической решетке. Если производить перемагничивание вдоль этих новых (наведенных) НЛН, то получается также прямоугольный гистерезисный цикл. Для ферритовых сердечников это очень распространенный способ получения прямоугольного гистерезисного цикла.
8 Магнитомягкие материалы для работы на низких частотах
Сформулируем требования для работы магнитомягких материалов на примере работы трансформатора. На рисунке 44 показана простейшая схема трансформатора.

Рисунок 44
Пусть на первичную обмотку трансформатора подается переменное напряжение, тогда напряжение на вторичной обмотке трансформатора определяется числом витков вторичной обмотки (W), площадью поперечного сечения магнитопровода (S) и скоростью изменения индукции в магнитопроводе (dB/dt). Полагая для простоты коэффициент трансформации равным 1, можно определить закон изменения индукции в магнитопроводе
 ,
,
дифференцируя, находим закон изменения индукции в магнитопроводе во времени
 ,
,
перед знаком синуса в этом уравнении стоит амплитудное значение индукции в магнитопроводе. Раскрывая круговую частоту через циклическую, находим выражение для действующего значения напряжения на обмотке трансформатора
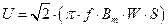

Поиск по сайту: