Условия существования экстремума для функции двух переменных

Необходимое: Если функция 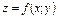достигает экстремума при х=х₀, у=у₀, то каждая частная производная первого порядка от этой функции при этих значениях аргументов или обращается в ноль или не существует.

Достаточное: Пусть в некоторой окрестности точки М₀(х₀,у₀) функция 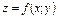имеет непрерывные частные производные, равные нулю в этой точке, тогда, если 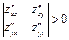, М₀(х₀,у₀) – является экстремумом функции ,

причём, если 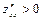, точка М₀ – минимум, если 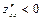, точка М₀ – максимум.

Вектор градиент. Вектор, координаты которого равны частным производным функции 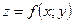, называется вектором градиентом этой функции. .

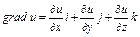Вектор градиент показывает направление максимального возрастания значения функции.

2. Постановка задачи математического программирования (МП).

Операция – управляемое мероприятие, направленное на достижение цели.

Условие задачи математического программирования состоит из:

(1) 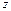= 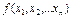- целевой функции, характеризующей зависимость

результата операций от её факторов, переменных ЗМП.

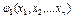
(2) 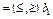системы ограничений, состоящей из m равенств

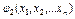
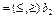или неравенств, показывающих

… связи между факторами операции.,

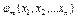
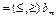
Допустимым решением ЗМП называют любой n-мерный вектор 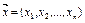, удовлетворяющий системе ограничений (2) и естественному условию неотрицательности переменных

Совокупность всех допустимых решений образуют область в n-мерном пространстве – ОДР.

Решить ЗМП – выбрать из всех допустимых решений то, при котором результат операции будет наилучшим (целевая функция (1) достигнет своего наибольшего или наименьшего значения).

Оптимальным решением ЗМП называется допустимое решение ЗМП, при котором целевая функция 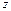= 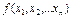достигаетэкстремума.

3. Метод множителей Лагранжа решения ЗМП.

-это общий способ отыскания экстремума функции нескольких переменных, при наличии дополнительных уравнений, связывающих между собой эти переменные (нахождение условного экстремума).

Дано: Целевая функция задачи. =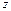

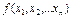
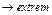
Система уравнений – m ограничений на переменные:

Решение: Составим функцию Лагранжа:

= = + [ - ] +

+ [ - ] + …+ [ - ],

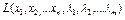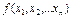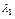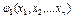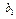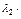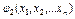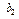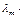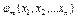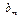где 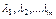- новые неизвестные задачи, множители Лагранжа.

Найдём безусловный экстремум полученной функции. Воспользуемся необходимым условием существования экстремума для функции двух переменных:

Если функция 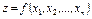достигает экстремума в точке М₀ 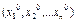, то все её первые частные производные в этой точке равны нулю или не существуют.

Найдём все частные производные этой функции, приравняем их к нулю и составим систему уравнений:

, , …, , , , …,

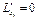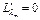
Каждое решение данной системы – критическая точка, принадлежащая ОДР задачи.

Если точек несколько, выбираем из них наибольшее и наименьшее значение.

Если точка единственная, воспользуемся достаточным условием существования экстремума:

Составим матрицу Гессе из вторых частных производных функции Лагранжа.

Если 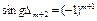и далее знаки главных миноров матрицы чередуются, то критическая точка- точка максимума. Если 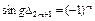и далее знаки чередуются, то критическая точка- точка минимума.

Экономический смысл множителей Лагранжа. Множители Лагранжа 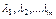указывают, как изменится оптимальное значение целевой функции при изменении соответствующих им параметров задачи 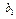, , 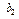…, 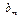на единицу. То есть k-тый множитель Лагранжа определяет ценность k-того ресурса.

4. Графическое решение задач математического программирования.

Рассмотрим ЗМП с двумя неизвестными:

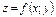
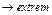- целевая функция 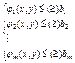- система ограничений

1) Строим ОДР задачи.

Областью решения каждого из неравенств будет часть плоскости, ограниченная линией 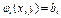. Очевидно, что решением системы неравенств будет пересечение всех их областей решений. ОДР задачи МП – общая часть областей решений всех неравенств системы ограничений.

Если ОДР – пустое множество, задача не имеет решения в силу несовместности системы ограничений.

Если ОДР – непустое множество, задача имеет одно или бесконечное множество решений.

2) Строим линии уровня целевой функции (линии, в которых значение функции постоянно).

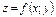=С –уравнения линий уровня.

Если Z – линейная функция, то её линии уровня – семейство прямых, перпендикулярных вектору градиенту этой функции.

Вектором градиентом функции 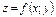называется вектор , координаты которого равны частным производным этой функции.

3) Двигаясь от одной линии уровня к другой в направлении вектора градиента (в задачах на максимум) или в противоположном направлении (в задачах на минимум), находим опорную кривую.

Опорная кривая _ такая линия уровня, которая имеет хотя бы одну общую точку с ОДР, и, при этом, не разделяет её на части.

4) Находим оптимальное решение задачи – общие точки ОДР и опорной кривой.

5. Модель поведения потребителя.

Пусть 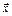= 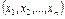- набор из n товаров потребления ( - количество i -го товара, ).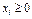

Каждый потребитель определяет для себя ценность любого набора товаров, задавая тем самым функцию потребительского предпочтения, или функцию полезности товара. .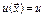

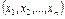Тогда предельная полезность i-го товара - .

Свойства функции полезности:

1)Все её первые частные производные положительны. 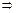возрастание потребления одного продукта при неизменном потреблении других приводит к росту потребительской оценки всего набора.

2) Закон Госсена.

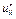<0. 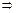предельная полезность любого товара уменьшается с ростом его потребления.

3) Смешанные частные производные второго порядка положительны. 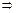предельная полезность любого товара увеличивается с ростом потребления другого.

Линии безразличия функции полезности - линии, соединяющие потребительские наборы, имеющие один и тот же уровень полезности для потребителя. Они не имеют общих точек, не пересекаются и выпуклы вниз.

Поиск по сайту: