 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Естественный и поляризованный свет
По современным физическим представлениям свет представляет собой электромагнитные колебания определенного частотного диапазона. Поэтому математическое описание оптических явлений строится на основе базовых уравнений электромагнетизма - уравнений Максвелла. Одним из важнейших следствий уравнений Максвелла является предсказание существования электромагнитных волн. Свет это электромагнитная волна, в которой происходят синфазные колебания вектора напряженности электрического поля вектора  и вектора напряженности магнитного поля
и вектора напряженности магнитного поля  . Из уравнений Максвелла также следует, что электромагнитная волна поперечна,т.е. колебания векторов
. Из уравнений Максвелла также следует, что электромагнитная волна поперечна,т.е. колебания векторов  и
и  перпендикулярны направлению ее распространения. Таким образом, три вектора
перпендикулярны направлению ее распространения. Таким образом, три вектора  ,
,  и скорость распространения волнового фронта
и скорость распространения волнового фронта  взаимно перпендикулярны и образуют правую тройку векторов.
взаимно перпендикулярны и образуют правую тройку векторов.
Величины, входящие в уравнения Максвелла, связаны дополнительными соотношениями (материальными уравнениями), которые учитывают реакцию среды на внешнее электромагнитное поле.
Как показывает опыт, физиологическое, фотохимическое, фотоэлектрическое и другие действия света вызываются колебаниями электрического вектора. Поэтому его принято называть световым вектором. В дальнейшем мы будем говорить только о векторе  , т.к. направление вектора
, т.к. направление вектора  всегда можно определить, зная направление
всегда можно определить, зная направление  .
.
Свет, испускаемый обычными световыми источниками, есть совокупность световых волн со всевозможными направлениями колебания вектора  в плоскости перпендикулярной к лучу света, быстро и беспорядочно сменяющими друг друга. Такой характер колебаний обусловлен спецификой излучения света. Излучение светящегося тела слагается из электромагнитных волн, испускаемых его атомами. Процесс излучения отдельного атома продолжается около 10-8с. За это время успевает образоваться последователь горбов и впадин (или как, как говорят, цуг волн) протяженностью примерно 3м. Погаснув, атом через некоторое время «вспыхивает» вновь. Одновременно «вспыхивает» много атомов. Возбужденные ими цуги волн, налагаясь друг на друга, образуют испускаемую телом световую волну. Плоскость колебаний для каждого цуга ориентирована случайным образом. Поэтому в результирующей волне колебания различных направлений вектора
в плоскости перпендикулярной к лучу света, быстро и беспорядочно сменяющими друг друга. Такой характер колебаний обусловлен спецификой излучения света. Излучение светящегося тела слагается из электромагнитных волн, испускаемых его атомами. Процесс излучения отдельного атома продолжается около 10-8с. За это время успевает образоваться последователь горбов и впадин (или как, как говорят, цуг волн) протяженностью примерно 3м. Погаснув, атом через некоторое время «вспыхивает» вновь. Одновременно «вспыхивает» много атомов. Возбужденные ими цуги волн, налагаясь друг на друга, образуют испускаемую телом световую волну. Плоскость колебаний для каждого цуга ориентирована случайным образом. Поэтому в результирующей волне колебания различных направлений вектора  представлены с равной вероятностью. Такой свет называется естественным (рис. 1.1(а)).
представлены с равной вероятностью. Такой свет называется естественным (рис. 1.1(а)).
Частично поляризованный свет это свет с преимущественным направлением колебаний вектора  (рис. 1.1(б)).
(рис. 1.1(б)).
Если колебания светового вектора  происходят только в одной проходящей через луч плоскость, то такой свет называется плоско- (или линейно) поляризованным. (рис. 1.1(в)).
происходят только в одной проходящей через луч плоскость, то такой свет называется плоско- (или линейно) поляризованным. (рис. 1.1(в)).




Рис. 1.1
Если вектор  поворачивается вокруг луча, одновременно пульсируя по величине, то в результате конец вектора
поворачивается вокруг луча, одновременно пульсируя по величине, то в результате конец вектора  описывает в пространстве эллипс. Такой свет называется эллиптически-поляризованным(рис. 2). В частном случае, если конец вектора
описывает в пространстве эллипс. Такой свет называется эллиптически-поляризованным(рис. 2). В частном случае, если конец вектора  описывает окружность, свет называется поляризованным по кругу.
описывает окружность, свет называется поляризованным по кругу.
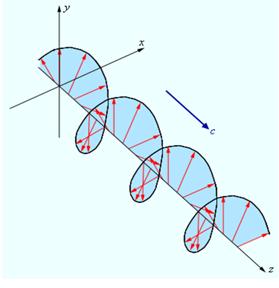
Рис. 1.2. Электрическое поле в эллиптически-поляризованной волне
Для частично поляризованного света вводится понятие степень поляризации. Степенью поляризации называется величина
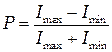
где  и
и 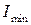 - соответственно, максимальная и минимальная интенсивности частично поляризованного света. Для естественного света
- соответственно, максимальная и минимальная интенсивности частично поляризованного света. Для естественного света  и
и 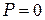 , для плоскополяризованного
, для плоскополяризованного  и
и 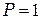 .
.
Естественный свет можно преобразовать в плоскополяризованный, используя так называемые поляризаторы - устройство, содержащее прозрачное вещество,пропускающее колебания только определенного направления. В качестве поляризаторов используются среды, анизотропные в отношении колебаний  .
.
Вещество это система электрических зарядов положительных и отрицательных, в целом скомпенсированных, но под действием электрического поля эти заряды будут смещаться, т.е. вещество будет поляризоваться. В переменном поле направление вектора  меняется через полупериод. В этих условиях атом ведёт себя как электрический осциллятор, имеющий такую же частоту, как и волна. Атом рассеивает электромагнитное излучение благодаря индуцированному колебательному движению зарядов. Когда заряды колеблются относительно друг друга, они излучают электромагнитную волну с той же частотой, с которой происходят колебания самих зарядов. Излучаемая волна имеет сферический фронт, в центре которого находится осциллирующий диполь.
меняется через полупериод. В этих условиях атом ведёт себя как электрический осциллятор, имеющий такую же частоту, как и волна. Атом рассеивает электромагнитное излучение благодаря индуцированному колебательному движению зарядов. Когда заряды колеблются относительно друг друга, они излучают электромагнитную волну с той же частотой, с которой происходят колебания самих зарядов. Излучаемая волна имеет сферический фронт, в центре которого находится осциллирующий диполь.
Взаимодействие электромагнитной волны с конкретным веществом зависят от её состояния поляризации. Например, если мы найдём вещество, в котором заряжённые частицы могут свободно смещаться в направлении оси  и неподвижны в направлении
и неподвижны в направлении  , то в таком веществе компонента
, то в таком веществе компонента  падающей волны будет совершать работу над заряжённой частицей, а компонента
падающей волны будет совершать работу над заряжённой частицей, а компонента  работу не совершит. Энергия электромагнитного излучения, связанная с
работу не совершит. Энергия электромагнитного излучения, связанная с  , уменьшится, (часть ее превратится в кинетическую энергию заряжённых частиц и, в конечном счете, из-за столкновений между частицами — в тепло), в то время как амплитуда
, уменьшится, (часть ее превратится в кинетическую энергию заряжённых частиц и, в конечном счете, из-за столкновений между частицами — в тепло), в то время как амплитуда  от прохождения волны через вещество не изменится. Существуют вещества, которые могут менять разность фаз компонент
от прохождения волны через вещество не изменится. Существуют вещества, которые могут менять разность фаз компонент  и
и  (но не вызывают заметного затухания этих компонент - двойное лучепреломление). В результате таких асимметричных (относительно
(но не вызывают заметного затухания этих компонент - двойное лучепреломление). В результате таких асимметричных (относительно  и
и  -компонент) взаимодействий состояние поляризации электромагнитного излучения изменяется. Этот факт имеет много важных последствий. Зная, как вещество взаимодействует с излучением, мы можем определить состояние поляризация излучения, и, наоборот, наблюдая, как вещество меняет состояние поляризации, мы получаем возможность судить о его свойствах.
-компонент) взаимодействий состояние поляризации электромагнитного излучения изменяется. Этот факт имеет много важных последствий. Зная, как вещество взаимодействует с излучением, мы можем определить состояние поляризация излучения, и, наоборот, наблюдая, как вещество меняет состояние поляризации, мы получаем возможность судить о его свойствах.
Очевидно, что понятие поляризации применимо только к тем волнам, которые имеют, по крайней мере, два независимых направления поляризации. Рассмотрим, например, звуковую волну, распространяющуюся в воздухе вдоль. Если для такой волны известны частота, амплитуда и фаза, то волна определена. Мы знаем, что в звуковой волне смещение происходит вдоль направления распространения волны, т. е. что звуковые волны продольны. В этом случае нет необходимости говорить о продольно-поляризованной волне. Понятие поляризацииприменимо для более сложного случая, когда имеются, по крайней мере, два независимых направления поляризации. У звуковых волн в твёрдом телеили у волн в «пружине» имеются три возможных состояния поляризации — одно продольное и два поперечных. В этом случае можно говорить о волнах с продольной поляризацией или о двух волнах с различной поперечной поляризацией. В общем случае волна может быть суперпозицией всех трех состояний поляризации.
2. ИЗЛУЧЕНИЕ ДИПОЛЯ
Для понимания дальнейшего необходимо сделать небольшое отступление. Зададимся вопросом, что происходит, когда электромагнитная волна попадает в вещество, состоящее из системы электрических зарядов? Очевидно, что происходит смещение положительных зарядов (ядер) в направление вектора  , а электронов в противоположную сторону - вещество поляризуется. Если
, а электронов в противоположную сторону - вещество поляризуется. Если  изменяется по закону
изменяется по закону  , по такому же закону и с той же частотой будет смещаться электроны атомов, т.е. они будут осциллировать. А это значит, что электроны будут двигаться с ускорением.
, по такому же закону и с той же частотой будет смещаться электроны атомов, т.е. они будут осциллировать. А это значит, что электроны будут двигаться с ускорением.
Согласно представлениям классической электродинамики, движущиеся с ускорением электрические заряды, возбуждают электромагнитные волны. Простейшей излучающей системой является осциллирующий электрический диполь, электрический момент  которого изменяется с течением времени, — элементарный вибратор. Возбуждение электромагнитных волн какой-либо системой называют излучением этих волн, а саму систему — излучающей системой. Поле электромагнитной волны называют полем излучения. В нашем случае каждый атом - это излучающий диполь, а среда, в которой распространяется электромагнитная волна – совокупность диполей.
которого изменяется с течением времени, — элементарный вибратор. Возбуждение электромагнитных волн какой-либо системой называют излучением этих волн, а саму систему — излучающей системой. Поле электромагнитной волны называют полем излучения. В нашем случае каждый атом - это излучающий диполь, а среда, в которой распространяется электромагнитная волна – совокупность диполей.
Если излучающая система электронейтральна, а её размеры малы по сравнению с длиной  излучаемых волн, то в точках, отстоящих от системы на расстояниях
излучаемых волн, то в точках, отстоящих от системы на расстояниях  . в так называемой волновой зоне, — поле излучения близко к полю излучения осциллятора, имеющего такой же электрический момент, как и вся излучающая система.
. в так называемой волновой зоне, — поле излучения близко к полю излучения осциллятора, имеющего такой же электрический момент, как и вся излучающая система.
Рассмотрим некоторые закономерности излучения линейного гармонического осциллятора — электрического диполя, размер которого 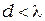 , а момент
, а момент  изменяется во времени по закону
изменяется во времени по закону
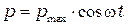 . (2.1)
. (2.1)
где  — амплитудное значение
— амплитудное значение  . Все дальнейшее относится к вакууму, где длина волны
. Все дальнейшее относится к вакууму, где длина волны  ‚ излучения связана с частотой
‚ излучения связана с частотой  соотношением
соотношением  .
.
Напомним, электрическое поле постоянного диполя спадает при удалении от него по закону  . В случае же осциллирующего диполя дело обстоит иначе. В непосредственной близости от диполя картина электромагнитного поля очень сложна. Она сильно упрощается в волновой зоне: быстро спадающее статическое поле практически исчезает и остается только поле излучения от осциллирующих зарядов — расходящаяся сферическая волна с той же частотой, что и у осциллятора. Амплитуда волны (это доказывается в электродинамике) уменьшается с ростом расстояния от диполя как
. В случае же осциллирующего диполя дело обстоит иначе. В непосредственной близости от диполя картина электромагнитного поля очень сложна. Она сильно упрощается в волновой зоне: быстро спадающее статическое поле практически исчезает и остается только поле излучения от осциллирующих зарядов — расходящаяся сферическая волна с той же частотой, что и у осциллятора. Амплитуда волны (это доказывается в электродинамике) уменьшается с ростом расстояния от диполя как
 (2.2)
(2.2)
где  - угол между осью диполя и радиус-вектором
- угол между осью диполя и радиус-вектором  точки, где наблюдается поле (рис. 2.2.). Из этого рисунка видно, что вектор
точки, где наблюдается поле (рис. 2.2.). Из этого рисунка видно, что вектор  в каждой точке волновой зоны направлен по касательной к меридиану, а вектор
в каждой точке волновой зоны направлен по касательной к меридиану, а вектор  — по касательной к параллели, причем так, что в каждый момент векторы
— по касательной к параллели, причем так, что в каждый момент векторы  и
и  составляют правую тройку с вектором Пойнтинга
составляют правую тройку с вектором Пойнтинга  (Рис. 2.1).
(Рис. 2.1).
Факт существования электромагнитного поля, амплитуда которого убывает с расстоянием как  , — поля излучения — весьма важен. Наличие именно такого поля позволяет осуществлять передачи на большие расстояния, видеть звезды.
, — поля излучения — весьма важен. Наличие именно такого поля позволяет осуществлять передачи на большие расстояния, видеть звезды.

Рис. 2.1
Интенсивность электромагнитной волны, т. е. среднее значение плотности потока энергии  , пропорционально произведению
, пропорционально произведению  значит, согласно (2.2):
значит, согласно (2.2):
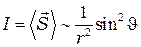 (2.3)
(2.3)
Зависимость  наглядно изображают с помощью диаграммы направленности излучения диполя (рис. 2.1).
наглядно изображают с помощью диаграммы направленности излучения диполя (рис. 2.1).
Здесь длина отрезка  , отсекаемого на луче под углом
, отсекаемого на луче под углом  , дает интенсивность излучения под этим углом. Видно, что максимум излучения происходит в экваториальной плоскости (
, дает интенсивность излучения под этим углом. Видно, что максимум излучения происходит в экваториальной плоскости ( ), а вдоль оси (
), а вдоль оси ( ) диполь не излучает совсем.
) диполь не излучает совсем.

Рис. 2.2
Как показывает теория, мощность излучения  диполя, т. е. энергия, излучаемая в единицу времени по всем направлениям, пропорциональна квадрату второй производной дипольного момента по времени и определяется формулой
диполя, т. е. энергия, излучаемая в единицу времени по всем направлениям, пропорциональна квадрату второй производной дипольного момента по времени и определяется формулой
 (2.4)
(2.4) 
где  (СИ) или
(СИ) или  (СГС). Если зависимость
(СГС). Если зависимость  от
от 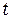 описывается формулой (2.1), то после взятия второй производной по времени получим:
описывается формулой (2.1), то после взятия второй производной по времени получим:
 . (2.5)
. (2.5)
Усреднив (2.5) по времени ( ) получим важный результат:
) получим важный результат:
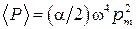 (2.6)
(2.6)
Средняя мощность излучения осциллирующего диполя зависит от квадрата амплитуды дипольного момента  и очень сильно от частоты (как
и очень сильно от частоты (как  ). Отсюда следует, что, например, радиостанции должны использовать высокие частоты, а излучение линий передач переменного тока промышленной частоты оказывается незначительным.
). Отсюда следует, что, например, радиостанции должны использовать высокие частоты, а излучение линий передач переменного тока промышленной частоты оказывается незначительным.
Формула (2.4) справедлива также для излучения заряда  , движущегося ускоренно. В самом деле, дипольный момент можно представить так:
, движущегося ускоренно. В самом деле, дипольный момент можно представить так:  , где
, где  и
и  радиусы векторы зарядов
радиусы векторы зарядов  и
и  . Отсюда
. Отсюда
 ,
,
и если заряд, например, покоится  , а движется только заряд
, а движется только заряд  , то
, то

После подстановки этого выражения в формулу (4) найдем:
 (2.7)
(2.7)
где  — тот же коэффициент, что и в формуле (4).
— тот же коэффициент, что и в формуле (4).
Индексы 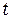 и
и  показывают, что мощность
показывают, что мощность  в момент
в момент 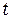 определяется ускорением заряда, которое он имеет в более ранний момент
определяется ускорением заряда, которое он имеет в более ранний момент  (эффект запаздывания). И ещё, формула (2.7), как следует из теории, справедлива лишь для зарядов, движущихся с малыми скоростями (
(эффект запаздывания). И ещё, формула (2.7), как следует из теории, справедлива лишь для зарядов, движущихся с малыми скоростями ( ).
).
В качестве примера можно привести заряженные частицы, движущиеся в циклических ускорителях (бетатроне, циклотроне и др.). Здесь обнаруживается естественный предел для энергии ускоряемой частицы, когда энергия, сообщаемая частице за период, становится равной энергии излучения.
Другой пример — излучение электрона в атоме. По классическим представлениям электрон в атоме совершает колебания, т. е. движется с ускорением и, значит, излучает. Расчёт показывает, что время  , за которое амплитуда колебаний электрона уменьшается в
, за которое амплитуда колебаний электрона уменьшается в  раз, порядка 10-8 с. Это время называют средним временем жизни возбужденного атома, или временем излучения. Точный (квантовый) расчет приводит практически к тому же значению этого времени.
раз, порядка 10-8 с. Это время называют средним временем жизни возбужденного атома, или временем излучения. Точный (квантовый) расчет приводит практически к тому же значению этого времени.
Следует обратить внимание на то, что заряд, колеблющийся с частотой  , излучает монохроматическую электромагнитную волну с той же частотой
, излучает монохроматическую электромагнитную волну с той же частотой  . Если же заряд движется с произвольным ускорением, то его излучение представляет собой спектр различных частот.
. Если же заряд движется с произвольным ускорением, то его излучение представляет собой спектр различных частот.
И последнее, заряд, движущийся в вакууме с постоянной скоростью, не излучает. В этом легко убедиться и непосредственно. Достаточно перейти в систему отсчета, где заряд покоится (а такой заряд не излучает) и затем воспользоваться принципом относительности: если этого явления (излучения) нет в одной системе отсчета, его нет и в других, по отношению к которым заряд движется*
*(Это относится только к движению в вакууме. Если же заряд движется с постоянной скоростью в среде, то в случае, когда его скорость превышает фазовую скорость электромагнитных волн в этой среде, наблюдается излучение Вавилова - Черенкова)
3. ПОЛЯРИЗАЦИЯ ПРИ ОТРАЖЕНИИ И ПРЕЛОМЛЕНИИ СВЕТА НА ГРАНИЦЕ ДВУХ ДИАЛЕКТРИКОВ
Одним из способов получения поляризованного света является его отражение, и преломление на границе раздела двух изотропных диэлектриков.
Если естественный свет падает на границу раздела двух диэлектриков, то отражённый и преломлённый лучи оказываются частично поляризованными.В отражённом луче преобладают колебания перпендикулярные плоскости падения, а в прёломленном колебания, лежащие в плоскости падения.
Если угол падения равен углу Брюстера,который определяется соотношением
 , (3.1)
, (3.1)
то отражённый луч является плоскополяризованным в плоскости перпендикулярной плоскости падения (рис.3.1).

Рис. 3.1
Используя (3.1) нетрудно вычислить величину этого угла:
 . (3.4)
. (3.4)
Например, для границы раздела "воздух-стекло"  .
.
Преломлённый луч в этом случае поляризуется максимально, но не полностью. При этом отражённый и преломлённый лучивзаимно перпендикулярны. Это следует из следующего:
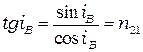 .
.
С другой стороны известно соотношение Снеллиуса:  ,
,
тогда  , что возможно при
, что возможно при 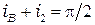 , но
, но  , поэтому
, поэтому
 (3.2)
(3.2)
Брюстеровский угол называют также углом полной поляризации.Действительно, если падающий под этим углом свет деполяризован, то отражённый пучок света линейно поляризован перпендикулярно плоскости падения. Таким образом, эффект Брюстера можно использовать для получения линейно поляризованного света.
Степень поляризации отраженного и преломленного света при различных углах падения можно рассчитать из уравнений Максвелла, если учесть граничные условия для электромагнитного поля на границе раздела двух диэлектриков.
Из сказанного выше следует что, если падающая световая волна поляризована в плоскости падения и выполняется соотношение (3.1)  , то отраженная волна отсутствует (рис.3.2). Этот эффект называют эффектом Брюстера.
, то отраженная волна отсутствует (рис.3.2). Этот эффект называют эффектом Брюстера.

Рис. 3.2. К пояснению эффекта Брюстера
Эффект Брюстера с точки зрения классической теории, объясняется следующим образом. Согласно электромагнитной теории, отражённый луч света представляет собой переизлучение диполей второй среды, при этом выполняется принцип Гюйгенса-Френеля. Из рис. 3.2 видно, что при выполнении условия (3.2)  отражённый и преломлённый лучи оказываются взаимно перпендикулярными. При этом диполи второй среды, колеблются параллельно вектору
отражённый и преломлённый лучи оказываются взаимно перпендикулярными. При этом диполи второй среды, колеблются параллельно вектору  преломлённой волны и, следовательно, перпендикулярно преломлённому лучу.
преломлённой волны и, следовательно, перпендикулярно преломлённому лучу.
С микроскопической точки зрения на границе раздела возникает монослой излучающих диполей, ориентированных перпендикулярно преломлённой волне (что является прямым следствием граничных условий Максвелла). Как было показано выше (см. раздел 2), вдоль своей оси диполь не излучает. Поэтому при перпендикулярности преломлённого и отражённого пучков коэффициент отражения соответствующей поляризации обращается в нуль (рис. 3.2).
В результате отражённый луч отсутствует, и вся энергия света передается преломлённому лучу. Отсюда следует, что эффект Брюстера возможен лишь при поляризации падающего луча в плоскости падения. Если же падающий луч не поляризован или поляризован перпендикулярно плоскости падения, то отражённый луч должен наблюдаться при любом угле падения.
На практике получение линейно поляризованного света за счет отражения под углом Брюстера используется редко из-за низкого коэффициента отражения. Однако возможно построение поляризатора, работающего на пропускание, с использованием стопы Столетова (рис. 3.3).

Рис. 3.3. Стопа Столетова
Стопа Столетова состоит из нескольких плоскопараллельных стеклянных пластинок. При прохождении через неё света под углом Брюстера перпендикулярная компонента практически полностью рассеивается на границах раздела, а прошедший луч оказывается, поляризован в плоскости падения. Такие поляризаторы используются в мощных лазерных системах, в которых поляризаторы других типов могут быть разрушены лазерным излучением.
4. АНАЛИЗ ПОЛЯРИЗОВАННОГО СВЕТА. ЗАКОН МАЛЮСА
Существует много разных способов получения поляризованного света. Устройства, которые позволяют получать поляризованное излучение, называют поляризаторами. Анализ поляризованного света осуществляется с помощью поляризационных приборов. Если поляризационный прибор используется для получения поляризованного света, то он называется поляризатором. При использовании прибора для анализа поляризованного света его называют анализатором.
Простейшим примером поляризатора является поляроид. Он состоит из тонкого слоя маленьких кристаллов герапатита (соль йода и хинина), выстроенных своими осями параллельно друг другу. Эти кристаллы поглощают свет, когда колебания происходят вдоль оси, в направлении котором выстроены кристаллы, и почти не поглощают света, когда колебания совершаются в перпендикулярном направлении. Направление, перпендикулярное направлению, вдоль которого выстроены молекулы, называют осью свободного пропускания поляроида. Если поле  направлено вдоль этой оси, то свет проходит практически без поглощения.
направлено вдоль этой оси, то свет проходит практически без поглощения.
Направим на идеальный поляроид естественный свет и выберем одно колебание со случайным световым вектором  , у которого плоскость колебания составляет угол
, у которого плоскость колебания составляет угол  с осью свободного пропускания. Разложим вектор
с осью свободного пропускания. Разложим вектор  на две компоненты, параллельную
на две компоненты, параллельную  и перпендикулярную оси
и перпендикулярную оси  свободного пропускания
свободного пропускания  , как показано на рис. 4.1.
, как показано на рис. 4.1.
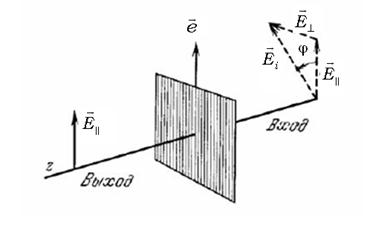
Рис.4.1. Прохождение света через поляроид. Ось пропускания направлена по  .
.  составляющая
составляющая  , параллельная
, параллельная  , проходит. Вторая составляющая
, проходит. Вторая составляющая  , перпендикулярная
, перпендикулярная  , полностью поглощается
, полностью поглощается
Перпендикулярная компонента  полностью поглотится, в случае идеального поляризатора. Через поляроид пройдет только компонента
полностью поглотится, в случае идеального поляризатора. Через поляроид пройдет только компонента  , т.е. часть пропорциональная
, т.е. часть пропорциональная  .
.
Амплитуда элементарной световой волны, прошедшего через поляроид  , меньше амплитуды падающей волны
, меньше амплитуды падающей волны  , и равна
, и равна  . Интенсивность света связана с амплитудой
. Интенсивность света связана с амплитудой 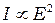 , тогда интенсивность прошедшего через первый поляроид света
, тогда интенсивность прошедшего через первый поляроид света 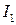 определиться следующим соотношением:
определиться следующим соотношением:
 . (4.1)
. (4.1)
Это соотношение называют законом Малюса. Здесь  - угол между осью свободного пропускания поляроида и направлением колебания случайного вектора
- угол между осью свободного пропускания поляроида и направлением колебания случайного вектора  . Суммарная амплитуда всего потока света определится суммой
. Суммарная амплитуда всего потока света определится суммой  . В естественном свете все значения
. В естественном свете все значения  равновероятны, поэтому доля света, прошедшего через поляризатор, будет равна среднему значению
равновероятны, поэтому доля света, прошедшего через поляризатор, будет равна среднему значению  , а интенсивность плоскополяризованного света, прошедшего через первый поляризатор П 1:
, а интенсивность плоскополяризованного света, прошедшего через первый поляризатор П 1:
 (4.2)
(4.2)
Поставим на пути плоскополяризованного света второй идеальный поляризатор П 2, (анализатор) под углом  к первому (Рис. 4.2) После прохождения первого поляризатора мы получаем плоскополяризованный свет, колебания электрического вектора которого лежат в его плоскости пропускания. Интенсивность
к первому (Рис. 4.2) После прохождения первого поляризатора мы получаем плоскополяризованный свет, колебания электрического вектора которого лежат в его плоскости пропускания. Интенсивность  света, прошедшего через второй поляризатор (анализатор), меняется в зависимости от угла
света, прошедшего через второй поляризатор (анализатор), меняется в зависимости от угла  по закону Малюса:
по закону Малюса:
 (4.3)
(4.3)
где  - угол между осями пропускания первого и второго поляризаторов.
- угол между осями пропускания первого и второго поляризаторов.

|
Следовательно, интенсивность света, прошедшего через два поляризатора:
 (4.4)
(4.4)
где  угол между осями пропускания первого и второго поляризаторов.
угол между осями пропускания первого и второго поляризаторов.
Отсюда следует, что интенсивность света прошедшего два поляризатора максимальна, когда оси пропускания поляризаторов параллельны ( ), и равна
), и равна  . Когда поляризаторы «скрещены» (
. Когда поляризаторы «скрещены» ( ) интенсивность свете минимальна и равна нулю
) интенсивность свете минимальна и равна нулю  .
.
5. ОПТИЧЕСКАЯ АНИЗОТРОПИЯ И ОСНОВНЫЕ ЭФФЕКТЫ КРИСТАЛЛОПТИКИ
5.1. Двойное лучепреломление поляризация при двойном лучепреломлении
Некоторые кристаллы обладают необычными оптическими свойствами. Например, кристалл исландского шпата (кальцит - СаСо3) преломляет свет по-разному в зависимости от того, с какой стороны падает свет на кристалл. В этом кристалле есть одно направление, вдоль которого при нормальномпадении луч света проходит прямолинейно (рис. 5.1а).
Прямая, проведенная через любую точку кристалла в этом направлении, называется оптической осью.
По количеству оптических осей, имеющихся у данного кристалла, различают одноосные и двухосные кристаллы. В дальнейшем речь будет идти только об одноосных кристаллах. Плоскость, содержащая оптическую ось и падающий луч, называют главным сечением или главной плоскостью кристалла.
В других направлениях луч, проходя через кристалл, раздваиваетсяи образуется два пучка примерно одинаковой интенсивности (рис. 5.1б). Луч проходящий прямо называют обыкновенным лучом (о), а другой — необыкновенным (е).
Это явление называется двойным лучепреломлением, а зависимость оптических свойств, например, показателя преломления, от направления в кристалле называют оптической анизотропией. В естественных условиях оптически анизотропными является большинство кристаллов.

Рис. 5.1. Прохождение света вдоль оси исландского шпата (а). Двойное лучепреломление света, падающего нормально к естественной грани кристалла исландского шпата (б)
При повороте кристалла относительно оси падающего пучка пятно, соответствующее обыкновенному лучу, на экране остается неподвижным, а второе, соответствующее необыкновенному, поворачивается вокруг первого синхронно с поворотом кристалла (рис. 5.2б).

Рис. 5.2. Картины, наблюдаемые на экране в опытах с кристаллом исландского шпата (а, б). Поляризация лучей (в)
Анализ поляризации лучей с помощью поляроида показывает, что оба луча, вышедших из кристалла, линейно поляризованы, причем направления поляризации в них взаимно ортогональны (Рис. 5.2в).
У одноосных кристаллов для обыкновенного луча выполняется обычный закон преломления:
 , (5.3)
, (5.3)
этот луч лежит в одной плоскости с падающим лучом и нормалью к преломляющей поверхности. Скорость этого луча во всех направлениях одинакова.
Для необыкновенного луча отношение  при изменении угла падения и, соответственно, скорость распространения этого луча различна в разных направлениях.
при изменении угла падения и, соответственно, скорость распространения этого луча различна в разных направлениях.
Причиной оптической анизотропииявляется анизотропия структуры среды. Анизотропия среды может быть обусловлена как анизотропией составляющих ее частиц, так и характером их расположения. В частности, изотропная среда может быть построена из анизотропных частиц, а анизотропная – из частиц изотропных. Оптическая анизотропиясреды характеризуется различной по разным направлениям способностью реагировать на действие падающего света. Реакция эта состоит в смещении электрических зарядов под действием поля световой волны.
Из теории Максвелла следует, что фазовая скорость распространения света в среде
 , (5.1)
, (5.1)
где  – показатель преломления вещества;
– показатель преломления вещества;  – скорость света в вакууме;
– скорость света в вакууме;  – диэлектрическая проницаемость вещества;
– диэлектрическая проницаемость вещества;  – магнитная проницаемость вещества;
– магнитная проницаемость вещества;  и
и  электрическая и магнитная постоянные.
электрическая и магнитная постоянные.
Для большинства оптически прозрачных веществ магнитная проницаемость  » 1, поэтому, показатели преломления и скорости света в среде определяются величиной диэлектрической проницаемости среды
» 1, поэтому, показатели преломления и скорости света в среде определяются величиной диэлектрической проницаемости среды
 . (5.2)
. (5.2)
Свойства изотропных сред одинаковы по всем направлениям и в таких средах  имеет одно определенное значение. В таких средах, скорость распространения света с любой поляризацией для любого направления одинакова и поэтому волновой фронт световой волны сферический.
имеет одно определенное значение. В таких средах, скорость распространения света с любой поляризацией для любого направления одинакова и поэтому волновой фронт световой волны сферический.
Свойства анизотропных сред зависят от направления. В частности, от направления в среде зависит значение её диэлектрической проницаемости  , а значит и скорость распространения света. В этом случае фронт распространения световой волны внутри анизотропного кристалла представляет собой эллипсоид вращения. В местах пересечения с оптической осью кристалла и сфера, построенная для обыкновенных лучей, и эллипсоид для необыкновенных – соприкасаются.
, а значит и скорость распространения света. В этом случае фронт распространения световой волны внутри анизотропного кристалла представляет собой эллипсоид вращения. В местах пересечения с оптической осью кристалла и сфера, построенная для обыкновенных лучей, и эллипсоид для необыкновенных – соприкасаются.
Одноосные кристаллы характеризуют показателем преломления обыкновенного луча, равным  , и показателем преломления необыкновенного луча, перпендикулярного к оптической оси, равным
, и показателем преломления необыкновенного луча, перпендикулярного к оптической оси, равным  . Последнюю величину называют просто показателем преломления необыкновенного луча.
. Последнюю величину называют просто показателем преломления необыкновенного луча.

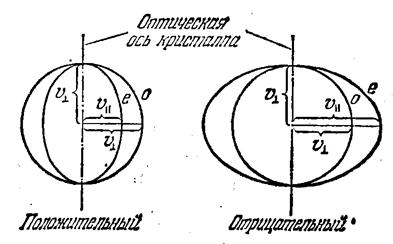
Рис. 5.3
В зависимости от того, какая из скоростей,  или
или  , больше, различают положительные и отрицательные одноосные кристаллы (рис. 5.3). У положительных кристаллов
, больше, различают положительные и отрицательные одноосные кристаллы (рис. 5.3). У положительных кристаллов  (это означает, что
(это означает, что  ). У отрицательных кристаллов наоборот
). У отрицательных кристаллов наоборот 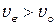 (
( ).
).
Ход обыкновенного и необыкновенного лучей в кристалле можно определить с помощью принципа Гюйгенса. На рис. 5.4 построены волновые поверхности обыкновенного и необыкновенного лучей с центром в точке 2, лежащей на поверхности кристалла.

Рис. 5.4
Построение выполнено на момент времени, когда волновой фронт падающей волны достигает точки 1. Огибающие всех вторичных волн для обыкновенного и необыкновенного лучей, очевидно, представляют собой плоскости. Преломленный луч о или е, выходящий из точки 2, проходит через точку касания огибающей с соответствующей волновой поверхностью.
Плоскость колебаний вектора  обыкновенного луча перпендикулярна главному сечению кристалла (на рис. 5.4 эти направления показаны точками). В необыкновенном луче колебания светового вектора происходят в плоскости главного сечения (на рис. 5.4) они показаны двухсторонними стрелками). При выходе из кристалла оба луча отличаются друг от друга только направлением поляризации.
обыкновенного луча перпендикулярна главному сечению кристалла (на рис. 5.4 эти направления показаны точками). В необыкновенном луче колебания светового вектора происходят в плоскости главного сечения (на рис. 5.4) они показаны двухсторонними стрелками). При выходе из кристалла оба луча отличаются друг от друга только направлением поляризации.
На рис. 5.5 изображены три случая нормального падения света на поверхность кристалла, отличающиеся различным направлением оптической оси. В случае (а) лучи о и е распространяются вдоль оптической оси и поэтому идут не разделяясь.
|
|


|
|

Из рис. 5.5б видно, что даже при нормальном падении света на преломляющую поверхность необыкновенный луч может отклониться от нормали к этой поверхности. На рис. 5.5в оптическая ось кристалла параллельна преломляющей поверхности. В этом случае при нормальном падении света обыкновенный и необыкновенный лучи идут по одному и тому же направлению, но распространяются с разной скоростью, вследствие чего между ними возникает все возрастающая разность фаз. Характер поляризации обыкновенного и необыкновенного лучей таков же, как для лучей, изображенных на рис. 5.4.
5.2. Прохождение плоскополяризованного света через кристаллическую пластинку
Пусть плоскополяризованный свет падает перпендикулярно на кристаллическую пластинку толщиной  . Пластинка вырезана из кристалла так, что оптическая ось кристалла параллельна ее поверхности (случай (в) на рис.5.5). Пусть угол между плоскостью колебаний вектора
. Пластинка вырезана из кристалла так, что оптическая ось кристалла параллельна ее поверхности (случай (в) на рис.5.5). Пусть угол между плоскостью колебаний вектора  падающего света и оптической осью
падающего света и оптической осью  равен a (рис. 5.6).
равен a (рис. 5.6).
Колебания вектора  падающего плоскополяризованного света в некоторой точке пространства можно представить как результат сложения взаимно перпендикулярных колебаний, направленных вдоль и поперёк направления оптической оси кристалла. При этом вид поляризации волны до ее падения на кристалл будет определяться разностью фаз
падающего плоскополяризованного света в некоторой точке пространства можно представить как результат сложения взаимно перпендикулярных колебаний, направленных вдоль и поперёк направления оптической оси кристалла. При этом вид поляризации волны до ее падения на кристалл будет определяться разностью фаз  этих взаимно перпендикулярных колебаний. При разности фаз
этих взаимно перпендикулярных колебаний. При разности фаз  и
и  радиан падающая на кристалл волна будет плоскополяризованной. При разности фаз
радиан падающая на кристалл волна будет плоскополяризованной. При разности фаз  и
и  радиан, поляризованной по эллипсу.
радиан, поляризованной по эллипсу.

Рис. 5.6. Вид на пластинку сверху.
Внутри кристалла падающий луч разделится на «обыкновенный» и «необыкновенный» лучи, амплитуды светового вектора в которых будут равны:
 (5.4)
(5.4)
Скорости распространения лучей в пластинке различны, поэтому внутри пластинки между ними накопится дополнительная разность фаз колебаний векторов  и
и  .
.
Эту разность фаз можно найти следующим образом. Поскольку волны входят в кристалл перпендикулярно его оптической оси, то их геометрические пути в кристалле будут одинаковы и равны толщине кристалла (рис.5.5в). Вместе с тем оптические длины путей для «обыкновенного» и «необыкновенного» лучей из-за различия в показателях преломления будут различны. Возникающая в кристалле оптическая разность хода волн равна
 . (5.5)
. (5.5)
Поиск по сайту: