Иваново

МЕТОДЫ ОПТИМИЗАЦИИ

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

И ЗАДАНИЯ К ПРАКТИЧЕСКИМ ЗАНЯТИЯМ

И ЛАБОРАТОРНЫМ РАБОТАМ

Иваново

Министерство высшего и среднего специального образования РСФСР

Ивановский ордена Трудового Красного Знамени

химико-технологический институт

МЕТОДЫ ОПТИМИЗАЦИИ

Методические указания и задания к практическим

занятиям и лабораторным работам

Составители: С.И.Смуров

Т.В.Сокольская

В.А.Бобкова

Иваново 1990

Составители: С.И.Смуров, Т.В.Сокольская, В.А.Бобкова

УДК 519.85(07)

Методы оптимизации: Методические указания и задания к практическим занятиям и лабораторным работам / Иванов. Хим. - технол. ин-т;

Сост. С.И.Смуров, Т.В.Сокольская, В.А.Бобкова. Иваново, 1990. 72 с.

В методических указаниях изложены основные методы одномерной и многомерной оптимизации. Приведены блок-схемы соответствующих алгоритмов, числовые примеры, задания для самостоятельной работы.

Данные методические указания могут быть использованы студентами всех форм обучения при изучении темы “Оптимизация”.

Табл.9. Библигр.: 8 назв.

Редактор Л.Л.Торгашева

Техн. Редактор О.Ю.Дикушина

Корректор И.Г.Клюкина

Подписано в печать 23.01.90. Формат бумаги 60x84 I/I6. Печ.л.4,5.

Уч.-изд.л.З. Усл.кр.-отт.З. Тираж 800 экз. Заказ 552/р. Бесплатно.

Ивановский химико-технологический институт.

Типография УУЗ Минэнерго СССР, 153025, г. Иваново, ул. Ермака, 41

ВВЕДЕНИЕ

Оптимизация - это целенаправленная деятельность, заключающаяся в получении наилучших результатов при соответствующих условиях.

Количественная оценка оптимизируемого качества называется критериемоптимальности или целевой функцией. Её можно записать в виде:

(1)

где 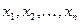- некоторые параметры объекта оптимизации.

Существуют два типа задач оптимизации - безусловные и условные.

Безусловная задача оптимизации состоит в отыскании максимума или минимума* действительной функции (1) от n действительных переменных и определении соответствующих значений аргументов на некотором множестве n -мерного пространства.

Условные задачи оптимизации, или задачи с ограничениями, - это такие, при формулировке которых на значения аргументов налагаются ограничения в виде равенств:

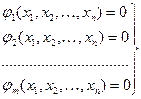(2)

или неравенств:

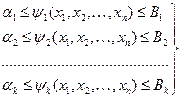(3)

Решение задач оптимизации, в которых критерий оптимальности является линейной функцией независимых переменных с линейными ограничениями на них, составляет предмет линейного программирования.

При n = 1 целевая функция R является функцией одной переменной. В этом случае говорят об одномерной оптимизации.

* Отметим, что задача отыскания максимума функции R эквивалентно задаче отыскания минимума функции - R. Это позволяет без труда переносить результаты, полученные для задачи минимизации, на задачи максимизации, и наоборот. В дальнейшем, как правило, будет рассматриваться задача минимизации.

1. МЕТОДЫ ОДНОМЕРНОЙ ОПТИМИЗАЦИИ

1.1. Метод сканирования [1, 2]

Метод сканирования в качестве критерия движения к минимуму использует сравнительную оценку величины целевой функции, вычисленной в соответствующих точках.

Интервал поиска (a, b) разбивается на несколько равных участков, каждый из которых равен шагу поиска h (рис.1).

Далее последовательно определяются значения функции f(x) во всех точках разбиения аргумента и в точках a и b и запоминается наименьшее значение. Таким образом, минимум может быть найден с точностью до h.

Достоинства метода: простота, возможность нахождения глобального минимума.

Недостаток метода: большой объём вычислений, которые необходимо выполнить при его реализации.

Метод сканирования эффективен при использовании ЭВМ.

Блок схема алгоритма поиска минимума целевой функции R=f(x) методом сканирования.

1.2. Метод локализации [1,2]

Алгоритм метода:

1. Интервал поиска минимума (a,b) разбивается на четыре равные части (подынтервалы) точками 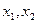и (рис.3).

2. Вычисляются значения целевой функции R=f(x) во всех точках разбиения и в точках x=a, x=b.

3. Полученные значения f(x) сравниваются между собой, и из них выбирается наименьшее.

4. Локализуют минимум, причем новый интервал поиска равен двум старым подынтервалам с наименьшим значением f(x) на их общей границе (на рис.3 это соответствует интервалу (a, )).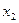

5. Делят интервал, в котором локализован минимум, опять на четыре равных подынтервала (на рис.3 точками ) и снова вычисляют значения критерия оптимальности в точках деления, сравнивают их между собой, находят наименьшее, локализуют минимум в меньшем интервале (на рис.3 в интервале ()) и так далее до тех пор, пока минимум не будет локализован в интервале, размер которого соответствует заданной точности поиска.

Замечание. Интервал поиска разбивается именно на четыре подынтервала с целью уменьшения объема вычислений: при этом каждый последующий подынтервал делиться пополам, и вычислять значение функции нужно только в двух новых точках, так как её значения на концах нового интервала и его середине известны из предыдущих расчетов.

Длина интервала неопределенности после S вычислений значений целевой функции определяется выражением:

, (4)

абсолютная ошибка в нахождении минимума составляет:

(5)

Пример.

Найти минимум целевой функции в области 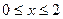, локализовав его на отрезке длиной не более 0,3.

Решение

Первый шаг.

Разбиваем интервал поиска 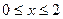на четыре равные части и вычисляем значения функции f(x) на концах интервала и в точках разбиения:

a = 0 f(a) = 0

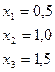
b = 2 f(b) = 90,0

Минимальное значение целевой функции есть =f(1,0)=-11,7.

Интервал поиска уменьшаем, ограничивая точками 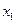=0,5, =1,5, т.е. локализуем экстремум в области .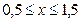

Второй шаг.

Новый интервал поиска 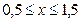разбиваем на четыре равные части и вычисляем значения целевой функции в точках разбиения и на концах интервала.

Значение функции:

f(0,5) = -9,16; f(1,0) = -11,67; f(1,5) = 11,32

вычислены ранее на предыдущем этапе, поэтому вычисляем лишь:

f(0,75) = -12,12 и f(1,25) = -5,02.

Выбираем минимальное значение:

f(0,75) = -12,12,

и интервал поиска вновь уменьшаем, т.е. локализуем экстремум в области .

Третий шаг.

Новый интервал поиска разбиваем на четыре равные части.

Значения f(0,5) = -9,16; f(0,75) =- 12,12; f(1) = -11,67

вычислены на втором этапе, поэтому вычисляем только

f(0,625) = -10,93; f(0,875) = -12,48.

Из всех значений функции выбираем минимальное f(0,875) = -12,48 и локализуем экстремум в области .

Расчет окончен, т.к. экстремум локализован в области v X = 0,25 < 0,3 с точностью v = 0,125.

Ответ: 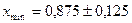; f(0,875) = -12,48.

1.3. Метод золотого сечения [1-7]

При построении процесса оптимизации стараются сократить объем вычислений и время поиска. Этого достигают обычно путем сокращения количества вычислений значений целевой функции f(x). Одним из наиболее эффективных методов, в которых при ограниченном количестве вычислений f(x) достигается наилучшая точность, является метод золотого сечения.

Если известно, что функция f(x) унимодальна* на отрезке [a,b], то положение точки минимума можно уточнить, вычислив f(x) в двух внутренних точках отрезка. При этом возможны две ситуации:

. Минимум реализуется на отрезке [a, ].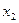

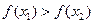. Минимум реализуется на отрезке [ 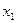,b].

В методе золотого сечения каждая из точек 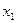и 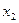делит исходный интервал на две части так, что отношение целого к большей части равно отношению большей части к меньшей, т.е. равно так называемому “золотому сечению”. Это соответствует следующему простому геометрическому представлению:

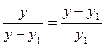Здесь или . (6)

Обозначив 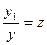, получаем ,

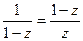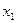откуда . Итак, длины отрезков [a, ] и [ 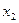,b] одинаковы и составляют 0,382 от длины (a,b). По значениям f(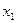) и f(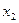) определяется новый интервал (a, 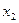) или (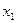,b), в котором локализован минимум. Найденный интервал снова делится двумя точками в том же отношении, причем одна из новых точек деления совпадает с уже использованной на предыдущем шаге.

Взаимное расположение точек первых трех вычислений можно показать следующим образом:

1)

Первый шаг

Второй шаг

2)

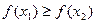
Первый шаг

Второй шаг

Таким образом, длина интервала неопределенности на каждом шаге снижается с коэффициентом 0,618. На первом шаге необходимы два вычисления функции, на каждом последующем - одно.

Длина интервала неопределенности после S вычислений значений f(x) составляет

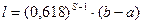. (7)

Алгоритм метода золотого сечения для минимизации функции f(x) складывается из следующих этапов:

1. Вычисляется значение функции f(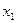), где .

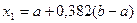2. Вычисляется значение функции f(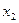), где .

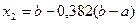3. Определяется новый интервал (a, 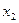) или (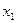,b), в котором локализован минимум.

4. Внутри полученного интервала находится новая точка (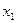 в случае 1) или ( 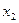в случае 2), отстоящая от его конца на расстоянии, составляющем 0,382 от его длины. В этой точке рассчитывается значение f(x), затем вычисления повторяются, начиная с пункта 3, до тех пор, пока величина интервала неопределенности

станет меньше или равна 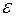, где 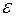- заданное сколь угодно малое положительное число.

Блок-схема алгоритма поиска минимума функции f(x) методом золотого сечения.

Пример.

Используя метод золотого сечения, минимизировать функцию 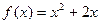на интервале (-3,5). Длина конечного интервала неопределенности не должна превосходить 0,2.

Решение.

Первый шаг. a = - 3, b = 5, b - a = 8.

. Новый отрезок.

Второй шаг. a = - 3, b = 1,944, b - a = 4,944.

. Новый отрезок.

Дальнейшие вычисления оформим в виде таблицы. Значения функции, вычисленные на каждом шаге, помечены звездочкой.

После восьми шагов, содержащих девять вычислений функции, интервал неопределенности равен, его длина. В качестве точки минимума может быть взята середина этого интервала -1,024; при этом. Заметим, что точкой точного минимума является -1,0;.

1.4. Метод поиска с использованием чисел Фибоначчи [1,3-6]

Последовательность чисел Фибоначчи определяется соотношением:

, (8)

и имеет вид

0 1 2 3 4 5 6 7 8 9 10 11 12

1 1 2 3 5 8 13 21 34 55 89 144 233 и т.д.

Подобно методу золотого сечения процедура поиска с использованием чисел Фибоначчи требует два вычисления функции на первом шаге, а на каждом последующем - только по одному. Однако, в отличии от

метода золотого сечения, в этой процедуре общее число S вычислений функции должно быть выбрано заранее. Кроме того, сокращение интервала неопределенности не остается постоянным, а меняется от шага к шагу:

на K -ом шаге длина интервала неопределенности сжимается с коэффициентом.

Первые два вычисления проводятся в точках и, расположенных симметрично относительно середины отрезка. Если, то новым отрезком локализации минимума является, в случае. Каждая следующая точка выбирается симметрично относительно середины полученного отрезка к лежащей внутри этого отрезка точке уже проведенного вычисления (или). При этом любая внутренняя точка делит отрезок локализации в отношении двух последовательных чисел Фибоначчи.

Взаимное расположение точек первых трех вычислений в случае показано на рис.7.

Первый шаг

Второй шаг

После (S - 1)-го шага точка проведенного вычисления оказывается в середине отрезка локализации. Точка последнего, S -го, шага выбирается на расстоянии от середины этого отрезка, где - заранее фиксированное малое положительное число (константа различимости).

После S вычислений функции длина отрезка локализации составляет (с точностью до)

. (9)

Сравнение (9) и (7) показывает, что при одном и том же S метод Фибоначчи дает меньший интервал неопределенности, чем метод золотого сечения, т.е. является более эффективным. Однако для достаточно больших S значение стремиться к, так что эти методы становятся почти идентичными.

В том случае, когда при использовании метода Фибоначчи задан конечный интервал неопределенности, число S можно определить из условия:

.

Алгоритм минимизации функции с использованием чисел Фибоначчи.

1. По заданной точности рассчитывается вспомогательное число:

2. Для полученного значения N находится такое число Фибоначчи, для которого выполняется неравенство

.

3. По формуле (9) определяется длина конечного интервала неопределенности.

4. Вычисляются значения

5. В зависимости от соотношения и выбирается новый интервал локализации минимума.

6. Внутри полученного интервала находится новая точка (или), симметричная к уже имеющейся точке и отстоящая от конца интервала на величину, где K - номер шага. В этой точке рассчитывается

значение. Затем вычисления повторяются, начиная с пункта 5, до тех пор, пока K не станет равно S - 1. Тогда переходят к пункту 7.

7. Полагают, находят. Если, то минимум реализуется на интервале, в противном случае - на интервале.

Блок-схема описанного алгоритма приведена на рис.8.

Пример.

С помощью метода Фибоначчи найти минимум функции на интервале. Длина конечного интервала неопределенности не должна превосходить 0,2.

Решение.

Примем.

Найдём необходимое число вычислений функции:

,.

Итак, S = 9.

.

Первый шаг. a = -3; b = 5.

. Новый отрезок.

Второй шаг. a = -3; b = 1,9445.

. Новый отрезок.

Дальнейшие расчеты приведены в таблице 2. Значения, вычисленные на каждом шаге, помечены звездочкой.

Поскольку для K = 9, конечный интервал неопределенности равен, длина его составляет 0,1455. В качестве приближенного значения точки минимума выберем середину этого отрезка -1,0358;. Напомним, что при использовании метода золотого сечения при S = 9 длина интервала неопределенности была равна 0,176.

1.5. Задания.

Найти положение точки экстремума и экстремальное значение функции на интервале. Длина конечного интервала неопределенности не должна превышать 0,01.

2. МНОГОМЕРНЫЙ ПОИСК. НЕЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ.

МЕТОДЫ БЕЗУСЛОВНОЙ МИНИМИЗАЦИИ [1,2,6 - 8]

2.1. Постановка задачи

Напомним, что общая задача нелинейной программирования без ограничений сводится к следующей: минимизировать функцию на всем евклидовом пространстве.

Методы решения задач безусловной минимизации можно разделить на две группы: безградиентные и градиентные.

Эти методы носят итерационный характер, т.е. процесс поиска минимума целевой функции с заданной точностью заключается в построении некоторой конечной последовательности точек. При этом соседние точки последовательности связаны соотношением:

(11)

или

(12)

Здесь индекс “i” определяет номер составляющей вектора, индекс “k” - номер шага поиска, вектор характеризует направление поиска, скаляра - величину шага.

Таким образом, выполнение одной (k-ой) итерации (или шага) заключается в выборе направления и определении точки на данном направлении, где

.

2.2. Выбор длины шага

Пусть известна точка. Необходимо найти координаты точки

для этого сделаем шаг в направлении и определим его величину.

Основная задача при выборе - обеспечить выполнение неравенства.

При выборе шага обычно используют способ удвоения или методы

одномерной минимизации, описанные выше.

Способ удвоения состоит в следующем:

Выбирают. Если при этом, то либо

переходят к следующей ()-й итерации, либо выбирают.

Если значение функции меньше предыдущего, то процесс удвоения можно

продолжать до тех пор, пока убывание не прекратиться.

Если при значение функции, т.е., то выбирают. Уменьшение значения

функции позволяет вести дальнейший поиск. Увеличение требует нового

изменения и т.д.

Выбор длины шага методами одномерной минимизации основан

на поиске минимума функции.

Часто для этой цели используется метод квадратичной интерполяции,

алгоритм, которого можно представить следующими этапами.

1) В заданной точке принимают. Выбирают длину шага такой,

чтобы. В качестве третьей точки берут значение.

2) Вычисляют три значения.

3) Находят коэффициенты параболы, проходящей через три выбранные

узла интерполяции, из уравнений

4) Функция будет иметь минимум в точке

Вычисляют положение экстремума.

5) Проверяют выполнение условия. Если оно не выполняется, то

, и вычисления повторяются с пункта 1.

При выполнении этого условия продолжают поиск с шагом.

Кроме метода квадратичной интерполяции для выбора шага

можно использовать метод золотого сечения, кубической интерполяции,

сканирования и т.д.

Величину шага можно выбирать также из условия минимума

функции, т.е. из условия. При этом

где - некоторая константа или определитель

для точки.

Условие связано с величиной косинуса угла

между направлением вектора градиента и направлением

движения из этой же точки:

2.3. Выбор направления поиска

Методы безусловной минимизации различаются выбором направления

поиска, но всегда направление выбирают таким, чтобы значение

целевой функции уменьшалось, т.е. чтобы выполнялось условие.

2.3.1. Безградиентные методы. Покоординатный спуск.

Наиболее простым способом определения направления спуска

является выбор в качестве одного из координатных векторов.

Это позволяет поочередно изменять все независимые переменные так,

чтобы на каждой из них достигалось наименьшее значение целевой функции.

Очередность варьирования независимых переменных при этом устанавливается

произвольно и не меняется в процессе поиска. В результате

многомерный поиск заменяется последовательностью одномерных поисков

с любой стратегией минимизации функции одной переменной

(см. методы, описанные выше).

Данный метод эффективен в случае единственного минимума функции.

Для уменьшения числа вычислений величину шага меняют при каждом

переходе от поиска минимума по одной переменной к поиску минимума

по другой переменной.

Алгоритм метода может быть представлен следующими этапами.

1. Задают исходную точку поиска.

2. Определяют направление поиска; если варьируется переменная

3. Делают первый шаг в направлении.

Значение выбирают способом удвоения или минимизацией

функции по. Если аналитическое выражение целевой функции достаточно простое,

для выбора можно использовать условие.

4. После определения положения минимума по координате делают

шаг в направлении

Значение находят, минимизируя функцию, и так далее.

5. Поиск заканчивают при выполнении условия

Пример

Пусть целевая функция имеет вид

Требуется найти её минимум с точностью.

Решение.

1. Примем в качестве исходной точки. Значение целевой функции в этой точки

2. Направление поиска выберем параллельно координатной оси

3. Изменим переменную.

Значение найдём из условия

Итак, нашли точку, в которой значение целевой функции

4. Изменим переменную

Значение найдём из условия

Тогда

Нашли точку

5. От точки вновь изменим направление поиска и сведём дальнейшие вычисления в таблицу 4.

После четвертой итерации выполняется условие окончания поиска:

Ответ: минимум целевой функции находится в точке

Отметим, что точный минимум целевой функции находится в точке

Рассмотрим на другом примере покоординатный спуск с использованием для выбора величин шага способа удвоения. Соответствующая блок-схема представлена на рис.9.

Пусть требуется минимизировать функцию, начиная с точки.

1. Изменим переменную

Найдем, применяя способ удвоения.

Блок-схема метода покоординатного спуска с удвоением шага.

Выберем произвольное значение

Тогда

Удвоим шаг:

При этом

Ещё раз удвоим шаг:

Тогда

Уменьшение целевой функции позволяет ещё удвоить шаг:

При этом

Функция не уменьшилась. Следовательно, наилучшее значение. Точка, найденная с таким значением, имеет координаты.

2. Ещё раз изменим переменную

Примем

Тогда

Функция не уменьшилась. Уменьшим шаг вдвое:

При этом

3. Сделаем шаг по переменной

Примем

Тогда

4. Ещё раз изменим переменную

где

Тогда

5. Ещё раз изменим переменную с таким же значением

6. Следующий шаг по с тем же параметром приводит к возрастанию функции:

Следовательно, функция является точкой минимума целевой функции.

2.3.2. Градиентные методы.

Градиентные методы связаны с поиском по направлению градиента или антиградиента оптимизируемой функции.

Градиент функции обозначается и определяется как вектор-столбец из первых частных производных этой функции:

В каждой точке градиент ортогонален линии уровня

, проходящей через эту точку, и направлен в сторону наискорейшего возрастания функции.

Вектор-антиградиент также ортогонален линии уровня, проходящей через данную точку, но направлен в сторону наискорейшего убывания функции. Таким образом, вектор, указывающий направление поиска при минимизации функции, есть.

Процедура вычисления производных целевой функции весьма трудоемка. На практике их часто приходится вычислять приближенно, пользуясь разностными соотношениями. Например, для функции двух переменных разностные формулы имеют вид

где - некоторые малые приращения аргументов.

Величины выбираются так, чтобы ошибка аппроксимации производной не превышала разумного уровня.

В общем случае при отыскании минимума целевой функции схема перехода из точки в точку определяется не просто антиградиентом, а произведением антиградиента на симметричную, положительно определенную матрицу. Алгоритм метода при этом имеет вид

Числа выбираются согласно 2.2. В частности, можно для определения -ом шаге использовать косинус угла (между последовательными векторами переходов в процесс спуска от точки к точке

Тогда

В качестве и можно принять, например, углы в, соответственно.

Модификации градиентных методов

В зависимости от выбора матриц градиентные методы делятся на метод наискорейшего спуска, метод изменения масштабов, метод сопряженных направлений, метод Ньютона, метод Давидона-Флетчера-Пауэлла и другие.

Рассмотрим две модификации - наискорейший спуск и метод сопряженных направлений.

2.3.2.1. Метод наискорейшего спуска.

При, т.е. когда является единичный матрицей, алгоритм записывается как

Здесь индекс “i” характеризует номер составляющей вектора, индекс определяет номер итерации поиска, определяется из условия минимума функции или по формуле.

Алгоритм такого метода, называемого методом наискорейшего спуска, можно представить следующими этапами.

1. Задают исходную точку

Оценивают направление поиска путем вычисления частных производных в точке

2. Делают переход от точки к точке по формуле

3. Вновь определяют направление спуска, вычисляя частные производные в полученной точке

4. Делают переход к точке

И так далее

При этом параметр можно рассматривать как константу, а можно оценить или способом удвоения или методом одномерной минимизации функции

5. Поиск заканчивают, если

или

где - малая положительная величина.

Пример

Требуется минимизировать функцию, начиная с точки, с точностью

Решение.

1. Определим направление поиска, вычисляя производные в заданной точке:

2. Выберем из условия

Пусть, тогда точка имеет координаты

При этом

Следовательно, необходимо уменьшить.

Примем, тогда

При этом

3. Сделаем переход в точку, корректируя по формулам

Поскольку, в соответствии с примем. Тогда

4. Вновь определим направление поиска, вычисляя производные в точке, скорректируем, и все дальнейшие итерации сведём в таблицу 5.

На шестнадцатой итерации выполняется условие окончания поиска

Ответ: минимум целевой функции находится в точке

Графическая иллюстрация данного примера приведена на рис.11.

Строим линии уровня целевой функции. Задавая некоторые постоянные значения функции, получаем каноническое уравнение эллипса:

при; при

и так далее.

2.3.2.2. Метод сопряженных напряжений

В методе сопряженных напряжений строится последовательность направлений поиска, являющихся линейными комбинациями градиента и предыдущих направлений.

Алгоритм метода выражается следующими расчетными формулами:

Здесь - весовые коэффициенты, одним из способов, определения которых служит формула

Ниже приводятся этапы этого алгоритма.

1. В исходной точке вычисляют градиент как начальное направление поиска, т.е.

2. По формуле (25) находят точку с координатами, минимизируя функцию по с помощью методов одномерного поиска.

3. Вычисляют в точке значение функции и значение градиента

4. Определяют новое направление поиска из соотношения

и так далее.

5. Поиск заканчивают при выполнении условия

Алгоритм метода может предусматривать обновление через итераций, тогда точка становится исходной, и поиск вновь начинается с направления антиградиента функции. Блок-схема метода приведена на рис.12.

Пример.

Требуется минимизировать функцию, начиная сточки. Принять = 0,5.

1. Вычисляем частные производные целевой функции в исходной точке, тем самым, задавая начальное направление поиска:

2. Длину шага определяем по формуле (13)

Находим координаты точки:

3. Вычисляем значения:

4. Определяем новое направление поиска

5. Оцениваем длину шага

Точка имеет координаты

И так далее. На рис. 13 изображена траектория поиска, результаты расчетов сведены в таблицу 6.

На пятой итерации выполняется условие окончания поиска:

Ответ: минимум целевой функции находится в точке

2.4. Задания

Найти минимум (максимум) функции с точностью

3. МНОГОМЕРНЫЙ ПОИСК. НЕЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ. МЕТОДЫ УСЛОВНОЙ МИНИМИЗАЦИИ [1,2,6-8]

3.1. Метод сканирования

Как и в случае одной переменной метод сканирования для случая многих переменных заключается в последовательном просмотре значений целевой функции в ряде точек, принадлежащих области изменения независимых переменных, и нахождении среди них такой. в которой целевая функция имеет минимальное значение.

Точность метода определяется частотой расположения выбранных точек на данной области изменения переменных.

Алгоритм метода сканирования для функции многих переменных заключается в следующем.

1. Исследуется функция цели вдоль одного выбранного направления (вдоль одной из координатных осей) с шагом. В каждой точке вычисляется и запоминается значение целевой функции.

2. После того, как весь диапазон изменения выбранной переменной исследован и для него найдено минимальное значение целевой функции, изменяется значение другой переменной на величину шага, и опять исследуется диапазон вдоль оси первой переменной, и т.д.

Графическая иллюстрация поиска минимума для случая двух переменных дана на рис.14.

Для произвольного числа переменных шаг по каждой следующей переменной производится после того, как завершен цикл по предыдущей.

Если имеются ограничения на независимые переменные, то точки, которые не удовлетворяют уравнениям (или неравенствам) ограничений, исключаются из рассмотрения.

Если точность поиска по каждой из переменных равна, то количество целевой функции, необходимых для поиска минимума, составит

где n - число переменных.

Недостаток метода: велико число вычислений, которое резко возрастает (в показательной степени) в зависимости от размерности решаемой задачи.

Преимущества метода: простота алгоритма, возможность определения глобального минимума.

Методы сканирования, в основном, используются для грубого анализа областей расположения минимумов.

3.2. Метод штрафных функций

Основная идея метода штрафных функций состоит в преобразовании задачи минимизации функции с соответствующими ограничениями, наложенными на аргументы в задачу поиска минимума функции без ограничений.

Преимущество, которое получаем в результате такого перехода к новой функции, достигается за счет применения более простых алгоритмов.

Методы штрафных функций можно разделить на два класса: параметрические и непараметрические. Параметрические методы характеризуются наличием одного или нескольких параметров, входящих в структуру штрафной функции в качестве весовых коэффициентов.

Например, требуется найти минимум функции

при ограничениях

Введём функцию

Здесь выступает в роли штрафа. Штраф можно выбрать в виде

или в виде

где - некоторый положительный параметр.

Примеры выбора вида штрафной функции:

Пусть дана функция при ограничениях. Выберем штраф как

В результате минимизируем функцию

Другой пример. Требуется минимизировать функцию при ограничении

Прибавим к целевой функции значение, тогда получим функции без ограничений

Таким образом, метод штрафных функций определяются как выбором вида штрафа, так и выбором параметра.

Рассмотрим на конкретном примере один из параметрических методов, а именно метод внутренней точки.

Пусть требуется минимизировать функцию при ограничениях

Исходная точка поиска.

1. Строим функцию без ограничений, используя штраф

2. Пусть. Найдем минимум функции любым методом безусловной оптимизации, например, градиентным:

И так далее.

3. Уменьшаем

Минимизируем тем же градиентным методом, теперь за исходную точку принимаем

4. Вновь уменьшаем

Чем ближе к минимуму при, тем меньше градиент функции

Поиск заканчивается, если, где - малая положительная величина.

Графическая иллюстрация примера показана на рис.15.

Линии уровня функции есть концентрические окружности с центром в точке с координатами

3.3. ЗАДАНИЯ. Минимизировать при заданных ограничениях функцию с точностью.

4. МНОГОМЕРНЫЙ ПОИСК. ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ [1,2]

Линейные модели - это такие модели, где математические зависимости линейны относительно всех переменных величин, включенных в моделей (т.е. содержат эти переменные в первой степени).

Методом решения таких задач, как уже говорилось, является линейное программирование. Слово “программирование” отражает здесь конечную цель исследования - определение оптимального плана или оптимальной программы, по которой из множества возможных вариантов исследуемого процесса выбирают по какому-либо признаку наилучший, оптимальный, вариант.

Примером такой задачи является задача оптимального распределения сырья между различными производствами при максимальной стоимости продукции.

Пусть из двух видов сырья изготавливается продукция двух видов.

Обозначим:

- число единиц продукции вида 1 и 2, соответственно;

- цена единицы продукции вида 1 и 2, соответственно;

Тогда общая стоимость всей продукции будет

В результате производства желательно, чтобы общая стоимость продукции была максимальной. R - целевая функция в данной задаче.

Обозначим:

- количество сырья 1-го и 2-го видов, имеющееся в наличии, - число единиц -го вида сырья, необходимое для производства единицы -го вида продукции.

Учитывая, что расход данного ресурса не может превышать общего его количества, запишем ограничительные условия по ресурсам:

Относительно переменных можно еще сказать, что они неотрицательны

Среди множества решений системы неравенств (32) и (33) требуется найти такое решение, для которого функция R достигает наибольшего значения.

В таком же виде формулируются так называемые транспортные задачи (задачи оптимальной организации доставки товаров, сырья или продукции из различных складов к нескольким пунктам назначения при минимуме затрат на перевозку) и ряд других.

4.1. Математическая формулировка задачи линейного программирования.

Найти совокупность значений переменных, удовлетворяющих системе ограничений

и условиям неотрицательности

где

для которых линейная целевая функция R

достигает экстремума (максимума или минимума).

Выражения (34),(35),(36) образуют линейную математическую модель общей задачи линейного программирования.

Любая совокупность значений удовлетворяет еще условиям (35), то она называется допустимым решением или допустимый план задачи.

Совокупность возможных допустимых решений (планов) задачи называют областью допустимых решений задачи.

Допустимое решение, для которого целевая функция (36) достигает максимума (или минимума), называется оптимальным решением (оптимальным планом) задачи.

Ограничительные условия (34) могут состоять только из уравнений (), только из неравенств или из уравнений и неравенств. В первых двух случаях они называются однородными, а в третьем - смешанными условиями.

4.2. Графический метод решения задач линейного программирования.

Задача.

Найти и, удовлетворяющие системе неравенств

условиям неотрицательности

для которых функция

достигает максимума.

Решение. Построим в системе прямоугольник координат область допустимых решений задачи. Для этого, заменяя каждое из неравенств (37) равенством, строим соответствующую ему граничную прямую

Эта прямая делит плоскость на две полуплоскости, для координат любой точки одной полуплоскости выполняется неравенство, а для координат любой точки граничной прямой удовлетворяют уравнению

Для определения, по какую сторону от граничной прямой располагается полуплоскость, соответствующая заданному неравенству, достаточно “испытать” одну какую-нибудь точку (проще всего точку O(0,0)). Если при подстановке её координат в левую часть неравенства оно удовлетворяется, то полуплоскость обращена в сторону к испытуемой точке, если же неравенство не удовлетворяется, то соответствующая полуплоскость обращена в противоположную сторону. Направление полуплоскости показывается на чертеже (рис.17) штриховкой.

Неравенствам и также соответствует полуплоскости, расположенные справа от оси ординат и над осью абсцисс.

На рисунке строим граничные прямые и полуплоскости, соответствующие всем неравенствам.

Общая часть (пересечение) всех этих полуплоскостей будет представлять собой область допустимых решений данной задачи.

При построении области допустимых решений в зависимости от конкретного вида степени ограничений (неравенств) на переменные может встретиться один из четырех случаев (рис.18).

Область допустимых решений пустая, что соответствует несовместности системы неравенств; решения нет.

Область допустимых решений изображается одной точкой, что соответствует единственному решению системы.

Область допустимых решений ограниченная, изображается в виде выпуклого многоугольника. Допустимых решений множество.

Область допустимых решений неограниченная, в виде выпуклой многоугольной области. Допустимых решений множество.

Графическое изображение целевой функции при фиксированном значении определяет прямую, а при изменении - семейство параллельных прямых с параметров.

Вектор, перпендикулярный ко всем этим прямым, показывает направление возрастания.

Для всех точек, лежащих на одной из этих прямых, функция принимает одно определенное значение, поэтому указанные прямые называется линиями уровня для функции (рис.19).

Задача отыскания оптимального решения системы неравенств (37), для которого целевая функции (39) достигает максимума, геометрически сводится к определению в области допустимых решений точки, через которую пройдет линия уровня, соответствующая наибольшему значению параметра.

Если область допустимых решений есть выпуклый многоугольник, то экстремум функции достигается, по крайней мере, в одной из вершин этого многоугольника.

Если экстремальное значение достигается в двух вершинах, то же экстремальное значение достигается в любой точке на отрезке, соединяющем эти две вершины. В этом случае говорят, что задача имеет альтернативный оптимум.

В случае неограниченной области экстремум функции либо не существует, либо достигается в одной из вершин области, либо имеет альтернативный оптимум.

Пример.

Найти и, удовлетворяющие системе неравенств

условиям неотрицательности

для которых функция

достигает максимума

Решение.

1. Заменим каждое из неравенств неравенством и построим граничные прямые (рис.20)

Определим полуплоскости, соответствующие данным неравенствам (40) путем “испытания ” точки (0,0). Покажем направления полуплоскостей штриховкой (рис.21). С учетом неотрицательности и получим область допустимых решений данной задачи в виде выпуклого многоугольника.

3. В области допустимых решений находим оптимальное решение, строя вектор, который показывает направление возрастания (рис.21).

Оптимальное решение соответствует точке, координаты которой можно определить либо графически; либо путем совместного решения двух уравнений, соответствующих граничным прямым и, т.е.

Ответ:

4.3. Симплексный метод решения задач линейного программирования.

Симплексный метод реализует идею последовательного улучшения решения. Это универсальный метод, который может быть применен при решении любой задачи линейного программирования.

Задача.

Найти решение системы уравнений

удовлетворяющее условиям неотрицательности

и максимизирующее линейную функцию

Полагая, что ранг матрицы коэффициентов меньше числа неизвестных, выразим неизвестных системы (41) через остальные

В системе (44) число линейно независимых уравнений равно.

Неизвестные можно придавать любые неотрицательные значения, то свободные члены должны быть неотрицательными. В противном случае (т.е. если для) при получим, что недопустимо по условию задачи.

Положим все свободные неизвестные равные нулю:

Получим

Полученное решение системы является допустимым, т.к. удовлетворяет условиям (41) и (42), и называется базисным решением. При этом вектор называется базисным вектором.

Подставим в оптимизируемую линейную функцию (43) найденные базисные неизвестные, выраженные через свободные неизвестные. Для первого базисного решения все свободные неизвестные, поэтому получим.

Далее переходим к другому базисному решению. При этом значение оптимизируемой линейной функции должно увеличиваться (если ищем максимум) или уменьшаться (если ищем минимум).

Переход осуществляется следующим образом: одна из базисных переменных заменяется другой, которая ранее была свободной, и т.д. Этот процесс повторяется до тех пор, пока не достигнет экстремального значения.

Рассмотрим принцип нахождения решения задачи линейного программирования на примерах.

Пример 1.

Найти решение системы уравнений

Удовлетворяющее условиям неотрицательности

и минимизирующее целевую функцию

Выразим базисные переменные через свободные и:

Приняв свободные переменные и равными нулю, получим первое базисное решение, т.е. выполним первую итерацию симплексных преобразований:

При этом R = 3.

Выполним вторую итерацию, которая приведет к уменьшению.

Анализ уравнения (47), которое определяет, показывает, что целевая функция может быть уменьшена за счет уменьшения и увеличения. Однако уменьшить нельзя, т.к. на первой итерации, а условие неотрицательности не позволяет сделать

Значит, путь уменьшения состоит в увеличении.

Увеличение должно идти до тех пор, пока одна из переменных, которая зависит от, не станет равной нулю и, следовательно, дальнейшее увеличение приведет к отрицательному значению, что недопустимо.

Из системы (48) следует, что не может превышать значения 2, т.к. при становится меньше нуля (первое уравнение системы (48)), что недопустимо по условию задачи.

Принимаем, при этом. Подставим эти значения в систему уравнений (48), получим новое базисное решение:

При этом

Выразим новые базисные переменные через свободные:

Подставив полученное выражение для в выражение для целевой функции (47), получим

Поскольку требуется получить минимум функции, а уже на второй итерации и равны нулю, то, учитывая, что и не могут быть отрицательными, а любое увеличение и не приводит к уменьшению, делаем вывод: задача решена, и искомое решение есть результат второй итерации (50).

Пример.

Найти значения, которые удовлетворяют системе уравнений

условиям неотрицательности

и обеспечивает наименьшее значение целевой функции

Примем переменные в качестве базисных и выразив их через свободные переменные из уравнения (52). Получим

Первое базисное решение примет вид

При этом

Из уравнения (54) видно, что целевая функция может быть уменьшена путем увеличения и. Увеличим сначала. Из (55) следует, что можно увеличить до значения, поскольку при большем его значении переменная станет отрицательной.

Полагая из (55) получаем второе базисное решение

При этом

Примем ненулевые переменные в качестве базисных, а нулевые переменные в качестве свободных. Из системы (52) найдем

Выражение для целевой функции (54) запишем через свободные параметры, заменив с помощью (58). Получим

Отсюда следует, что значение целевой функции можно изменить за счет увеличения, поскольку коэффициент при этой переменной в (59) отрицательный.

Максимальное значение определяется соотношениями (58) и составляет. Из (58) при получаем третье базисное решение.

При этом

Для проведения следующего шага симплексных преобразований ненулевые переменные в (60), т.е. нужно принять в качестве базисных, а нулевые переменные - в качестве свободных. В этом случае целевую функцию можно записать в виде

Поскольку коэффициенты при положительные, то при увеличении этих параметров целевая функция возрастает. Следовательно, решение (60) является оптимальным.

4.4. Задания

Найти минимум (максимум) целевой функции при заданных ограничениях

ЛИТЕРАТУРА

1. Бояринов А.И., Кафаров В.В. Методы оптимизации в химической технологии. -М.:Химия, 1975. -576 с.

2. Турчак Л.И. Основы численных методов: Учеб.пособие.-М.:Наука. Гл.ред.физ.-мат.лит., 1987. -320с.

3. Базара М., Шетти К. Нелинейное программирование. Теория и алгоритмы: Пер.с англ.-М.:Мир, 1982. -583с.

4. Сухарев А.Г., Тимохов Л.В., Федоров В.В. Курс методов оптимизации.-М.:Наука, Гл.ред.физ.-мат.лит., 1986. -328с.

5. Гилл Ф., Мюррей У., Райт М. Практическая оптимизация:Пер.с англ.-М.:Мир, 1985. -509с.

6. Банди Б. Методы оптимизации. Вводный курс:Пер с англ.-М.:Радио и связь,, 1988. -128с.

7. Химмельблау Д. Прикладное нелинейное программирование.-М.:Мир, 1975. -535с.

8. Карманов В.Г. Математическое программирование.-М.: Наука, 1980. -256с.

СОДЕРЖАНИЕ

Введение

1. Методы одномерной оптимизации

1.1 Метод сканирования

1.2 Метод локализации

1.3 Метод золотого сечения

1.4 Метод поиска с использованием чисел Фибоначчи

1.5 Задания

2. Многомерный поиск. Нелинейное программирование. Методы безусловной минимизации.

2.1. Постановка задачи

2.2. Выбор длины шага

2.3. Выбор направления поиска

2.3.1. Безградиентные методы. Покоординатный спуск

2.3.2. Градиентные методы

2.3.2.1. Метод наискорейшего спуска

2.3.2.2. Метод сопряженных направлений

2.4. Задания

3. Многомерный поиск. Нелинейное программирование. Методы условной минимизации.

3.1. Метод сканирования

3.2. Метод штрафных функций

3.3. Задания

4. Многомерный поиск. Линейное программирование

4.1. Математическая формулировка задачи

4.2. Графический метод решения задач

4.3. Симплексный метод решения задач

4.4. Задания

Литература

Поиск по сайту: