Эллиптическая поляризация света

Поляризованное излучение имеет в общем случае эллиптическую поляризацию. При этом ортогональные компоненты светового вектора для выбранной системы координат (ось Z параллельна направлению распространения света) описываются выражениями вида:

, (1)

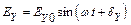. (2)

Сложение ортогональных колебаний вида (1) и (2) на плоскости XY дает проекционную картину эллипса. При этом форма эллипса определяется параметрами

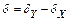– разность фаз, (3)

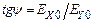– отношение амплитуд. (4)

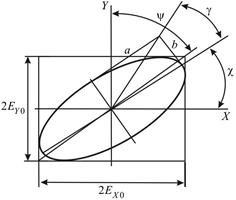
Рис. 2. Схематическое изображение эллиптически поляризованного света.

При значении 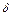, равном нулю или 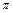, эллипс вырождается в прямую линию и получается линейно поляризованный свет. При и равенстве амплитуд складываемых волн эллипс превращается в окружность - получается свет, поляризованный по кругу.

В зависимости от направления вращения вектора различают правую и левую эллиптическую поляризацию. Если по отношению к направлению луча вектор вращается по правилу правого винта, поляризация называется правой, в противном случае - левой.

Для описания формы эллипса часто используют другую пару параметров, имеющих более наглядную геометрическую интерпретацию (рис. 2):

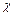– азимут ориентации большой полуоси эллипса в выбранной системе координат;

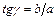– эллиптичность - отношение полуосей эллипса.

Связь между параметрами 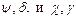задается формулами:

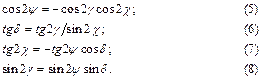
Представление эллипса поляризации двумя парами параметров и соотношение между ними имеют важное практическое значение. Непосредственно измеряемыми параметрами в большинстве измерительных схем являются величины 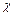и 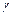, для физической интерпретации результатов измерений часто более удобны параметры 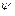и 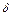(например, при построении математической модели объекта с использованием законов и формул Френеля для обработки результатов измерений).

Поиск по сайту: