 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Создание отчета
Отчет можно создать тремя различными способами.
При помощи автоотчета на основе таблицы или запроса. Автоотчет служит для создания отчета, в котором выводятся все поля и записи базовой таблицы или запроса.
Инструкции
1. В окне базы данных нажмите кнопку Отчеты  на панели Объекты.
на панели Объекты.
2. Нажмите кнопку Создать на панели инструментов окна базы данных.
3. В диалоговом окне Новый отчет выберите одного из следующих мастеров.
Автоотчет: в столбец — каждое поле располагается на отдельной строке; подпись находится слева от поля.
Автоотчет: ленточный — поля каждой записи находятся на отдельной строке; подписи печатаются сверху, один раз для каждой страницы.
4. Выберите таблицу или запрос, содержащие данные, на которых должен быть основан отчет.
5. Нажмите кнопку OK.
Microsoft Access применяет последний автоформат, использовавшийся для создания отчета. Если до этого отчет с помощью мастера не создавался и не использовалась команда Автоформат в меню Формат, то будет применен стандартный автоформат.
При помощи мастера на основе одной или нескольких таблиц или запросов. Мастер задает подробные вопросы об источниках записей, полях, макете, требуемых форматах и создает отчет на основании полученных ответов.
Инструкции
В окне базы данных нажмите кнопку Отчеты  на панели Объекты.
на панели Объекты.
1. Нажмите кнопку Создать на панели инструментов окна базы данных.
2. В диалоговом окне Новый отчет выберите нужного мастера. Описание действий, выполняемых мастером, выводится в левой половине диалогового окна.
3. Выберите таблицу или запрос, содержащие данные, на которых должен быть основан отчет.
Примечание. Если на шаге 3 в списке выбран Мастер отчетов, то этот шаг не обязателен — можно указать источник записей для отчета в мастере.
4. Нажмите кнопку OK.
5. Следуйте инструкциям мастера.
Созданный отчет можно изменить в режиме конструктора.
Вручную в режиме конструктора. Сначала создается базовый отчет, который затем изменяется в соответствии с требованиями в режиме конструктора.
Инструкции
1. В окне базы данных нажмите кнопку Отчеты  на панели Объекты.
на панели Объекты.
2. Нажмите кнопку Создать на панели инструментов окна базы данных.
3. В диалоговом окне Новый отчет выберите пункт Конструктор.
4. Выберите таблицу или запрос, содержащие данные, на которых должен быть основан отчет. (Если нужно создать свободный отчет, не выбирайте ничего из этого списка.)
2.12. Каковы общая формулировка задачи линейного программирования и средства ее решения в процессоре Excel?
Линейное программирование – это математическая дисциплина, изучающая методы нахождения экстремальных значений функций нескольких переменных, удовлетворяющих конечному числу линейных неравенств или уравнений.
Функция, для которой определяется экстремальное значение, называется целевой. Системы неравенств и уравнений, которым должны удовлетворять переменные целевой функции, называются системами ограничений.
Оптимальным называется допустимое решение, в котором целевая функция достигает экстремального значения.
В общем виде в задаче линейного программирования требуется найти:

при условии

Здесь:
xj – переменные.
aij, bi, cj – константы
Система ограничений задачи линейного программирования включает m уравнений. При m = n задача имеет одно решение. При m < n возможно множество решений, среди которых можно найти оптимальное.
Для общей постановки задачи линейного программирования ограничения неравенств должны быть преобразованы в уравнения. Это может быть достигнуто добавлением к левой части каждого ограничения дополнительных неотрицательных величин. В частности неравенство
am1x1 + am2x2 + … + amnxn ≤ bm
может быть преобразовано в уравнение
am1x1 + am2x2 + … + amnxn + xn+m = bm
Неравенство
am1x1 + am2x2 + …+ amnxn ≥ bm
Может быть преобразовано в уравнение
am1x1 + am2x2 + …+ amnxn – xn+m = bm
Экономический смысл введенной переменной xn+m – дополнительный ресурс.
При любом характере ограничений задачи линейного программирования, в конечном счете, приводятся к общей форме
am1x1 + am2x2 + … + amnxn – bm = 0
Модель задачи линейного программирования должна содержать только линейные уравнения и неравенства, т.е. все переменные должны иметь первую степень.
Оценка экономической эффективности производства
P Основная задача оптимизации – это поиск и идентификация наиболее приемлемого варианта решения.
Практическая деятельность менеджера финансового учреждения, производственной или непроизводственной сферы связана с непрерывным поиском наиболее эффективных методов использования финансовых, производственных, временных и человеческих ресурсов, обеспечивающих принятие управляющих и инженерных решений. Чаще всего такой вариант экстремален: это максимум прибыли, минимум себестоимости и отходов производства и т.п.
Задача на минимум себестоимости

при условиях

Задача на минимум капиталовложений

при условиях

Задача на максимум прибыли

при условиях

В приведенных формулах приняты следующие обозначения:
B – требуемый объем производства,
K – лимит капитальных вложений,
xi – объем производства продукции по варианту i (i= 1, 2,…, m),
ci – себестоимость производства продукции по варианту i,
ki – удельные капитальные вложения при производстве по варианту i,
pi – прибыль полученная при реализации варианта i.
Постановка оптимизационной задачи
Правильная постановка задачи оптимизации – это основа ее успешного решения. Математическая модель должна:
ó отражать связь между переменными,
ó определять содержание целевой функции,
ó определять ограничения.
Постановка оптимизационной задачи может включать такие этапы:
ó содержательная, то есть неформализованная постановка задачи,
ó формализация,
ó определение типа и принципа решения задачи,
ó установка границ оптимизируемой системы,
ó определение количественных критериев для анализа различных вариантов.
Для решения задач такого типа в Excel имеется средство Поиск решения.

Элементы диалогового окна «Поиск решения»
Установить целевую ячейку
Служит для указания целевой ячейки, значение которой необходимо максимизировать, минимизировать или установить равным заданному числу. Эта ячейка должна содержать формулу.
Равно
Служит для выбора варианта оптимизации значения целевой ячейки (максимизация, минимизация или подбор заданного числа). Чтобы установить число, введите его в поле.
Изменяя ячейки
Служит для указания ячеек, значения которых изменяются в процессе поиска решения до тех пор, пока не будут выполнены наложенные ограничения и условие оптимизации значения ячейки, указанной в поле Установить целевую ячейку.
Предположить
Используется для автоматического поиска ячеек, влияющих на формулу, ссылка на которую дана в поле Установить целевую ячейку. Результат поиска отображается в поле Изменяя ячейки.
Ограничения
Служит для отображения списка граничных условий поставленной задачи.
Добавить
Служит для отображения диалогового окна Добавить ограничение.
Изменить
Служит для отображения диалоговое окна Изменить ограничение.
Удалить
Служит для снятия указанного ограничения.
Выполнить
Служит для запуска поиска решения поставленной задачи.
Закрыть
Служит для выхода из окна диалога без запуска поиска решения поставленной задачи. При этом сохраняются установки сделанные в окнах диалога, появлявшихся после нажатий на кнопки Параметры, Добавить, Изменить или Удалить.
Параметры
Служит для отображения диалогового окна Параметры поиска решения, в котором можно загрузить или сохранить оптимизируемую модель и указать предусмотренные варианты поиска решения.
Восстановить
Служит для очистки полей окна диалога и восстановления значений параметров поиска решения, используемых по умолчанию.
2.13. Какие задачи решают корреляционный и регрессионный анализ?
Корреляционный и регрессионный анализ позволяет исследовать взаимосвязи двух и более числовых рядов и моделировать числовые ряды, элементы которых получены в определенные моменты времени (временные ряды).
Пусть имеется несколько числовых рядов:
Y = {y1, y2, …, yn}
X1 = {x1,1, x1,2, …, x1,n}
X2 = {x2,1, x2,2, …, x2,n}
...
Xm = {xm,1, xm,2, …, xm,n}
Качественный анализ показал, что эти ряды, возможно, связаны причинно-следственной нефункциональной связью, и ряд Y зависит от остальных. Величины X1,X2,…,Xm называются факторами..
Корреляционный анализ позволяет оценить силу связи числовых рядов друг с другом, а регрессионный анализ позволяет построить уравнение регрессии Y = F(X1,X2,…,Xm), являющееся статистической моделью некоторого процесса. Наиболее распространена линейная модель, описывающаяся уравнением:
Y = amXm + am-1Xm-1 + … +a1X1 + a0
При проведении регрессионного анализа следует отобрать значимые факторы, имеющие существенное значение, и отбросить незначимые.
Табличный процессор Excel имеет соответствующий инструментарий для выполнения корреляционного и регрессионного анализа. При подготовке данных числовые ряды следует располагать в вертикальных рядах, т.к. ряд встроенных функций и приложений ориентирован на такое расположение данных.
Оценка силы связи двух числовых рядов для линейной модели выполняется по линейному коэффициенту парной корреляции. Он вычисляется с помощью встроенной функции КОРРЕЛ, аргументами которой являются координаты областей, содержащих значения числового ряда. Существуют критические значения коэффициента корреляции, зависящие от доверительной вероятности и числа элементов числовых рядов, которые позволяют сделать вывод о значимости или незначимости коэффициента корреляции и, следовательно, о существовании или отсутствии линейной связи между рядами.
Для построения уравнения регрессии можно применить встроенные функции ЛИНЕЙН и ОТРЕЗОК. Первая из них позволяет определить коэффициенты a1, a2, …, am, а вторая – коэффициент a0 для случая парной регрессии. Аргументами функций являются:
· известные_значения_y – это множество значений элементов ряда y;
· известные_значения_x – это множество значений элементов рядов x;
· константа – признак обязательного равенства нулю коэффициента a0 (применяется только для функции ЛИНЕЙН);
· статистика – признак необходимости построения статистического описания линейного уравнения регрессии вплоть до проверки нулевой гипотезы для уравнения в целом и его коэффициентов (только для функции ЛИНЕЙН).
Кроме указанных встроенных функций можно рекомендовать встроенный пакет анализа данных, поставляемый как отдельная надстройка процессора Excel. Пакет анализа имеет ряд приложений, позволяющих выполнить дисперсионный и корреляционный анализ, а также построить уравнение регрессии и выполнить его исследование на значимость самого уравнения и его коэффициентов.
Временной ряд имеет три компоненты: тенденцию (тренд), периодическую составляющую и случайную составляющую. Для моделирования временных рядов применяются аддитивная и мультипликативная модели. Первая модель предусматривает вычисление значения элемента временного ряда как сумму компонент, а вторая – как произведение.
Перед началом анализа временного ряда необходимо выполнить сглаживание временного ряда с целью устранения случайных воздействий. Процессор Excel предоставляет для этой цели в пакете анализа данных две процедуры: сглаживание методом скользящей средней и экспоненциальное сглаживание. Далее во временном ряду выделяются значения тренда и периодической составляющей. После выделения значений тренда выполняется моделирование тренда аналитической функцией времени. Для этой цели в пакете анализа имеется приложение "Тенденция".
Корреляционный анализ дает возможность установить, ассоциированы ли наборы данных по величине, то есть, большие значения из одного набора данных связаны с большими значениями другого набора (положительная корреляция), или, наоборот, малые значения одного набора связаны с большими значениями другого (отрицательная корреляция), или данные двух диапазонов никак не связаны (нулевая корреляция). Коэффициент корреляции, как ковариационный анализ, характеризует область, в которой два измерения "изменяются вместе". В отличие от ковариационного анализа коэффициент масштабируется таким образом, что его значение не зависит от единиц, в которых выражены переменные двух измерений (например, если вес и высота являются двумя измерениями, значение коэффициента корреляции не изменится после перевода веса из фунтов в килограммы). Любое значение коэффициента корреляции должно находится в диапазоне от -1 до +1 включительно.
Линейный регрессионный анализ заключается в подборе графика для набора наблюдений с помощью метода наименьших квадратов. Регрессия используется для анализа воздействия на отдельную зависимую переменную значений одной или более независимых переменных. Например, на спортивные качества атлета влияют несколько факторов, включая возраст, рост и вес. Регрессия пропорционально распределяет меру качества по этим трем факторам на основе его спортивных результатов. Результаты регрессии впоследствии могут быть использованы для предсказания качеств нового, непроверенного атлета.
3. Практическая часть
3.1. Базы данных
Вы являетесь инспектором учебного отдела. Вам необходимо создать базу данных по учету студентов, в которой должны храниться: фамилия и инициалы, № личного дела, специальность, год приема, оценки, полученные на экзаменах и зачетах.
Выходные документы должны обеспечить получение списка студентов, сгруппированного по специальностям и годам приема, а также учетной карточки студента, в которой должны быть отражены оценки, полученные на экзаменах и зачетах (фамилия и инициалы студента вводятся с клавиатуры в момент формирования карточки).
Решение
Согласно заданию, создаем три таблицы при использовании конструктора таблиц, отдельно выделяем таблицу «Предметы».



Создаем схему данных.
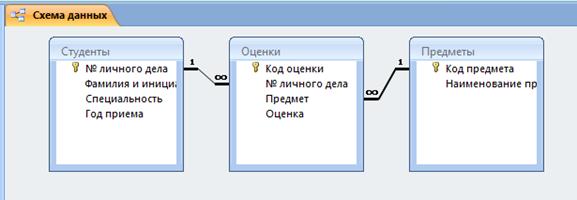
Заполняем таблицы произвольными данными.



Создаем формы при использовании мастера форм для ввода данных.



Запрос



Отчеты


3.2. Электронные таблицы
5. Имеется набор из четырех продуктов, имеющих разную пищевую ценность (калорийность, содержание белков, углеводов, жиров) и цену. Необходимо подобрать оптимальную по цене комбинацию продуктов, обеспечивающую нужную калорийность и учитывающую ограничение (сверху или снизу) на количество белков, жиров, углеводов.
Решение
| Данные | ||||||||||||
| наименьшее содержание белков | ||||||||||||
| наибольшее содержание жиров | ||||||||||||
| наибольшее содержание углеводов | ||||||||||||
| наименьшее содержание углеводов | ||||||||||||
| Общая калорийность | ||||||||||||
| Решение задачи | ||||||||||||
| Составим математическую модель задачи. | ||||||||||||
| Пусть х1,х2,х3,х4- количество продуктов №1,№2,№3,№4 соответственно. | ||||||||||||
| Функция цели: z=8x1+10x2+100x3+70x4 стремится к минимуму | ||||||||||||
| Составим систему ограничений. | ||||||||||||
| 1)Все переменные хi неотрицательные | ||||||||||||
| 2)По калорийности: 29х1+83х2+316х3+226≥1500 | ||||||||||||
| 3)По содержанию белков: 2,1х1+2х2+54,8х3+14х4≥133 | ||||||||||||
| 4) По жирам: 0,1х2+27,8х3+18х4≤88 | ||||||||||||
| 5) По содержанию углеводов:4,9х1+19,7х2+1,3х4≤475 | ||||||||||||
| 4,9х1+19,7х2+1,3х4≥421 | ||||||||||||
| Параметры | продукт №1 | продукт № 2 | продукт № 3 | продукт №4 | ||||||||
| Содержание белков | 2,1 | 54,8 | 153,6 | |||||||||
| Содержание жиров | 0,1 | 27,8 | 57,8 | |||||||||
| Содержание углеводов | 4,9 | 19,7 | 1,3 | 433,4 | ||||||||
| Калорийность | ||||||||||||
| Цена | ||||||||||||
| Количество продуктов | ||||||||||||
| Формулы | F14: "=$B$16*B11+$C$16*C11+$D$16*D11+$E$16*E11" | |||||||||||
| F15: "=$B$19*B15+$C$19*C15+$D$19*D15+$E$19*E15" | ||||||||||||
| F16: "=$B$19*B16+$C$19*C16+$D$19*D16+$E$19*E16" |
| |||||||||||
| F17: "=B17*B19+C19*C17+D19*D17+E19*E17" | ||||||||||||
| F18:"=B18*B19+C18*C19+D18*D19+E18*E19" | ||||||||||||

| ||||||||||||
9. Статистические исследования показали, что местный рынок может поглотить S единиц товара одного и того же назначения, но разных марок Т1, Т2, … Т6. Известна прибыль (D), получаемая от продажи всех S единиц товара каждой марки и общий убыток (U) от невостребованной партии из S единиц товара одной марки. Необходимо спланировать оптимальную структуру закупки партии товара.
.
Решение
В условиях неопределенного поведения проекта конфликтная ситуация поведения рынка формализуется матричной игрой. Пусть первый игрок — рынок, второй игрок — продавец. Каждый из игроков имеет по 6 стратегий. Закупка i-й единицы продукции — i-я. стратегия первого игрока, продажа j единицы продукции— j-я стратегия второго игрока. Тогда матрица выигрышей первого игрока имеет вид квадратной матрицы n-го порядка:

Данная задача является задачей теории игр.
Попробуем решить ее в чистых стратегиях, и если не получится, то в смешанных.
Используем критерии Вальда и Сэвиджа.
Подготовим данные для решения задачи.
Схема решения задачи следующая:
 |
Рис. 1. Схема решения задачи в смешанных стратегиях
с неизвестными вероятностями выбора вариантов
стратегии противником
На рис. 1 платежная матрица дополнена блоком расчета параметров смешанной стратегии. В столбце q поставлены весовые коэффициенты чистых стратегий в смешанной стратегии. Сумма долей S1 должна быть равна 1. Доли не меньше нуля и не больше единицы. При оптимальной стратегии суммы чисел в столбцах максимальны и равны, т.к. являются средними выигрышами игрока А.


| Платежная матрица | min по строке | ||||||||||
| -150 | -150 | -150 | -150 | -150 | -150 | maxmin= | -80 | ||||
| -80 | -80 | -80 | -80 | -80 | -80 | нижняя цена игры | |||||
| -94 | -94 | -94 | -94 | -94 | -94 | ||||||
| -108 | -108 | -108 | -108 | -108 | -108 | ||||||
| -135 | -135 | -135 | -135 | -135 | -135 | ||||||
| -154 | -154 | -154 | -154 | -154 | -154 | ||||||
| max по столбцу | |||||||||||
| minmax= | |||||||||||
| верхняя цена игры | |||||||||||
| Мы видим, что данная задача не разрешима в чистых стратегиях, так как верхняя цена игры не равна нижней. | |||||||||||
| Попробуем решить эту задачу, используя критерий Вальда | |||||||||||
| Предварительные расчеты | |||||||||||
| В1 | В2 | В3 | В4 | В5 | В6 | min по строке | max по строке | ||||
| А1 | -150 | -150 | -150 | -150 | -150 | -150 | |||||
| А2 | -80 | -80 | -80 | -80 | -80 | -80 | |||||
| А3 | -94 | -94 | -94 | -94 | -94 | -94 | |||||
| А4 | -108 | -108 | -108 | -108 | -108 | -108 | |||||
| А5 | -135 | -135 | -135 | -135 | -135 | -135 | |||||
| А6 | -154 | -154 | -154 | -154 | -154 | -154 | |||||
| max по столбцу | |||||||||||
| Находим стратегию, обеспечивающую гарантированный выигрыш игроку А. Для этого находим нижнюю цену игры | |||||||||||
| W = a = max minj aij = -80. Найденный максимум достигается при i=2, т. е., исходя из критерия Вальда, следует осуществлять стратегию А2. | |||||||||||
| Все деньги вложим в проект №2, тогда получим минимальный убыток. | |||||||||||
| Попробуем применить критерий Сэвиджа. |
| Сначала составим матрицу рисков R. | |||||||||
| Для этого определяем максимальные элементы в каждом столбце матрицы | |||||||||
| Затем находим минимум из максимумов по строкам. | minmax= | ||||||||
| Он достигается при стратегии А6. | |||||||||
| То есть нам рекомендуется вложить все деньги в проект № 6, | |||||||||
| тогда в случае удачного исхода у нас будет максимальная прибыль. | |||||||||
| Решаем задачу по схеме. | Денег | ||||||||
| В1 | В2 | В3 | В4 | В5 | В6 | Доля (q) | Количество | ||
| А1 | -150 | -150 | -150 | -150 | -150 | 0,208186244 | 1249,117 | ||
| А2 | -80 | -80 | -80 | -80 | -80 | 0,200179081 | 1201,074 | ||
| А3 | -94 | -94 | -94 | -94 | -94 | 0,174652889 | 1047,917 | ||
| А4 | -108 | -108 | -108 | -108 | -108 | 0,154900479 | 929,4029 | ||
| А5 | -135 | -135 | -135 | -135 | -135 | 0,137568003 | 825,408 | ||
| А6 | -154 | -154 | -154 | -154 | -154 | 0,124513305 | 747,0798 | ||
| Сумма | |||||||||
| В1 | В2 | В3 | В4 | В5 | В6 | ||||
| А1 | 124,9 | -31,23 | -31,2 | -31,23 | -31,2 | -31,23 | |||
| А2 | -16 | 140,1 | -16 | -16,01 | -16 | -16,01 | |||
| А3 | -16,4 | -16,42 | 139,7 | -16,42 | -16,4 | -16,42 | |||
| А4 | -16,7 | -16,73 | -16,7 | 139,4 | -16,7 | -16,73 | |||
| А5 | -18,6 | -18,57 | -18,6 | -18,57 | 137,6 | -18,57 | |||
| А6 | -19,2 | -19,18 | -19,2 | -19,18 | -19,2 | ||||
| Сумма | |||||||||
| Ответ: |
11. Даны два числовых ряда. Качественный анализ показал, что величина Y зависит от величины Х. Необходимо проверить наличие корреляционной линейной зависимости, построить линейное уравнение регрессии и доказать его адекватность.
Исходные данные
| Х | У | УТ=а0+а1х | ε=у-ут | ε2 |
| 10,00 | 35,39 | Ут1 | ε1 | (ε1)2 |
| 20,00 | 21,66 | Ут2 | ε2 | (ε2)2 |
| 30,00 | 3,74 | Ут3 | ε3 | (ε3)2 |
| 40,00 | -11,94 | Ут4 | ε4 | (ε4)2 |
| 50,00 | -25,79 | Ут5 | ε5 | (ε5)2 |
| 60,00 | -38,72 | Ут6 | ε6 | (ε6)2 |
| 70,00 | -55,26 | Ут7 | ε7 | (ε7)2 |
| 80,00 | -71,97 | Ут8 | ε8 | (ε8)2 |
| 90,00 | -83,91 | Ут9 | ε9 | (ε9)2 |
| 100,0 | -103,7 | Ут10 | ε10 | (ε10)2 |
| Σε2 |
Выполнение
Необходимо найти y=F(x)+ε(Случайный остаток)
yТ=F(x)=а0+а1х
Надо найти а0 и а1, ε – отклонение результатов экспериментов от теоретических. Величина каждого отклонения является мерой точности отображения эксперимента с помощью функции F(x).
Σε2-является мерой точности модели. Чем меньше эта сумма, тем лучше модель. Поэтому мы должны подобрать такие а0 и а1, чтобы сумма Σε2 была минимальной.

В качестве средства мы будем использовать приложение «Регрессия» из пакета «Анализ данных».
На рабочем листе создаем таблицу с исходными данными. Оформляем ее с помощью кнопки «Границы» на панели инструментов. В меню Сервис выбираем команду «Анализ данных». В качестве инструмента анализа выбираем «Регрессия» и нажимаем ОК.
Появится окно следующего вида

Вводим входные интервалы Х и У и нажимаем ОК.
Появляется новый лист с таблицами.
| ВЫВОД ИТОГОВ | ||||||||
| Регрессионная статистика | ||||||||
| Множественный R | 0,999422 | |||||||
| R-квадрат | 0,998845 | |||||||
| Нормированный R-квадрат | 0,9987 | |||||||
| Стандартная ошибка | 1,662849 | |||||||
| Наблюдения | ||||||||
| Дисперсионный анализ | ||||||||
| df | SS | MS | F | Значимость F | ||||
| Регрессия | 19125,3 | 19125,3 | 6916,763 | 4,87E-13 | ||||
| Остаток | 22,12052 | 2,765065 | ||||||
| Итого | 19147,42 | |||||||
| Коэффициенты | Стандартная ошибка | t-статистика | P-Значение | Нижние 95% | Верхние 95% | Нижние 95,0% | Верхние 95,0% | |
| Y-пересечение | 50,69133 | 1,135942 | 44,62494 | 7,02E-11 | 48,07185 | 53,31082 | 48,07185 | 53,31082 |
| Переменная X 1 | -1,52257 | 0,018307 | -83,1671 | 4,87E-13 | -1,56479 | -1,48035 | -1,56479 | -1,48035 |
В таблице Регрессионная статистика обращаем внимание на R-квадрат – он показывает наличие корреляционной зависимости. Так как он больше 0,7, то связь между Х и У сильная.
В таблице дисперсионный анализ обратим внимание на значение F. Вычислим табличное значение F для 10 наблюдений используя функцию FРАСПОБР(0,05;1;8).
Сравним два значения, так F расчетное больше F табличного, то модель адекватна.
Из третьей таблицы мы можем найти коэффициенты а0 и а1.
Получаем уравнение у=-1,52х+50,69.
Для того, чтобы проверить значимость коэффициентов а0 и а1, используем столбец «t-статистика» и функцию СТЬЮДРАСПОБР(0,05;9). Вычисляем t-расчетное. Мы видим, что а0 – значим, а а1 – не значим.
Дополним расчеты в таблице.
| Х | У | Утеор | ε | ε2 |
| 35,39 | 35,4656 | -0,0756 | 0,00572 | |
| 21,66 | 20,2399 | 1,42006 | 2,01657 | |
| 3,74 | 5,01424 | -1,2742 | 1,62369 | |
| -11,94 | -10,211 | -1,7285 | 2,98787 | |
| -25,79 | -25,437 | -0,3528 | 0,1245 | |
| -38,72 | -40,663 | 1,94285 | 3,77466 | |
| -55,26 | -55,889 | 0,62855 | 0,39507 | |
| -71,97 | -71,114 | -0,8558 | 0,73232 | |
| -83,91 | -86,34 | 2,42994 | 5,90461 | |
| -103,7 | -101,57 | -2,1344 | 4,55551 | |
| Сумма | 22,12052 |
12. Вам предлагают три варианта помещения денег в различные проекты. Длительность займа одинакова. Предусмотрен разный способ выплаты процентов. Отберите наилучший по эффективности вариант.
| Решение | |||||||
| Заполним таблицу с исходными данными. | |||||||
| Для решения задачи воспользуемся встроенными функциями процессора | |||||||
| Сумма | |||||||
| Периоды | Используемые формулы | ||||||
| варианты | |||||||
| D13: "=БС(C12%;C11;;-B9;0)" | |||||||
| конец | 303 572,58р. | D15: "=БС(C12%;C11;;-B9;1)" | |||||
| D13:"=БЗРАСПИС(B9;C16:C39)" | |||||||
| начало | 303 572,58р. | ||||||
| 0,06 | 297 131,20р. | ||||||
| 0,06 | |||||||
| 0,06 | |||||||
| 0,06 | |||||||
| 0,08 | |||||||
| 0,08 | |||||||
| 0,08 | |||||||
| 0,08 | |||||||
| 0,1 | |||||||
| 0,1 | |||||||
| 0,1 | |||||||
| 0,1 | |||||||
| 0,12 | |||||||
| 0,12 | |||||||
| 0,12 | |||||||
| 0,12 | |||||||
| 0,16 | |||||||
| 0,16 | |||||||
| 0,16 | |||||||
| 0,16 | |||||||
| 0,2 | |||||||
| 0,2 | |||||||
| 0,2 | |||||||
| 0,2 | |||||||
| Эффективны 2 и первый варианты | |||||||
Литература
1. Ершов Б.Л. Программные средства офисного назначения. Учебное пособие. Иваново, 2003
2. Банк В.Р., Зверев В.С. Информационные системы в экономике: Учебник. – М.: Экономист, 2005
3. Ершов Б.Л. Основы информационных технологий в экономике. Учебное пособие. Иваново, 2009
4. Багриновский, К.А. Новые информационные технологии / К.А. Багриновский, Е.Ю. Хрусталев. – М.: ЭКО, 1996. – 229 с.
5. Баронов, В.В. Информационные технологии и управление предприятием / В.В. Баронов, Г.Н., Калянов, Ю.Н. Попов и др. – М.: Компания Айти, 2004. – 328 с.
6. Ватолина М.В. Организация работы с документами / Серия «Высшее образование». – Ростов н/Д: Феникс, 2004. – 320 с.
7. Вендров, А.М. Проектирование программного обеспечения экономических информационных систем / А.М. Вендров. – М., 2000. – 125 с.
8. Гохберг, Г.С. Информационные технологии: учеб. для сред. проф. образ. / Г.С. Гохберг, А.В. Зафиевский, А.А. Короткин. – М.: Издательский центр «Академия», 2004. – 208 с.
9. Демушкин, А.С. Новая терминология в информационных технологиях / А.С. Демушкин // Делопроизводство. – №2. – 2001. – C. 41-48.
10. Зайцев, Н.Г. Принципы информационного обеспечения в системах переработки информации и управления / Н.Г. Зайцев. – Киев, 1976. – 182 с.
11. Захарова, И.Г. Информационные технологии в образовании: учеб. пособие для студ. высш. учеб. зав. / И.Г. Захарова. - 3-е издание стер. – М.: Издательский центр «Академия», 2007. – 192 с.
12. Ибрагимов, И.М. Информационные технологии и средства дистанционного обучения: учеб. пособие для студ. высш. учеб. зав. / И.М. Ибрагимов; под ред. А.Н. Ковшова. – М.:. Издательский центр «Академия», 2005. – 336 с.
13. Кромберг, А.И. Информационное обеспечение управленческой деятельности / А. И. Кромберг // Нар.образ. – 1999. – 65 с.
14. Кудряев, В.А. Организация работы с документами: учеб. / под ред. проф. В.А. Кудряева. - М.: ИНФА-М, 2002. – 592 с.
15. Макарова, Н.В. Информатика: учеб. / Н.В. Макарова, Л.А. Матвеева, В.Л. Пройдо. – М.: Финансы и статистика, 1997. – 383 с.
16. Максимович, Г.Ю., Берестова, В.И Автоматизация информационного обеспечения управления // Секретарское дело. – 2003. - №11. – С. 25-27
17. Максимович, Г.Ю., Берестова, В.И. Современные универсальные информационные технологии – основа совершенствования документационного обеспечения управления // Секретарское дело. - 2005. - №2 – С. 23-27.
18. Могилев, А.В. Информатика: учеб. пособие для студ. высш. пед. учеб. заведений / А.В. Могилев, Е.К. Хеннер, Н.И. Пак; под ред. А.В. Могилева. – М.: Изд. Центр «Академия», 2006. – 336 с.
19. Пшенко А.В. Делопроизводство: документационное обеспечение работы офиса: учеб. пособие для студ. учр. сред. проф. образ. / А.В. Пшенко. – М.: Мастерство, 2000. – 176 с.
20. Семенов, М.И. Информатизированные информационные технологии в экономике: учеб. / М. И. Семенов, И.Т. Трубилин, В.И. Лойко, Г.П. Барановская; под общ. ред. И.Т. Трубилина. – М.: Финансы и статистика, 2000. – 416 с.
21. Симонович, С.В. Информатика. Базовый курс / под ред. С.В. Симоновича. – 2-е изд. – СПб.: Питер, 2003. – 640 с.
22. Титоренко, Г.А. Автоматизированные информационные технологии в экономике: учеб. / под ред. Г.А. Титоренко. – М.: Юнити, 2006. – 399 с.
23. Титоренко, Г.А. Информационные технологии управления: уч. пособие для вузов / под ред. Г. А. Титоренко. – 2-е изд., доп. – М.: Юнита-Дана, 2005. – 439 с.
24. Хомоненко А.Д. Основы современных компьютерных технологий: учеб. / под ред. проф. А.Д. Хомоненко. – СПб: КОРОНА принт, 2005. – 672 с.
Поиск по сайту: