 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Открытия будущего
ЛИТЕРАТУРА
1. Турчак Л.И., Плотников П.В. Основы численных методов. – М.: Физматлит, 2002.
2. Численные методы / Лапчик М.П., Рагулина М.И., Хеннер Е.К. М.: Издат. центр «Академия», 2004.
3. Приближенное решение нелинейных уравнений: Метод. указания / КХТИ. Сост. А.В. Садыков, Казань, 1991.
4. Некоторые методы решения задачи аппроксимации: Метод. указания / Казан. гос. технол. ун-т. Сост. А.Г. Багоутдинова, Т.А. Хрузина, Казань, 2000.
Вариант 2
1. Отделить корни уравнения графически и уточнить один из них методом касательных с точностью 
=0,001.
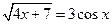
2. Решить систему нелинейных уравнений методом Ньютона с точностью 
. Начальное приближение определить графическим способом.
3. Решить систему линейных уравнений с трехдиагональной матрицей методом прогонки
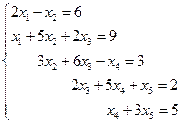
4. Решить систему линейных уравнений методом Зейделя с точностью .
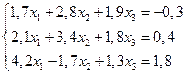
5. Функция задана таблично:
| 1,5 | 2,5 | |||
| 0,2 | 1,8 | 2,4 | 2,2 |
Построить интерполяционный полином Лагранжа для этой функции. С помощью этого полинома найти приближенное значение функции в точке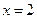 
.
6. Построить интерполяционный полином Ньютона для функции, заданной таблично:
|
| 0,1 | 0,5 | 0,9 | 1,3 | 1,7 |
|
| 1,3 | 1,7 | 2,8 | 3,2 | 2,9 |
С помощью этого полинома найти приближенное значение функции при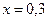 
.
7. Вычислить определенный интеграл методами прямоугольников, трапеций и парабол при 
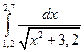
8. Функция задана таблично
|
| 0,5 | 1,5 | 4,5 | ||||
|
| 2,61 | 5,49 | 7,02 | 10,10 | 13,11 | 14,6 | 16,12 |
Построить аппроксимирующую прямую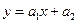 
, используя метод наименьших квадратов (решить сначала вручную, затем с помощью программы).
9. Дана задача Коши для обыкновенного дифференциального уравнения I порядка:
(
– номер варианта)
Найти численное решение задачи методами Эйлера и Рунге-Кутта при .
10. Найти численное решение краевой задачи
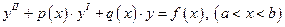
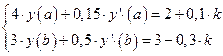
методом конечных разностей
а) вручную: при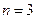 
;
б) с помощью программы: при 
.
Здесь
; 
; 
; 
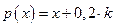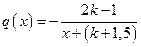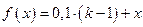
; – номер варианта
ЛИТЕРАТУРА
1. Турчак Л.И., Плотников П.В. Основы численных методов. – М.: Физматлит, 2002.
2. Численные методы / Лапчик М.П., Рагулина М.И., Хеннер Е.К. М.: Издат. центр «Академия», 2004.
3. Приближенное решение нелинейных уравнений: Метод. указания / КХТИ. Сост. А.В. Садыков, Казань, 1991.
4. Некоторые методы решения задачи аппроксимации: Метод. указания / Казан. гос. технол. ун-т. Сост. А.Г. Багоутдинова, Т.А. Хрузина, Казань, 2000.
Вариант 3
1. Отделить корни уравнения графически и уточнить один из них методом итераций с точностью =0,001.
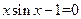
2. Решить систему нелинейных уравнений методом Ньютона с точностью . Начальное приближение определить графическим способом.
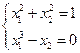
3. Решить систему линейных уравнений с трехдиагональной матрицей методом прогонки
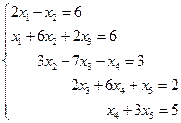
4. Решить систему линейных уравнений методом Зейделя с точностью .
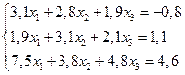
5. Функция задана таблично:
|
| 0,5 | 1,5 | |||
|
| 0,4 | 0,8 | 1,7 | 2,6 | 2,4 |
Построить интерполяционный полином Лагранжа для этой функции. С помощью этого полинома найти приближенное значение функции в точке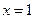 
.
6. Построить интерполяционный полином Ньютона для функции, заданной таблично:
|
| 0,1 | 0,3 | 0,5 | 0,7 | 0,9 |
|
| 2,4 | 2,8 | 3,4 | 3,9 | 3,7 |
С помощью этого полинома найти приближенное значение функции при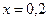 
.
7. Вычислить определенный интеграл методами прямоугольников, трапеций и парабол при
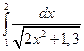
8. Функция задана таблично
|
| 1,5 | 4,5 | |||||
|
| 1,91 | 3,12 | 5,91 | 8,11 | 9,10 | 10,11 | 12,10 |
Построить аппроксимирующую прямую 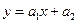, используя метод наименьших квадратов (решить сначала вручную, затем с помощью программы).
9. Дана задача Коши для обыкновенного дифференциального уравнения I порядка:
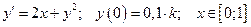( – номер варианта)
Найти численное решение задачи методами Эйлера и Рунге-Кутта при .
10. Найти численное решение краевой задачи
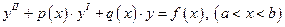
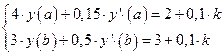
методом конечных разностей
а) вручную: при ;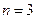
б) с помощью программы: при .
Здесь
; ;
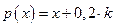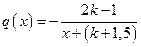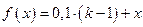
; ; – номер варианта
ЛИТЕРАТУРА
1. Турчак Л.И., Плотников П.В. Основы численных методов. – М.: Физматлит, 2002.
2. Численные методы / Лапчик М.П., Рагулина М.И., Хеннер Е.К. М.: Издат. центр «Академия», 2004.
3. Приближенное решение нелинейных уравнений: Метод. указания / КХТИ. Сост. А.В. Садыков, Казань, 1991.
4. Некоторые методы решения задачи аппроксимации: Метод. указания / Казан. гос. технол. ун-т. Сост. А.Г. Багоутдинова, Т.А. Хрузина, Казань, 2000.
Вариант 4
1. Отделить корни уравнения графически и уточнить один из них методом касательных с точностью =0,001.
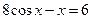
2. Решить систему нелинейных уравнений методом Ньютона с точностью . Начальное приближение определить графическим способом.
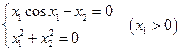
3. Решить систему линейных уравнений с трехдиагональной матрицей методом прогонки
4. Решить систему линейных уравнений методом Зейделя с точностью .
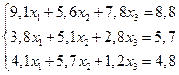
5. Функция задана таблично:
|
| 1,5 | 2,4 | 4,5 | ||
|
| 1,7 | 2,6 | 3,2 | 3,8 | 3,7 |
Построить интерполяционный полином Лагранжа для этой функции. С помощью этого полинома найти приближенное значение функции в точке .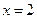
6. Построить интерполяционный полином Ньютона для функции, заданной таблично:
|
| 0,2 | 0,4 | 0,6 | 0,8 | 1,0 |
|
| 2,1 | 2,5 | 3,1 | 3,9 | 3,7 |
С помощью этого полинома найти приближенное значение функции при .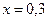
7. Вычислить определенный интеграл методами прямоугольников, трапеций и парабол при
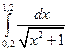
8. Функция задана таблично
|
| 2,5 | 5,5 | |||||
|
| 3,9 | 4,91 | 5,89 | 7,95 | 9,90 | 10,94 | 11,86 |
Построить аппроксимирующую прямую 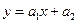, используя метод наименьших квадратов (решить сначала вручную, затем с помощью программы).
9. Дана задача Коши для обыкновенного дифференциального уравнения I порядка:
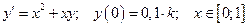( – номер варианта)
Найти численное решение задачи методами Эйлера и Рунге-Кутта при .
10. Найти численное решение краевой задачи
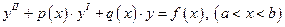
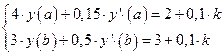
методом конечных разностей
а) вручную: при ;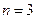
б) с помощью программы: при .
Здесь
; ;
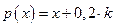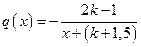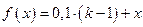
; ; – номер варианта
ЛИТЕРАТУРА
1. Турчак Л.И., Плотников П.В. Основы численных методов. – М.: Физматлит, 2002.
2. Численные методы / Лапчик М.П., Рагулина М.И., Хеннер Е.К. М.: Издат. центр «Академия», 2004.
3. Приближенное решение нелинейных уравнений: Метод. указания / КХТИ. Сост. А.В. Садыков, Казань, 1991.
4. Некоторые методы решения задачи аппроксимации: Метод. указания / Казан. гос. технол. ун-т. Сост. А.Г. Багоутдинова, Т.А. Хрузина, Казань, 2000.
Вариант 5
1. Отделить корни уравнения графически и уточнить один из них методом итераций с точностью =0,001.
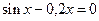
2. Решить систему нелинейных уравнений методом Ньютона с точностью . Начальное приближение определить графическим способом.
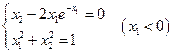
3. Решить систему линейных уравнений с трехдиагональной матрицей методом прогонки
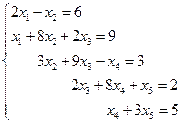
4. Решить систему линейных уравнений методом Зейделя с точностью .
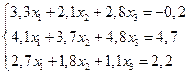
5. Функция задана таблично:
|
| 0,4 | 1,6 | 2,5 | ||
|
| -0,1 | 0,5 | 1,8 | 2,9 | 2,6 |
Построить интерполяционный полином Лагранжа для этой функции. С помощью этого полинома найти приближенное значение функции в точке .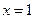
6. Построить интерполяционный полином Ньютона для функции, заданной таблично:
|
| 0,4 | 0,6 | 0,8 | 1,0 | 1,2 |
|
| 2,3 | 2,8 | 3,4 | 4,2 | 3,9 |
С помощью этого полинома найти приближенное значение функции при 
.
7. Вычислить определенный интеграл методами прямоугольников, трапеций и парабол при
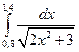
8. Функция задана таблично
|
| 2,5 | 3,5 | 4,1 | ||||
|
| 2,91 | 5,92 | 7,41 | 8,92 | 7,41 | 12,11 | 14,85 |
Построить аппроксимирующую прямую 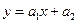, используя метод наименьших квадратов (решить сначала вручную, затем с помощью программы).
9. Дана задача Коши для обыкновенного дифференциального уравнения I порядка:
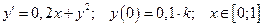( – номер варианта)
Найти численное решение задачи методами Эйлера и Рунге-Кутта при .
10. Найти численное решение краевой задачи
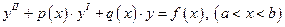
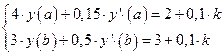
методом конечных разностей
а) вручную: при ;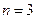
б) с помощью программы: при .
Здесь
; ;
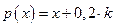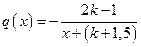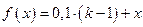
; ; – номер варианта
ЛИТЕРАТУРА
1. Турчак Л.И., Плотников П.В. Основы численных методов. – М.: Физматлит, 2002.
2. Численные методы / Лапчик М.П., Рагулина М.И., Хеннер Е.К. М.: Издат. центр «Академия», 2004.
3. Приближенное решение нелинейных уравнений: Метод. указания / КХТИ. Сост. А.В. Садыков, Казань, 1991.
4. Некоторые методы решения задачи аппроксимации: Метод. указания / Казан. гос. технол. ун-т. Сост. А.Г. Багоутдинова, Т.А. Хрузина, Казань, 2000.
Вариант 6
1. Отделить корни уравнения графически и уточнить один из них методом касательных с точностью =0,001.
2. Решить систему нелинейных уравнений методом Ньютона с точностью . Начальное приближение определить графическим способом.
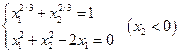
3. Решить систему линейных уравнений с трехдиагональной матрицей методом прогонки
4. Решить систему линейных уравнений методом Зейделя с точностью .
5. Функция задана таблично:
|
| 0,6 | 1,5 | 2,1 | ||
|
| 0,9 | 1,4 | 2,6 | 3,2 | 2,9 |
Построить интерполяционный полином Лагранжа для этой функции. С помощью этого полинома найти приближенное значение функции в точке .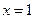
6. Построить интерполяционный полином Ньютона для функции, заданной таблично:
|
| 0,4 | 0,6 | 0,8 | 1,0 | 1,2 |
|
| 5,5 | 5,9 | 5,1 | 4,8 | 3,9 |
С помощью этого полинома найти приближенное значение функции при .
7. Вычислить определенный интеграл методами прямоугольников, трапеций и парабол при
8. Функция задана таблично
|
| 0,5 | 2,5 | 3,5 | ||||
|
| 1,21 | 2,15 | 4,21 | 5,12 | 6,11 | 7,15 | 8,21 |
Построить аппроксимирующую прямую 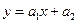, используя метод наименьших квадратов (решить сначала вручную, затем с помощью программы).
9. Дана задача Коши для обыкновенного дифференциального уравнения I порядка:
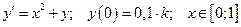( – номер варианта)
Найти численное решение задачи методами Эйлера и Рунге-Кутта при .
10. Найти численное решение краевой задачи
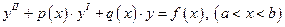
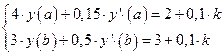
методом конечных разностей
а) вручную: при ;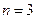
б) с помощью программы: при .
Здесь
; ;
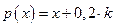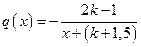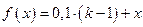
; ; – номер варианта
ЛИТЕРАТУРА
1. Турчак Л.И., Плотников П.В. Основы численных методов. – М.: Физматлит, 2002.
2. Численные методы / Лапчик М.П., Рагулина М.И., Хеннер Е.К. М.: Издат. центр «Академия», 2004.
3. Приближенное решение нелинейных уравнений: Метод. указания / КХТИ. Сост. А.В. Садыков, Казань, 1991.
4. Некоторые методы решения задачи аппроксимации: Метод. указания / Казан. гос. технол. ун-т. Сост. А.Г. Багоутдинова, Т.А. Хрузина, Казань, 2000.
Вариант 7
1. Отделить корни уравнения графически и уточнить один из них методом итераций точностью =0,001.
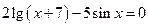
2. Решить систему нелинейных уравнений методом Ньютона с точностью . Начальное приближение определить графическим способом.
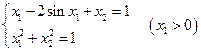
3. Решить систему линейных уравнений с трехдиагональной матрицей методом прогонки
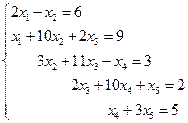
4. Решить систему линейных уравнений методом Зейделя с точностью .
5. Функция задана таблично:
|
| 0,2 | 1,2 | 2,5 | ||
|
| 0,7 | 1,1 | 1,9 | 1,5 | 0,9 |
Построить интерполяционный полином Лагранжа для этой функции. С помощью этого полинома найти приближенное значение функции в точке .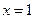
6. Построить интерполяционный полином Ньютона для функции, заданной таблично:
|
| 0,1 | 0,3 | 0,5 | 0,7 | 0,9 |
|
| 1,8 | 2,3 | 2,8 | 3,7 | 3,2 |
С помощью этого полинома найти приближенное значение функции при .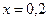
7. Вычислить определенный интеграл методами прямоугольников, трапеций и парабол при
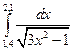
8. Функция задана таблично
|
| 0,5 | 1,5 | 2,5 | 4,5 | |||
|
| 1,31 | 3,28 | 4,25 | 5,31 | 6,29 | 8,26 | 9,21 |
Построить аппроксимирующую прямую 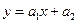, используя метод наименьших квадратов (решить сначала вручную, затем с помощью программы).
9. Дана задача Коши для обыкновенного дифференциального уравнения I порядка:
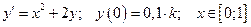( – номер варианта)
Найти численное решение задачи методами Эйлера и Рунге-Кутта при .
10. Найти численное решение краевой задачи
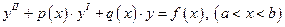
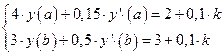
методом конечных разностей
а) вручную: при ;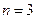
б) с помощью программы: при .
Здесь
; ;
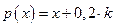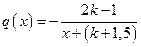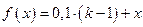
; ; – номер варианта
ЛИТЕРАТУРА
1. Турчак Л.И., Плотников П.В. Основы численных методов. – М.: Физматлит, 2002.
2. Численные методы / Лапчик М.П., Рагулина М.И., Хеннер Е.К. М.: Издат. центр «Академия», 2004.
3. Приближенное решение нелинейных уравнений: Метод. указания / КХТИ. Сост. А.В. Садыков, Казань, 1991.
4. Некоторые методы решения задачи аппроксимации: Метод. указания / Казан. гос. технол. ун-т. Сост. А.Г. Багоутдинова, Т.А. Хрузина, Казань, 2000.
Вариант 8
1. Отделить корни уравнения графически и уточнить один из них методом касательных с точностью =0,001.
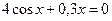
2. Решить систему нелинейных уравнений методом Ньютона с точностью . Начальное приближение определить графическим способом.
3. Решить систему линейных уравнений с трехдиагональной матрицей методом прогонки
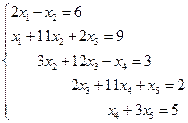
4. Решить систему линейных уравнений методом Зейделя с точностью .
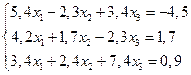
5. Функция задана таблично:
|
| 0,4 | 1,4 | 2,5 | ||
|
| 4,1 | 3,2 | 3,8 | 4,3 | 5,2 |
Построить интерполяционный полином Лагранжа для этой функции. С помощью этого полинома найти приближенное значение функции в точке .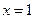
6. Построить интерполяционный полином Ньютона для функции, заданной таблично:
|
| 0,1 | 0,5 | 0,9 | 1,3 | 1,7 |
|
| 2,2 | 2,8 | 3,7 | 4,2 | 3,9 |
С помощью этого полинома найти приближенное значение функции при .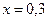
7. Вычислить определенный интеграл методами прямоугольников, трапеций и парабол при
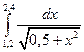
8. Функция задана таблично
|
| 1,5 | 4,5 | |||||
|
| 2,31 | 3,35 | 4,28 | 6,31 | 8,29 | 9,21 | 10,32 |
Построить аппроксимирующую прямую 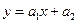, используя метод наименьших квадратов (решить сначала вручную, затем с помощью программы).
9. Дана задача Коши для обыкновенного дифференциального уравнения I порядка:
( – номер варианта)
Найти численное решение задачи методами Эйлера и Рунге-Кутта при .
10. Найти численное решение краевой задачи
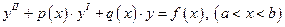
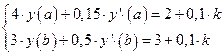
методом конечных разностей
а) вручную: при ;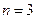
б) с помощью программы: при .
Здесь
; ;
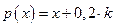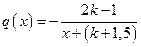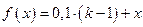
; ; – номер варианта
ЛИТЕРАТУРА
1. Турчак Л.И., Плотников П.В. Основы численных методов. – М.: Физматлит, 2002.
2. Численные методы / Лапчик М.П., Рагулина М.И., Хеннер Е.К. М.: Издат. центр «Академия», 2004.
3. Приближенное решение нелинейных уравнений: Метод. указания / КХТИ. Сост. А.В. Садыков, Казань, 1991.
4. Некоторые методы решения задачи аппроксимации: Метод. указания / Казан. гос. технол. ун-т. Сост. А.Г. Багоутдинова, Т.А. Хрузина, Казань, 2000.
Вариант 9
1. Отделить корни уравнения графически и уточнить один из них методом итераций с точностью =0,001.
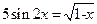
2. Решить систему нелинейных уравнений методом Ньютона с точностью . Начальное приближение определить графическим способом.
3. Решить систему линейных уравнений с трехдиагональной матрицей методом прогонки
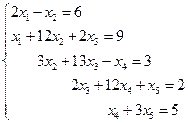
4. Решить систему линейных уравнений методом Зейделя с точностью .
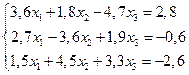
5. Функция задана таблично:
|
| 0,6 | 1,5 | 2,1 | ||
|
| -3 | -2,4 | 0,2 | 0,7 | 0,6 |
Построить интерполяционный полином Лагранжа для этой функции. С помощью этого полинома найти приближенное значение функции в точке .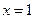
6. Построить интерполяционный полином Ньютона для функции, заданной таблично:
|
| 0,2 | 0,4 | 0,6 | 0,8 | 1,0 |
|
| 2,2 | 2,9 | 3,8 | 4,1 | 3,9 |
С помощью этого полинома найти приближенное значение функции при .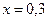
7. Вычислить определенный интеграл методами прямоугольников, трапеций и парабол при
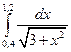
8. Функция задана таблично
|
| 0,5 | 1,4 | 2,5 | 3,4 | |||
|
| 1,61 | 4,31 | 6,02 | 7,58 | 9,08 | 10,25 | 12,19 |
Построить аппроксимирующую прямую 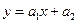, используя метод наименьших квадратов (решить сначала вручную, затем с помощью программы).
9. Дана задача Коши для обыкновенного дифференциального уравнения I порядка:
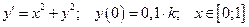( – номер варианта)
Найти численное решение задачи методами Эйлера и Рунге-Кутта при .
10. Найти численное решение краевой задачи
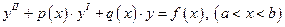
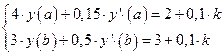
методом конечных разностей
а) вручную: при ;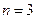
б) с помощью программы: при .
Здесь
; ;
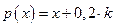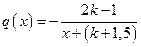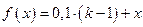
; ; – номер варианта
ЛИТЕРАТУРА
1. Турчак Л.И., Плотников П.В. Основы численных методов. – М.: Физматлит, 2002.
2. Численные методы / Лапчик М.П., Рагулина М.И., Хеннер Е.К. М.: Издат. центр «Академия», 2004.
3. Приближенное решение нелинейных уравнений: Метод. указания / КХТИ. Сост. А.В. Садыков, Казань, 1991.
4. Некоторые методы решения задачи аппроксимации: Метод. указания / Казан. гос. технол. ун-т. Сост. А.Г. Багоутдинова, Т.А. Хрузина, Казань, 2000.
Вариант 10
1. Отделить корни уравнения графически и уточнить один из них методом касательных с точностью =0,001.
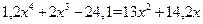
2. Решить систему нелинейных уравнений методом Ньютона с точностью . Начальное приближение определить графическим способом.
3. Решить систему линейных уравнений с трехдиагональной матрицей методом прогонки
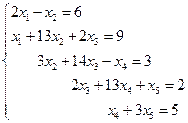
4. Решить систему линейных уравнений методом Зейделя с точностью .
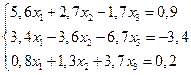
5. Функция задана таблично:
|
| 0,4 | 1,5 | |||
|
| 0,8 | 1,9 | 2,7 | 3,2 | 2,9 |
Построить интерполяционный полином Лагранжа для этой функции. С помощью этого полинома найти приближенное значение функции в точке .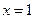
6. Построить интерполяционный полином Ньютона для функции, заданной таблично:
|
| 0,1 | 0,3 | 0,5 | 0,7 | 0,9 |
|
| 2,2 | 2,8 | 3,5 | 4,3 | 4,1 |
С помощью этого полинома найти приближенное значение функции при .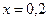
7. Вычислить определенный интеграл методами прямоугольников, трапеций и парабол при
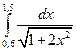
8. Функция задана таблично
|
| 1,2 | 2,1 | 2,5 | 3,5 | |||
|
| 2,5 | 4,3 | 5,1 | 6,1 | 7,2 | 8,15 | 10,1 |
Построить аппроксимирующую прямую 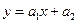, используя метод наименьших квадратов (решить сначала вручную, затем с помощью программы).
9. Дана задача Коши для обыкновенного дифференциального уравнения I порядка:
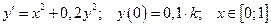( – номер варианта)
Найти численное решение задачи методами Эйлера и Рунге-Кутта при .
10. Найти численное решение краевой задачи
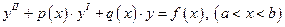
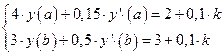
методом конечных разностей
а) вручную: при ;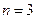
б) с помощью программы: при .
Здесь
; ;
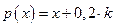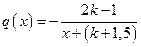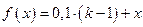
; ; – номер варианта
ЛИТЕРАТУРА
1. Турчак Л.И., Плотников П.В. Основы численных методов. – М.: Физматлит, 2002.
2. Численные методы / Лапчик М.П., Рагулина М.И., Хеннер Е.К. М.: Издат. центр «Академия», 2004.
3. Приближенное решение нелинейных уравнений: Метод. указания / КХТИ. Сост. А.В. Садыков, Казань, 1991.
4. Некоторые методы решения задачи аппроксимации: Метод. указания / Казан. гос. технол. ун-т. Сост. А.Г. Багоутдинова, Т.А. Хрузина, Казань, 2000.
Вариант 11
1. Отделить корни уравнения графически и уточнить один из них методом итераций с точностью =0,001.
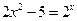
2. Решить систему нелинейных уравнений методом Ньютона с точностью . Начальное приближение определить графическим способом.
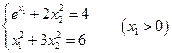
3. Решить систему линейных уравнений с трехдиагональной матрицей методом прогонки
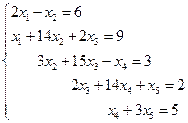
4. Решить систему линейных уравнений методом Зейделя с точностью .
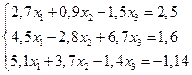
5. Функция задана таблично:
|
| 0,3 | 1,5 | |||
|
| 0,1 | 0,7 | 1,4 | 2,1 | 1,9 |
Построить интерполяционный полином Лагранжа для этой функции. С помощью этого полинома найти приближенное значение функции в точке .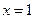
6. Построить интерполяционный полином Ньютона для функции, заданной таблично:
|
| 0,2 | 0,4 | 0,6 | 0,8 | |
|
| 3,4 | 4,1 | 4,9 | 5,8 | 5,6 |
С помощью этого полинома найти приближенное значение функции при .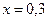
7. Вычислить определенный интеграл методами прямоугольников, трапеций и парабол при
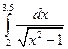
8. Функция задана таблично
|
| 1,5 | 4,5 | |||||
|
| 2,9 | 4,4 | 5,9 | 8,9 | 11,9 | 13,4 | 14,8 |
Построить аппроксимирующую прямую 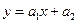, используя метод наименьших квадратов (решить сначала вручную, затем с помощью программы).
9. Дана задача Коши для обыкновенного дифференциального уравнения I порядка:
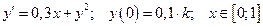( – номер варианта)
Найти численное решение задачи методами Эйлера и Рунге-Кутта при .
10. Найти численное решение краевой задачи
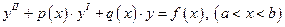
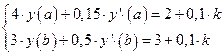
методом конечных разностей
а) вручную: при ;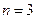
б) с помощью программы: при .
Здесь
; ;
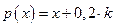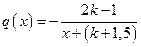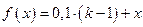
; ; – номер варианта
ЛИТЕРАТУРА
1. Турчак Л.И., Плотников П.В. Основы численных методов. – М.: Физматлит, 2002.
2. Численные методы / Лапчик М.П., Рагулина М.И., Хеннер Е.К. М.: Издат. центр «Академия», 2004.
3. Приближенное решение нелинейных уравнений: Метод. указания / КХТИ. Сост. А.В. Садыков, Казань, 1991.
4. Некоторые методы решения задачи аппроксимации: Метод. указания / Казан. гос. технол. ун-т. Сост. А.Г. Багоутдинова, Т.А. Хрузина, Казань, 2000.
Вариант 12
1. Отделить корни уравнения графически и уточнить один из них методом касательных с точностью =0,001.
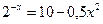
2. Решить систему нелинейных уравнений методом Ньютона с точностью . Начальное приближение определить графическим способом.
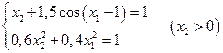
3. Решить систему линейных уравнений с трехдиагональной матрицей методом прогонки
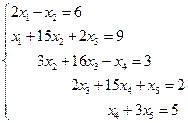
4. Решить систему линейных уравнений методом Зейделя с точностью .
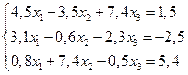
5. Функция задана таблично:
|
| 0,6 | 1,5 | 2,5 | ||
|
| 0,2 | 0,8 | 1,5 | 3,1 | 2,8 |
Построить интерполяционный полином Лагранжа для этой функции. С помощью этого полинома найти приближенное значение функции в точке .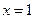
6. Построить интерполяционный полином Ньютона для функции, заданной таблично:
|
| 0,2 | 0,4 | 0,6 | 0,8 | |
|
| 3,5 | 2,8 | 2,2 | 1,9 | 2,3 |
С помощью этого полинома найти приближенное значение функции при .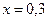
7. Вычислить определенный интеграл методами прямоугольников, трапеций и парабол при
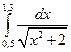
8. Функция задана таблично
Поиск по сайту: