 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
ВАЛЫ И ОСИ
Колёса передач установлены на специальных продолговатых деталях круглого сечения. Среди таких деталей различают оси и валы.
Ось – деталь, служащая для удержания колёс и центрирования их вращения. Вал – ось, передающая вращающий момент.
Не следует путать понятия "ось колеса", это деталь и "ось вращения", это геометрическая линия центров вращения.
Формы валов и осей весьма многообразны от простейших цилиндров до сложных коленчатых конструкций. Известны конструкции гибких валов, которые 
предложил шведский инженер Карл де Лаваль ещё в 1889 г.
Форма вала определяется распределением изгибающих и крутящих моментов по его длине. Правильно спроектированный вал представляет собой балку равного сопротивления.
Валы и оси вращаются, а следовательно, испытывают знакопеременные на
 |
грузки, напряжения и деформации. Поэтому поломки валов и осей имеют усталостный характер.
Причины поломок валов и осей прослеживаются на всех этапах их "жизни".
1. На стадии проектирования – неверный выбор формы, неверная оценка концентраторов напряжений.
2. На стадии изготовления – надрезы, забоины, вмятины от небрежного обращения.
3. На стадии эксплуатации – неверная регулировка подшипниковых узлов.
Для работоспособности вала или оси необходимо обеспечить:
объёмную прочность (способность сопротивляться Mизг и Мкрут);
поверхностную прочность (особенно в местах соединения с другими деталями);
жёсткость на изгиб;
крутильную жёсткость (особенно для длинных валов).
Все валы в обязательном порядке рассчитывают на объёмную прочность.
Схемы нагружения валов и осей зависят от количества и места установки на них вращающихся деталей и направления действия сил. При сложном нагружении выбирают две ортогональные плоскости (например, фронтальную и горизонтальную) и рассматривают схему в каждой плоскости. Рассчитываются, конечно, не реальные конструкции, а упрощённые расчётные модели, представляющие собой балки на шарнирных опорах, балки с заделкой и даже статически неопределимые задачи.
При составлении расчётной схемы валы рассматривают как прямые брусья, лежащие на шарнирных опорах. При выборе типа опоры полагают, что деформации валов малы и, если подшипник допускает хотя бы небольшой наклон или перемещение цапфы, его считают шарнирно-неподвижной или шарнирно-подвижной опорой. Подшипники скольжения или качения, воспринимающие одновременно радиальные и осевые усилия, рассматривают как шарнирно-неподвижные опоры, а подшипники, воспринимающие только радиальные усилия, - как шарнирно-подвижные.
Такие задачи хорошо известны студентам из курсов теоретической механики (статики) и сопротивления материалов.
Расчёт вала на объёмную прочность выполняют в три этапа.
I. Предварительный расчёт валов
Выполняется на стадии проработки Технического Задания, когда известны только вращающие моменты на всех валах машины. При этом считается, что вал испытывает только касательные напряжения кручения
tкр = Мвр / Wp £ [ t ] кр,
где Wp - полярный момент сопротивления сечения.
Для круглого сечения: Wp = pd3/16, [ t ] кр= 15 ¸ 20 Н/мм2.
Условие прочности по напряжениям кручения удобно решать относительно диаметра вала
.
Это – минимальный диаметр вала. На всех других участках вала он может быть только больше. Вычисленный минимальный диаметр вала округляется до ближайшего большего из нормального ряда. Этот диаметр является исходным для дальнейшего проектирования.
II. Уточнённый расчёт валов
На данном этапе учитывает не только вращающий, но и изгибающие моменты. Выполняется на этапе эскизной компоновки, когда предварительно выбраны подшипники, известна длина всех участков вала, известно положение всех колёс на валу, рассчитаны силы, действующие на вал.
Чертятся расчётные схемы вала в двух плоскостях. По известным силам в зубчатых передачах и расстояниям до опор строятся эпюры изгибающих моментов в горизонтальной и фронтальной плоскостях. Затем вычисляется суммарный изгибающий момент
Далее рассчитывается и строится эпюра эквивалентного "изгибающе-вращающего" момента
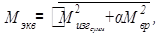
где α = 0,75 или 1 в зависимости от принятой энергетической теории прочности [5], принимаемый большинством авторов равным 1.
Вычисляется эквивалентное напряжение от совместного действия изгиба и кручения s экв = Мэкв / Wp.
Уравнение также решается относительно минимального диаметра вала
Или то же самое для сравнения с допускаемыми нормальными напряжениями:
Полученный в уточнённом расчёте минимальный диаметр вала принимается окончательно для дальнейшего проектирования.
III. Расчёт вала на выносливость
Выполняется как проверочный на стадии рабочего проектирования, когда практически готов рабочий чертёж вала, т.е. известна его точная форма, размеры и все концентраторы напряжений: шпоночные пазы, кольцевые канавки, сквозные и глухие отверстия, посадки с натягом, галтели (плавные, скруглённые переходы диаметров).
При расчёте полагается, что напряжения изгиба изменяются по симметричному циклу, а касательные напряжения кручения – по отнулевому пульсирующему циклу.
Проверочный расчёт вала на выносливость по существу сводится к определению фактического коэффициента запаса прочности n, который сравнивается с допускаемым
Здесь ns и nt - коэффициенты запаса по нормальным и касательным напряжениям
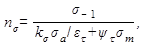
где s -1 и τ-1 – пределы выносливости материала вала при изгибе и кручении с симметричным циклом; kσ и kτ – эффективные коэффициенты концентрации напряжений при изгибе и кручении, учитывающие галтели, шпоночные канавки, прессовые посадки и резьбу; εα и ετ – масштабные коэффициенты диаметра вала; s a и τa – амплитудные значения напряжений; s m и τm – средние напряжения цикла (s m = 0, τm = τa); ψσ и ψτ – коэффициенты влияния среднего напряжения цикла на усталостную прочность зависят от типа стали.
Вычисление коэффициентов запаса прочности по напряжениям подробно излагалось в курсе "Сопротивление материалов", в разделе "Циклическое напряжённое состояние".
Если коэффициент запаса оказывается меньше требуемого, то сопротивление усталости можно существенно повысить, применив поверхностное упрочнение: азотирование, поверхностную закалку токами высокой частоты, дробеструйный наклёп, обкатку роликами и т.д. При этом можно получить увеличение предела выносливости до 50% и более.
Силы в зубчатом зацеплении
Фактически, движение передаётся зубчатым зацеплением посредством силы нормального давления в точке контакта зубьев Fn, которая определяется, как интеграл от контактных напряжений s к по всей площади S контакта зубьев Fn = ∫s ( s к )d S.
Однако этот интеграл вычислить практически невозможно, т.к. неизвестен точный вид функции s к.
Используют другой приём: ещё неизвестную силу нормального давления Fn сначала раскладывают на три ортогональных проекции:
осевую силу Fa, направленную параллельно оси колеса;
è радиальную силу Fr, направленную по радиусу к центру колеса;
è окружную силу Ft, направленную касательно к делительной окружности.
Легче всего вычислить силу Ft, зная передаваемый вращающий момент Мвр и делительный диаметр dw
Ft = 2MВр / dw.
Радиальная сила вычисляется, зная угол зацепления aw
Fr = Ft tgaw.
Осевая сила вычисляется через окружную силу и угол наклона зубьев b
Fa = Ft tgb.
Наконец, если необходимо, зная все проекции, можно вычислить и модуль нормальной силы Fn= ( Fa2 + Fr2 + Ft2 ) ½ = Ft / ( cosαw cosβ ).
Нормальная сила распределена по длине контактной линии, поэтому, зная длину lS контактной линии,можно вычислить удельную погонную нормальную нагрузку qn = Fn / lΣ ≈ Ft / ( b εαkε cosαw cosβ ),
где e a - коэффициент перекрытия, k e - отношение минимальной длины контактной линии к средней.
Для двух цилиндрических колёс в зацеплении одноимённые силы равны, но противоположны. Окружная сила для шестерни противоположна направлению вращения, окружная сила для колеса направлена в сторону вращения.
Расчёт зубьев на контактную выносливость
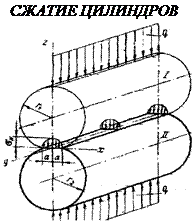Аналитическими методами теории прочности можно получить точное решение для вычисления напряжений в контакте двух эвольвентных профилей. Однако это слишком усложнит задачу, поэтому на малой площадке контакта геометрия эвольвентных профилей корректно подменяется контактом двух цилиндров. Для этого случая используют формулу Герца-Беляева:
Здесь Епр – приведённый модуль упругости материалов шестерни и колеса
Епр = 2 Е1 Е2 / ( Е1 + Е2 ),
rпр – приведённый радиус кривизны зубьев
1/rпр = 1/r1 ± 1/r2, r1,2 = 0,5dW 1,2 sin aW,
n - коэффициент Пуассона, qn - удельная погонная нормальная нагрузка, [ s ] HE - допускаемые контактные напряжения с учётом фактических условий работы.
Расчёт зубьев на контактную выносливость для закрытых передач (длительно работают на постоянных режимах без перегрузок) выполняют как проектировочный. В расчёте задаются передаточным отношением, которое зависит от делительных диаметров и определяют межосевое расстояние Аw (или модуль m), а через него и все геометрические параметры зубьев. Для открытых передач контактные дефекты не характерны и этот расчёт выполняют, как проверочный, вычисляя контактные напряжения и сравнивая их с допускаемыми.
Расчёт зубьев на изгиб
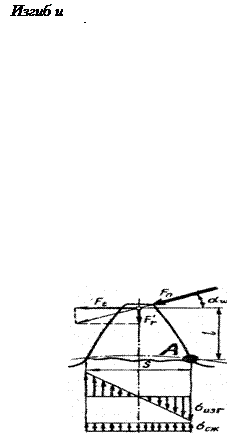Зуб представляют как консольную балку переменного сечения, нагруженную окружной и радиальной силами (изгибом от осевой силы пренебрегают). При этом окружная сила стремится изогнуть зуб, вызывая максимальные напряжения изгиба в опасном корневом сечении, а радиальная сила сжимает зуб, немного облегчая его напряжённое состояние.
s A = s изг А - s сжатия А.
Напряжения сжатия вычитаются из напряжений изгиба. Учитывая, что напряжения изгиба в консольной балке равны частному от деления изгибающего момента Mизг на момент сопротивления корневого сечения зуба W, а напряжения сжатия это сила Fr, делённая на площадь корневого сечения зуба, получаем:
.
Здесь b – ширина зуба, m – модуль зацепления, YH – коэффициент прочности зуба.
Иногда используют понятие коэффициента формы зуба YFH = 1 / YH.
Таким образом, получаем в окончательном виде условие прочности зуба на изгиб: s A = qn YH / m≤ [ s ] FE . Полученное уравнение решают, задавшись свойствами выбранного материала.
Допускаемые напряжения на изгиб (индекс F) и контактные (индекс H) зависят от свойств материала, направления приложенной нагрузки и числа циклов наработки передачи [ s ] FE = [ s ] F KF KFC / SF; [ s ] HE = [ s ] H KH / SH.
Здесь [ s ] F и [ s ] H – соответственно пределы изгибной и контактной выносливости; SF и SH – коэффициенты безопасности, зависящие от термообработки материалов; KFC учитывает влияние двухстороннего приложения нагрузки для реверсивных передач; KF и KH - коэффициенты долговечности, зависящие от соотношения фактического и базового числа циклов наработки. Фактическое число циклов наработки находится произведением частоты вращения колеса и срока его службы в минутах. Базовые числа циклов напряжений зависят от материала и термообработки зубьев.
Пример расчёта зубьев на контактную выносливость и на изгиб детально изложен в учебном пособии нашей кафедры [3].
Расчёт зубьев на изгиб для открытых передач (работают на неравномерных режимах с перегрузками) выполняют, как проектировочный. В расчёте задаются прочностными характеристиками материала и определяют модуль m, а через него и все геометрические параметры зубьев. Для закрытых передач излом зуба не характерен и этот расчёт выполняют, как проверочный, сравнивая изгибные напряжения с допускаемыми [42].
2.ПЛАНЕТАРНЫЕ ЗУБЧАТЫЕ ПЕРЕДАЧИ
Планетарными называют передачи, имеющие зубчатые колёса с перемещающимися осями. Эти подвижные колёса подобно планетам Солнечной системы вращаются вокруг своих осей и одновременно перемещаются вместе с осями, совершая плоское движение, называются они сателлитами (лат. satellitum – спутник). Подвижные колёса катятся по центральным колёсам (их иногда называют солнечными колёсами), имея с ними внешнее, а с корончатым колесом внутреннее зацепление. Оси сателлитов закреплены в водиле и вращаются вместе с ним вокруг центральной оси.
Планетарные передачи имеют ряд преимуществ перед обычными:
+ большие передаточные отношения при малых габаритах и массе;
+ возможность сложения или разложения механической мощности;
+ лёгкое управление и регулирование скорости;
+ малый шум вследствие замыкания сил в механизме.
В планетарных передачах широко применяют внутреннее зубчатое зацепление с углом aw = 30о.
Для обеспечения сборки планетарных передач необходимо соблюдать условие соосности (совпадение геометрических центров колёс); условие сборки (сумма зубьев центральных колёс кратна числу сателлитов) и соседства (вершины зубьев сателлитов не соприкасаются друг с другом).
Зубчатые колёса планетарных передач рассчитываются по тем же законам, что и колёса обычных цилиндрических передач.
3. ВОЛНОВЫЕ ЗУБЧАТЫЕ ПЕРЕДАЧИ
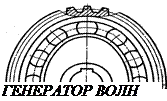Представляют собой цилиндрические передачи, где одно из колёс имеет гибкий венец. Этот гибкий венец деформируется генератором волн специальной некруглой формы и входит в зацепление с центральным колесом в двух зонах [17].
Идея волновых передач заключается в наличии нескольких пар зацепления, которые ещё и перемещаются по окружности, за счёт чего достигается огромное передаточное отношение (обычно U60 ¸ 300, известны конструкции с U > 1000). И это в одной ступени!
Принцип работы волновой передачи аналогичен работе планетарной передачи с внутренним зацеплением и деформируемым сателлитом.
Такая передача была запатентована американским инженером Массером в 1959 г.
Волновые передачи имеют меньшие массу и габариты, большую кинематическую точность, меньший мёртвый ход, высокую вибропрочность за счёт демпфирования (рассеяния энергии) колебаний, создают меньший шум.
При необходимости такие передачи позволяют передавать движение в герметичное пространство без применения уплотняющих сальников, что особенно ценно для авиационной, космической и подводной техники, а также для машин химической промышленности.
К недостаткам волновых передач относятся:
` ограниченные обороты ведущего вала (во избежание больших центробежных сил инерции некруглого генератора волн);
` мелкие модули зубьев (1,5 – 2 мм);
` практически индивидуальное, дорогостоящее, весьма трудоёмкое изготовление гибкого колеса и генератора.
Основные виды поломок волновых передач:
· разрушение подшипника генератора волн от нагрузки в зацеплении;
· проскакивание генератора волн при больших вращающих моментах, когда зубья на входе в зацепление упираются друг в друга вершинами;
· поломка гибкого колеса от трещин усталости (особенно при U < 80);
· износ зубьев на концах;
· пластические деформации боковых поверхностей зубьев при перегрузках.
Расчёт волновых зубчатых передач отличается от расчёта обычных зубчатых передач тем, что учитывается деформация гибкого венца и генератора [40].
За критерий работоспособности обычно принимают допускаемые напряжения смятия 
; 
,
где Yd – коэффициент ширины гибкого венца; d – делительный диаметр гибкого венца.
ЗАЦЕПЛЕНИЯ НОВИКОВА
Итак, основной недостаток зубчатых передач с эвольвентным профилем (цилиндрических, конических, планетарных, волновых) – высокие контактные напряжения в зубьях. Они велики потому, что контактируют два зуба с выпуклыми профилями. При этом площадка контакта очень мала, а контактные напряжения соответственно высоки. Это обстоятельство сильно ограничивает "несущую способность" передач, т.е. не позволяет передавать большие вращающие моменты.
Решая проблемы проектирования тяжёлых тихоходных машин, таких как трактора и танки, М.Л. Новиков в 1954 году разработал зацепления, в которых выпуклые зубья шестерни зацепляются с вогнутыми зубьями колеса.
К тому же выпуклый и вогнутый профили (обычно круговые) имеют близкие по абсолютной величине радиусы кривизны. За счёт этого получается большая площадка контакта, контактные напряжения уменьшаются и появляется возможность передавать примерно в 1,4 ¸ 1,8 раза большие вращающие моменты.
К сожалению, при этом приходится пожертвовать основным достоинством эвольвентных зацеплений – качением профилей зубьев друг по другу и соответственно получить высокое трение в зубьях. Однако для тихоходных машин это не так важно.
Рабочие боковые поверхности зубьев представляют собой круговинтовые поверхности, поэтому передачи можно называть круговинтовыми. В дальнейшем был разработан вариант передачи с двумя линиями зацепления.
В ней зубья каждого колеса имеют вогнутые ножки и выпуклые головки. Передачи с двумя линиями зацепления обладают большей несущей способностью, менее чувствительны к смещению осей, работают с меньшим шумом и более технологичны. Эти передачи успешно применяются при малых числах зубьев (Z1 < 10) и дают достаточную жёсткость шестерён при их большой относительной ширине.
Зацепления Новикова в редукторах применяют вместо перехода на колёса с твёрдыми поверхностями.
Расчёт передач Новикова на контактную прочность проводят на основе формулы Герца-Беляева, учитывая экспериментально установленный факт, что несущая способность передач при прочих равных условиях обратно пропорциональна синусу угла наклона зубьев. Кроме того, в расчёте немного завышаются допускаемые напряжения.
Передачи бывают однопарные, применяемые в редукторах общего назначения и многопарные, получаемые за счёт увеличения осевого размера и применяемые в прокатных станах, редукторах турбин и т.п.
4. КОНИЧЕСКИЕ ЗУБЧАТЫЕ ПЕРЕДАЧИ
Передают вращающий момент между валами с пересекающимися осями (чаще всего под углом 900). Их зубья бывают прямыми, косыми, круговыми и обычно имеют эвольвентный профиль.
И хотя, конические колёса сложнее цилиндрических как по своей геометрии, так и в изготовлении, принципы силового взаимодействия, условия работы, а следовательно, и методика расчёта аналогичны цилиндрическим.
Здесь мы рассмотрим только отличительные особенности расчёта конических колёс.
Сначала конструктор выбирает внешний окружной модуль mte, из которого рассчитывается вся геометрия зацепления, в частности, нормальный модуль в середине зуба mnm= mte (1 – 0,5 b/Re ),
где Re – внешнее конусное расстояние.
Силы в конической передаче действуют аналогично цилиндрической, однако следует помнить, что из-за перпендикулярности осей радиальная сила на шестерне аналогична осевой силе для колеса и наоборот, а окружная сила при переходе от шестерни к колесу только меняет знак
; 
.
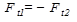Прочностные расчёты конических колёс [45] проводят аналогично цилиндрическим, по той же методике [3]. Из условия контактной выносливости определяют внешний делительный диаметр dwe, из условия прочности на изгиб находят нормальный модуль в середине зуба mnm. При этом в расчёт принимаются воображаемые эквивалентные колёса с числами зубьев Zэ1,2 =Z1,2 / cosd1,2 и диаметры dэ1,2 = mte Z1,2 / cosd1,2. Здесь Z1, Z2, - фактические числа зубьев конических колёс. При этом числа Zэ1,2 могут быть дробными.
В эквивалентных цилиндрических колёсах [32] диаметр начальной окружности и модуль соответствуют среднему сечению конического зуба, вместо межосевого расстояния берётся среднее конусное расстояние [45], а профили эквивалентных зубьев получают развёрткой дополнительного конуса на плоскость.
6. ЧЕРВЯЧНЫЕ ПЕРЕДАЧИ
Червячная передача имеет перекрещивающиеся оси валов, обычно под углом 90°. Она состоит из червяка – винта с трапецеидальной резьбой и зубчатого червячного колеса с зубьями соответствующей специфической формы.
Движение в червячной передаче преобразуется по принцпу винтовой пары. Изобретателем червячных передач считают Архимеда.
Достоинства червячных передач:
+ большое передаточное отношение (до 80);
+ плавность и бесшумность хода.
В отличие от эвольвентных зацеплений, где преобладает контактное качение, виток червяка скользит по зубу колеса. Следовательно, червячные передачи имеют "по определению" один фундаментальный недостаток: высокое трение в зацеплении. Это ведёт к низкому КПД (на 20-30% ниже, чем у зубчатых), износу, нагреву и необходимости применять дорогие антифрикционные материалы.
Кроме того, помимо достоинств и недостатков, червячные передачи имеют важное свойство: движение передаётся только от червяка к колесу, а не наоборот. Никакой вращающий момент, приложенный к колесу, не заставит вращаться червяк. Именно поэтому червячные передачи находят применение в подъёмных механизмах, например в лифтах. Там электродвигатель соединён с червяком, а трос пассажирской кабины намотан на вал червячного колеса во избежание самопроизвольного опускания или падения.
Это свойство не надо путать с реверсивностью механизма. Ведь направление вращения червяка может быть любым, приводя либо к подъёму, либо к спуску той же лифтовой кабины.
Передаточное отношение червячной передачи находят аналогично цилиндрической U = n1 / n2 = Z2 / Z1.
Здесь Z2 – число зубьев колеса, а роль числа зубьев шестерни Z1 выполняет число заходов червяка, которое обычно бывает равно 1, 2, 3 или 4.
Очевидно, что однозаходный червяк даёт наибольшее передаточное отношение, однако наивысший КПД достигается при многозаходных червяках, что связано с уменьшением трения за счёт роста угла трения.
Основные причины выхода из строя червячных передач:
r поверхностное выкрашивание и схватывание;
r излом зуба.
Это напоминает характерные дефекты зубчатых передач, поэтому и расчёты проводятся аналогично [44].
В осевом сечении червячная пара фактически представляет собой прямобочное реечное зацепление, где радиус кривизны боковой поверхности "рейки" (винта червяка) r1 равен бесконечности и, следовательно, приведённый радиус кривизны равен радиусу кривизны зуба колеса
rпр = r2.
Далее расчёт проводится по формуле Герца-Беляева. Из проектировочного расчёта находят осевой модуль червяка, а по нему и все геометрические параметры зацепления.
Особенность расчёта на изгиб состоит в том, что принимается эквивалентное число зубьев Zэкв = Z2 / cos3g, где g - угол подъёма витков червяка.
Вследствие нагрева, вызванного трением, червячные передачи нуждаются также и в тепловом расчёте. Практика показывает, что механизм опасно нагревать выше 95оС. Допускаемая температура назначается 65 oC.
Уравнение для теплового расчёта составляется из баланса тепловой энергии, а именно: выделяемое червячной парой тепло должно полностью отводиться в окружающую среду
Qвыделяемое = Qотводимое.
Решая это уравнение, находим температуру редуктора, передающего заданную мощность N
t = [ 860 N (1- η )] / [ KT S (1- Ψ )] + to.
где KT – коэффициент теплоотдачи, S – поверхность охлаждения (корпус), to – температура окружающей среды, Y – коэффициент теплоотвода в пол.
В случае, когда расчётная температура превышает допускаемую, то следует предусмотреть отвод избыточной теплоты. Это достигается оребрением редуктора, искусственной вентиляцией, змеевиками с охлаждающей жидкостью в масляной ванне и т.д.
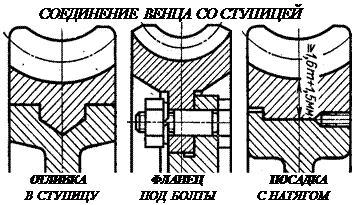Оптимальная пара трения это "сталь по бронзе". Поэтому при стальном червяке червячные колёса должны выполняться из бронзовых сплавов. Однако цветные металлы дороги и поэтому из бронзы выполняется лишь зубчатый венец, который крепится на сравнительно дешёвой стальной ступице. Таким образом, червячное колесо - сборочная единица, где самые популярные способы крепления венца это либо центробежное литьё в кольцевую канавку ступицы; либо крепление венца к ступице болтами за фланец; либо посадка с натягом и стопорение винтами для предотвращения взаимного смещения венца и ступицы.
Крепление венца к ступице должно обеспечивать фиксацию как от проворота (осевая сила червяка = окружной силе колеса), так и от осевого "снятия" венца (окружная сила червяка = осевой силе колеса).
КОНТРОЛЬНЫЕ ВОПРОСЫ
s Каково назначение передач в машинах?
s Каковы области применения прямозубых и косозубых передач?
s Каковы сравнительные достоинства прямозубых и косозубых колёс?
s Как определяется передаточное отношение и передаточное число?
s Каковы главные виды разрушений зубчатых колёс?
s Какие силы действуют в зубчатом зацеплении?
s Какие допущения принимаются при расчёте зубьев на контактную прочность?
s По какой расчётной схеме выполняется расчёт зубьев на изгиб?
s В чём заключаются достоинства и недостатки планетарных передач?
s Для чего созданы волновые передачи и в чём заключается принцип их работы?
s В чём заключаются достоинства и недостатки волновых передач?
s Для чего созданы зацепления Новикова и в чём заключается принцип конструкции их зубьев?
s В чём заключаются достоинства и недостатки зацеплений Новикова?
s В чём заключается принцип конструкции червячной передачи?
s Каковы достоинства и недостатки червячных передач?
s Какое свойство червячной передачи отличает её от других передач?
s Каковы основные причины поломок червячных передач?
s Из каких условий находят температуру червячной передачи?
s Какие методы могут применяться для снижения температуры червячной передачи?
s Какие материалы должны применяться для червячной передачи?
s Каковы особенности конструкции червячных колёс?
Поиск по сайту: