Аллен Карр

Я хочу поделиться с вами историей, свидетелем которой я стал пару месяцев назад. Окна квартиры, где я живу, выходят на детскую площадку. И когда было потеплее, мамы со своими детьми каждый день гуляли во дворе. Я обожаю наблюдать за детьми. Вот уж где кладезь мудрости. И однажды один из этих детей открыл мне великое знание.

Маленький мальчик, трех лет от роду, отошел от игровой площадки к парковке и за чем-то внимательно наблюдал. В какой-то момент его мама увидела, что он ушел слишком далеко, и побежала к нему, выкрикивая его имя. Надо сказать, она была очень испугана. Ее можно понять, так как за парковкой начинается дорога, по которой постоянно едут автомобили и, если ребенок выбежит, его могут не заметить и тогда случится катастрофа.

Но ребенок мирно стоял, что-то с интересом разглядывая под машиной. Тут подбегает истеричная мамаша и вместо того, чтобы узнать у сына, что же он такого интересного увидел, хватает его за руку и силой начинает оттаскивать от машины. Пацан сопротивляется что есть мочи, он явно хочет продолжить свое исследование мира. Маме это по фигу, она хорошенько шлепает по попе малыша и, убедившись, что он на безопасном расстоянии от дороги, оставляет его рядом с велосипедом и идет к скамейке.

Что делает пацан? Он садится на свой трехколесный велик, разгоняется и на всей скорости берет маму на таран. Да, он просто врезается ей в ноги. Мама разворачивается, что-то говорит ему, глядя сверху вниз, и идет дальше. Ребенок слезает с велосипеда, догоняет маму и начинает обнимать ее за ногу.

Казалось бы, рядовая история. Но как же много она показала…

Во-первых, исследование ребенка есть не что иное, как порыв его мужского начала. Что вообще такое мужское/женское начало? Это место, где начинается мое «Я». Мое подлинное «Я». Одно дело, когда мама говорит пойти поиграть в песочнице, а другое - когда я сам принимаю решение, что мне делать. И вот этот мальчик что-то увидел. Его начало заинтересовалось находкой, и он испытал порыв исследовать мир. Его Дух начал проявлять себя через это начинание.

Перепуганная собственными мыслями мама стала оттаскивать его в сторону и ругать за то, что он ее ослушался. Ребенок же воспринял это как подавление собственного Духа, отсюда реакция в виде попытки протаранить маму на велосипеде. Он просто защищал свое право САМОСТОЯТЕЛЬНО исследовать мир. Но мама что-то сказала ему, вызвав чувство вины. Дух ребенка сдался, и пацан побежал просить прощения у мамы.

Я представил этого мальчика через много лет. Вот он уже женат, имеет собственных детей. И у него возникает желание пойти с друзьями в бар - посмотреть футбол или что-то вроде того. И в этот же момент он вспоминает, что дома супруга совсем одна. И он испытает чувство вины. Он не поймет почему, ведь ситуацию из детства он забудет.

Ему вложили в голову, что самостоятельные решения в жизни вызывают чувство вины. И быть может, жена была бы и не против, чтобы муж отдохнул с друзьями, но он чувствует вину уже за саму мысль о том, что может обидеть ее.

К чему я это все? Присмотритесь к себе. В нас так мало нас настоящих. Наше поведение - это просто череда комплексов, которые мы все время пытаемся компенсировать. Мы ходим на работу, которую не любим, живем с людьми, которых не любим, делаем то, что хотят другие. Но где в этом наше «Я»? В том, что я делаю, в том, что я чувствую, есть «Я»? «Я» хоть где-то есть?

Осознайте простую истину. Ваша жизнь - только ваша. Возьмите ответственность за нее и начните САМИ решать, что в ней главное. Пусть ваше «Я» заявит о себе на весь мир. Многие отвернутся от вас. Но вы будете чувствовать себя по-настоящему счастливыми.

В конце хотелось бы процитировать одного уже взрослого мужика. И именно в тот момент, когда он осознал то, о чем пишет, он начал взрослеть.

«И я понял в этот момент, по кому скучаю. Я понял, какого человека мне не хватает в жизни. Я со всей ясностью осознал, по кому я невыносимо тоскую, тоскую давно, и кого мне так недостает каждый прожитый мною день. Это конкретный человек. Я скучаю по себе. Счастливому!»

Евгений Гришковец

Рис.1

Если маятник из положения равновесия отклонили на некоторый угол α, то, используя уравнение динамики вращательного движения твердого тела, момент M возвращающей силы

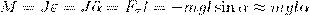(4)

где J — момент инерции маятника относительно оси, которая проходит через точку подвеса О, l – расстояние между осью и центром масс маятника, F_τ ≈ –mgsinα ≈ –mgα — возвращающая сила (знак минус указывает на то, что направления F_τ и α всегда противоположны; sinα ≈ α поскольку колебания маятника считаются малыми, т.е. маятника из положения равновесия отклоняется на малые углы). Уравнение (4) запишем как

или

Принимая

(5)

получим уравнение

идентичное с (1), решение которого (1) найдем и запишем как:

(6)

Из формулы (6) вытекает, что при малых колебаниях физический маятник совершает гармонические колебания с циклической частотой ω₀ и периодом

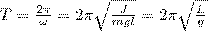(7)

где введена величина L=J/(m l) — приведенная длина физического маятника.

Точка О' на продолжении прямой ОС, которая отстоит от точки О подвеса маятника на расстоянии приведенной длины L, называется центром качаний физического маятника (рис. 1). Применяя теорему Штейнера для момента инерции оси, найдем

т. е. ОО' всегда больше ОС. Точка подвеса О маятника и центр качаний О' имеют свойство взаимозаменяемости: если точку подвеса перенести в центр качаний, то прежняя точка О подвеса будет новым центром качаний, и при этом не изменится период колебаний физического маятника.

3. Математический маятник — это идеализированная система, состоящая из материальной точки массой m, которая подвешена на нерастяжимой невесомой нити, и которая колеблется под действием силы тяжести. Хорошее приближение математического маятника есть небольшой тяжелый шарик, который подвешен на длинной тонкой нити. Момент инерции математического маятника

(8)

где l — длина маятника.

Поскольку математический маятник есть частный случай физического маятника, если предположить, что вся его масса сосредоточена в одной точке — центре масс, то, подставив (8) в (7), найдем выражение для периода малых колебаний математического маятника

(9)

Сопоставляя формулы (7) и (9), видим, что если приведенная длина L физического маятника равна длине l математического маятника, то периоды колебаний этих маятников одинаковы. Значит, приведенная длина физического маятника — это длина такого математического маятника, у которого период колебаний совпадает с периодом колебаний данного физического маятника.

4 Енергiя гармонiчних коливань

Під час гармонічного коливального руху кінетична енергія коливальної системи і потенціальна енергія взаємодії невпинно змінюються.

Повна енергія коливального руху:

; ,

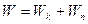поскільки .

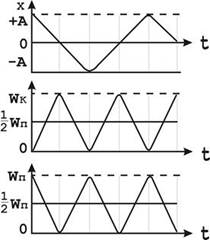
Кінетична енергія змінюється за гармонічним законом, але з подвоєнною частотою.

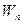кількісно дорівнює роботі квазіпружньої сили ;

;

;

.

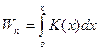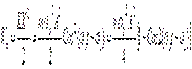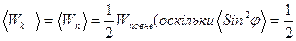Потенціальна енергія 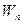змінюється як і кінетична енергія, з частотою 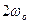і в тиж же межах від 0 до 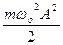, але зі зсувом фаз відносно кінетичної енергії на p.

5.Складання гармонiчних коливань одного напрямку i однiеi частоти. Биття.

Розглянемо додавання двох коливань однакового напрямку з однаковими періодами, які відбуваються з деякою різницею фаз і мають різні амплітуди. Нехай ці коливання відбуваються в напрямі осі x. Запишемо рівняння цих коливань

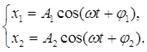(1)

Циклічні частоти ω в обох випадках однакові. Зміщення x від положення рівноваги, при участі тіла одночасно в двох коливаннях, виражається алгебраїчною сумою

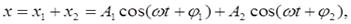
Або

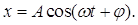(2)

Для знаходження результуючої амплітуди А і початкової фази результуючого коливання φ використаємо векторну діаграму (рис.1).

Так-як вектори 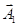і 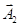обертаються з однаковою циклічною частотою ω, то різниця фаз 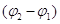між ними залишається постійною. Результуючу амплітуду А в цьому випадку визначають за теоремою косинусів, тобто

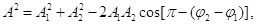(3)

або з урахуванням того, що одержуємо:

Рис.1

(4)

і

(5)

Початкова фаза результуючого коливання φ дорівнює

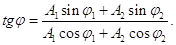(6)

Значення амплітуди (5) і початкової фази (6) підставимо в рівняння (2), одержимо

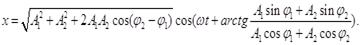(7)

Як видно з (7), сумарне коливання має такий же напрям і відбувається з тією ж циклічною частотою ω. Амплітуда результуючого коливання залежить від різниці фаз обох коливань.

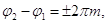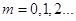Якщо де (), то ;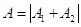

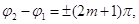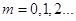Якщо де (), то .

Оскільки 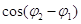може набувати значень від –1 до +1, то межі зміни амплітуди будуть такими:

(8)

Окремим випадком можна розглядати додавання коливань з близькими циклічними частотами 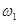і 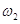(). Періодична зміна амплітуди з часом, яка відбувається в цьому випадку, називається биттям. Нехай додаються два гармонічних коливання з амплітудами 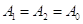і близькими циклічними частотами 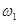і 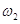. Початкові фази таких гармонічних коливань можна вибрати однаковими, тому

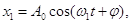(9)

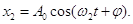(10)

Різниця фаз двох коливань (9) і (10) буде дорівнювати .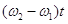

Скористаємось теоремою косинусів для визначення амплітуди биття

(11)

Замінимо вираз в квадратних дужках у відповідності з формулою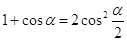

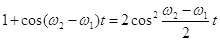(12)

Вираз (12) підставимо в (11)

. (13)

або

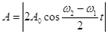(14)

Фаза результуючого коливання для довільного проміжку часу знаходиться із графіка (рис.2)

(15)

Результуюче коливання биття матиме вигляд:

(16)

де – амплітуда биття.

Рис.2

Графік залежності (16) має вигляд (рис 3):

Періодичність зміни амплітуди від максимуму до максимуму дає час, який називається періодом биття

, звідки (17)

Періодичність зміни амплітуди високочастотних коливань визначається за формулою

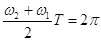, звідки 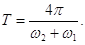(18)

Оскільки циклічні частоти досить близькі, то наближено

(19)

За час 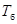відбувається n гармонічних високочастотних коливань, тому

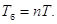(20)

З урахуванням співвідношень (17) і (19) вираз (20) перепишеться

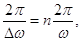(21)

звідки 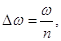а для частот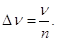

В процесі биття частоти генераторів визначаються в таких межах:

(22)

Биття використовується для вимірювання частоти невідомого генератора в процесі їх виготовлення. Складання однаково направлених коливань забезпечує амплітудну модуляцію в радіотехніці, а також проміжну частоту супергетеродинного прийому радіо і телепередач.

Аллен Карр

Поиск по сайту: